手把手教你玩转傅立叶变换——原理与代码

本帖最后由 9crk 于 2016-7-19 09:52 编辑

傅里叶变换：即将时间上的采样数据变成频率分布数据。
快速傅里叶变换：傅里叶变换出现多年之后，人们才发现的一种加快傅里叶变换的方法、
傅里叶变换的原理：
              如果一个sin(3x)信号与一个sin(3x)信号相乘（想象成两条扭曲的彩带，两条彩带上面的每个点进行乘法运算），把结果进行累加，则会得到一个比较大的值，而一个sin(3x)与sin(4x)相乘，结果进行累加，则会比较小。
             按照这个特点，就可以将时间域的数据转成频率域。
             而很多时候，我们并不知道这个信号是不是跟sin(3x)同相位的，它有可能频率与sin(3x)相同，但存在相位差，比如sin(3(x+0.4))，这个时候，怎么办呢？拿多少度的相位差公式去跟这个信号相乘呢？

             勤劳的人们发现，sin和cos两个函数是正交的，如果相位不同，在跟sin相乘损失的量可以在cos上补回来，就是说
             A = sin(3x) * sin(3(x+0.4)) + cos(3x)*sin(3(x+0.4)) --------------------------（式1）
            sqrt(A)即可得到这个频率的幅值信息，不管相位是多少。
            
因此，如果我采集了一个位置信号S[0:1000]
我要计算1 4 8三个频率的幅值，就可以构造sin(1x)  sin(4x) sin(8x)  cos(1x) cos(4x) cos(8x)这6个信号出来，然后按照（式1）操作，就可以得到幅值。
同理，我可以计算从1到500的频率幅度各为多少。（为什么只能计算到500？因为至少两点决定一个频率，总共才1000点）

至此，傅里叶变换原理完结。而快速傅里叶变换，只是去掉了冗余的步骤，让计算更简便。计算结构如下图所示：【不需要去理解这个结构】



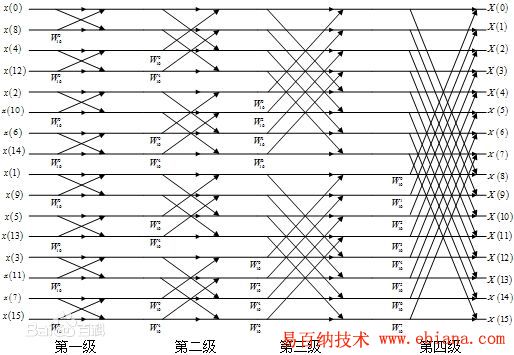
代码如下：
[code]#include
#include
#define PI 3.1415926535897932384626433832795028841971 //定义圆周率值
#define FFT_N 128 //定义福利叶变换的点数
struct compx {double real,imag;}; //定义一个复数结构
struct compx s[FFT_N]; //FFT输入和输出：从S[1]开始存放，根据大小自己定义

/*******************************************************************
函数原型：struct compx EE(struct compx b1,struct compx b2)
函数功能：对两个复数进行乘法运算
输入参数：两个以联合体定义的复数a,b
输出参数：a和b的乘积，以联合体的形式输出
*******************************************************************/
struct compx EE(struct compx a,struct compx b)
{
struct compx c;
c.real=a.real*b.real-a.imag*b.imag;
c.imag=a.real*b.imag+a.imag*b.real;
return(c);
}
/*****************************************************************
函数原型：void FFT(struct compx *xin,int N)
函数功能：对输入的复数组进行快速傅里叶变换（FFT）
输入参数：*xin复数结构体组的首地址指针，struct型
*****************************************************************/
void FFT(struct compx *xin)
{
int f,m,nv2,nm1,i,k,l,j=0;
struct compx u,w,t;

//变址运算，即把自然顺序变成倒位序，采用雷德算法
nv2=FFT_N/2;
nm1=FFT_N-1;
for(i=0;i {
if(i {
t=xin[j];
xin[j]=xin;
xin=t;
}
k=nv2; //求j的下一个倒位序
while(k<=j) //如果k<=j,表示j的最高位为1
{
j=j-k; //把最高位变成0
k=k/2; //k/2，比较次高位，依次类推，逐个比较，直到某个位为0
}
j=j+k; //把0改为1
}
//三重交换蝶形运算

{
int le,lei,ip; //FFT运算核，使用蝶形运算完成FFT运算
f=FFT_N;
for(l=1;(f=f/2)!=1;l++) //计算l的值，即计算蝶形级数
;
for(m=1;m<=l;m++) // 控制蝶形结级数
{ //m表示第m级蝶形，l为蝶形级总数l=log（2）N
le=2<<(m-1); //le蝶形结距离，即第m级蝶形的蝶形结相距le点
lei=le/2; //同一蝶形结中参加运算的两点的距离
u.real=1.0; //u为蝶形结运算系数，初始值为1
u.imag=0.0;
w.real=cos(PI/lei); //w为系数商，即当前系数与前一个系数的商
w.imag=-sin(PI/lei);
for(j=0;j<=lei-1;j++) //控制计算不同种蝶形结，即计算系数不同的蝶形结
{
for(i=j;i<=FFT_N-1;i=i+le) //控制同一蝶形结运算，即计算系数相同蝶形结
{
ip=i+lei; //i，ip分别表示参加蝶形运算的两个节点
t=EE(xin[ip],u); //蝶形运算，详见公式
xin[ip].real=xin.real-t.real;
xin[ip].imag=xin.imag-t.imag;
xin.real=xin.real+t.real;
xin.imag=xin.imag+t.imag;
}
u=EE(u,w); //改变系数，进行下一个蝶形运算
}
}
}

}
/************************************************************
函数原型：void main()
函数功能：测试FFT变换，演示函数使用方法
输入参数：无
输出参数：无
************************************************************/
void main()
{
int i;
//产生一个信号sin(n*2*PI*i/FFT_N)，放在实部
for(i=0;i {
s.real=sin(11*2*PI*i/FFT_N);
s.imag=0; //虚部为0
}

FFT(s); //进行快速福利叶变换
//变换后的值需要开根号
for(i=0;i s.real=sqrt(s.real*s.real+s.imag*s.imag);
//显示出来
for(i=0;i printf("%d Hz:\t%f\n",i,s.real);
}[/code]

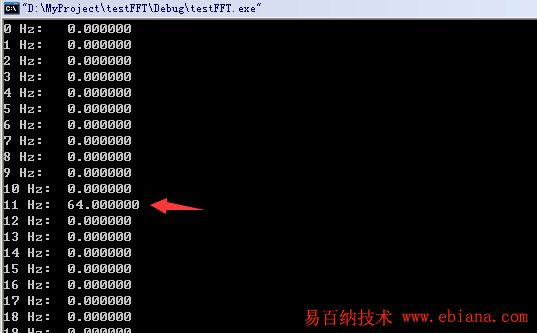
如果你觉得这个效果非常好，很给力，那么请尝试将信号源[code]s.real=sin(11*2*PI*i/FFT_N)[/code]改成[code]s.real=sin(11.5*2*PI*i/FFT_N); [/code]
没错，改成11.5，未知信号嘛，随便是多少，很任性。
结果如下：

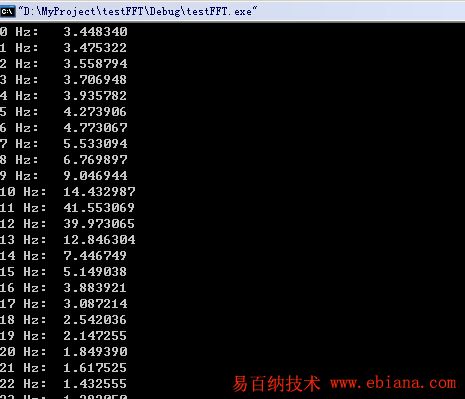
很不幸，这就叫频谱泄露。原因是由于计算机只能处理离散信号（就是只能1 2 3 4 5，而不能从1.11111111无数个1到4.9999999999999无数个9），当频率不是整数倍时，就会泄露到整个频域。
那么，这个时候，窗函数就应运而生了！

下面贴出我加了窗后的效果：

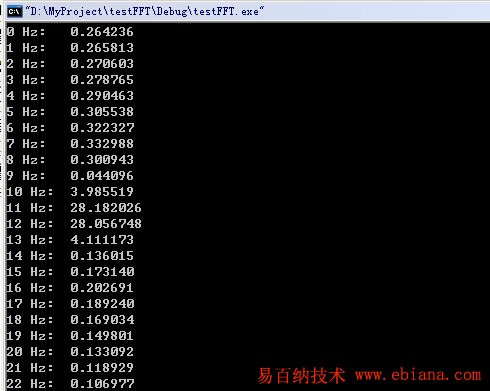
是不是效果非常好！
怎样加窗呢？下面贴出修改后的main函数
[code]void main()
{
int i;
//产生一个信号sin(n*2*PI*i/FFT_N)，放在实部
for(i=0;i {
s.real=sin(11.5*2*PI*i/FFT_N);
s.imag=0; //虚部为0
}
for(i=0;i {
s.real=s.real*(0.54-0.46*cos(2*i*PI/(FFT_N-1)));
}
FFT(s); //进行快速福利叶变换
//变换后的值需要开根号
for(i=0;i s.real=sqrt(s.real*s.real+s.imag*s.imag);
//显示出来
for(i=0;i printf("%d Hz:\t%f\n",i,s.real);
} [/code]

其实就是增加了
for(i=0;i {
         s.real=s.real*(0.54-0.46*cos(2*i*PI/(FFT_N-1)));
}
这一句
这是一个……不记得叫什么窗了
常用的有汉宁窗、海明窗、三角窗……各种窗。
各种不一样的窗有不一样的用途。
主要的差异是“旁瓣窄主瓣宽”还是“旁瓣宽主瓣窄”
比如下图中两个


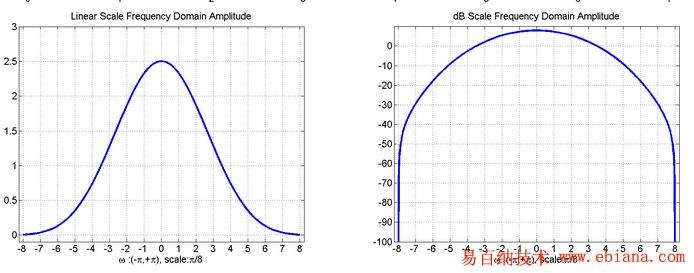
比如左边的，由于两边往下压太多，就会导致幅度不真实，但由于中间凸起，就导致了频率高的部分很尖锐，这种窗适合分析频点的具体位置。

比如右边的窗，比较胖，基本保留了原来的所有信息，所以适合用于幅值的分析，但频点就不好分析了，因为可能4Hz和5Hz就挨着很近，都不知道到底是4还是5还是4.5……

好吧，FFT的所有技术都在这里了。。。欢迎交流。

本文原创，转载请注明作者：9crk :lol