基于深度学习和神经网络的重要基础及方法概要

这是深度学习和神经网络的初学者指南。本文将讨论深度学习和神经网络的含义。特别是，这里将专注于深度学习在一些实践中的应用。

深度学习到底是什么？

您是否曾经想过Google的翻译器应用程序如何在几毫秒内将整个段落从一种语言翻译成另一种语言？

Netflix和YouTube如何确定我们在电影或视频中的品味并提供适当的建议？

甚至自动驾驶汽车又怎么可能做到驾驶建议？

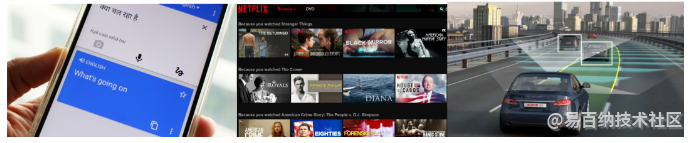
所有得这些都是深度学习和人工神经网络的产品。深度学习和神经网络的定义将在下面介绍。让我们首先从深度学习的定义开始。深度学习是机器学习的子集，而另一方面，机器学习是人工智能的子集。人工智能是一个通用术语，指的是使计算机能够模仿人类行为的技术。机器学习表示在数据上训练的一组算法，这些使所有这些成为可能。

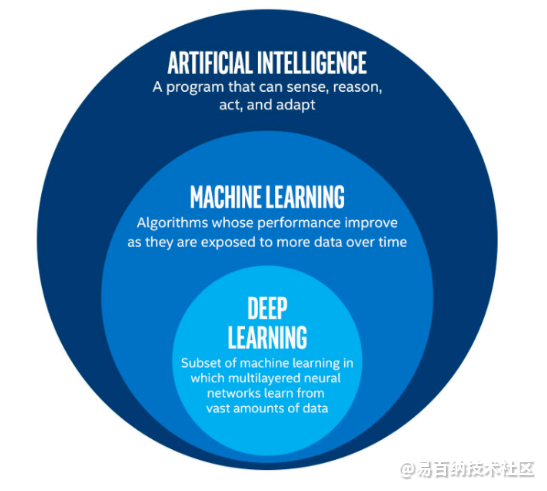
AI与ML与DL

另一方面，深度学习只是受人脑结构启发的一种机器学习。深度学习算法试图通过不断分析具有给定逻辑结构的数据来得出与人类相似的结论。为此，深度学习使用称为神经网络的算法的多层结构。

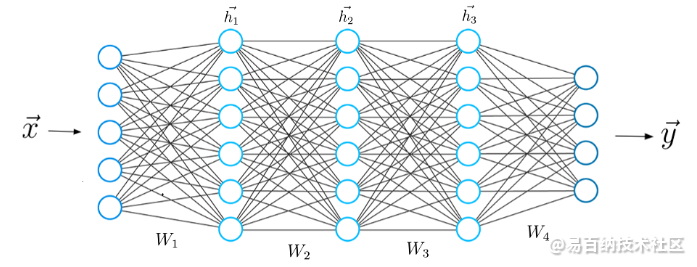
典型的神经网络

神经网络的设计基于人脑的结构。就像我们使用大脑来识别模式并分类不同类型的信息一样，可以教会神经网络对数据执行相同的任务。

神经网络的各个层也可以被认为是一种过滤器，其作用范围从整体到微小，都增加了检测和输出正确结果的可能性。

人脑的工作与此类似。每当我们收到新信息时，大脑都会尝试将其与已知对象进行比较。深度神经网络也使用相同的概念。

神经网络使我们能够执行许多任务，例如聚类，分类或回归。使用神经网络，我们可以根据数据中样本之间的相似性对未标记的数据进行分组或排序。或者在分类的情况下，我们可以在标记的数据集上训练网络，以便将该数据集中的样本分类为不同的类别。

通常，神经网络可以执行与经典机器学习算法相同的任务。但是，事实并非如此。

人工神经网络具有独特的功能，使深度学习模型能够解决机器学习模型无法解决的任务。

为什么深度学习如此受欢迎？

近年来，人工智能的所有最新进展都归因于深度学习。没有深度学习，我们就不会有自动驾驶汽车，聊天机器人或Alexa和Siri这样的私人助手。Google翻译应用程序将继续像10年前一样原始（在Google切换到该应用程序的神经网络之前），而Netflix或Youtube不知道我们喜欢还是不喜欢哪部电影或电视连续剧。所有这些技术的背后都是神经网络。

我们甚至可以说，在人工神经网络和深度学习的推动下，今天正在发生一场新的工业革命。

归根结底，深度学习是到目前为止我们对真实机器智能的最好的，最明显的方法。

为什么深度学习和人工神经网络在当今行业如此强大和独特？最重要的是，为什么深度学习模型比机器学习模型更强大？下面向您解释。

相比机器学习，深度学习的第一个优势是所谓的特征提取是不必要的。

在使用深度学习之前，很早就开始使用传统的机器学习方法。例如决策树，SVM，朴素贝叶斯分类器和逻辑回归。

这些算法也称为平面算法。这里的平面表示这些算法通常不能直接应用于原始数据（例如.csv，图像，文本等）。我们需要一个称为特征提取的预处理步骤。

特征提取的结果是给定原始数据存在的规律进行的表示，这些原始数据现在可以被这些经典的机器学习算法用来执行任务。例如，将数据分类为几个类别。

特征提取通常非常复杂，并且需要详细的统计和复杂网络知识。为了获得最 佳结果，必须对该预处理层进行多次调整，测试和完善。

另一方面是深度学习的人工神经网络门类，这些门类不需要特征提取步骤。

此外，这些神经网络层能够直接或独立地学习原始数据的隐式表示。在这里，原始数据越来越抽象和压缩的表示在人工神经网络的多层上的产生方式。输入数据的这种压缩表示会被用于产生结果，而该结果如同将输入数据分类为不同的类别。

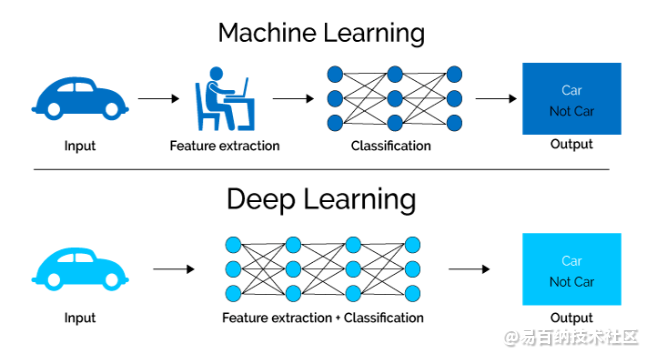
仅ML算法才需要特征提取

换句话说，我们也可以说特征提取步骤已经是属于人工神经网络中进行的过程的一部分。

在训练过程中，神经网络还优化了此步骤，以获得输入数据的最 佳可能抽象表示。因此，这意味着深度学习的模型几乎不需要或不需要人工来执行和优化特征提取过程。

下面来看一个具体的例子。例如，如果您想使用机器学习模型来确定特定图像是否在显示汽车，我们人类首先需要确定汽车是汽车的独特特征（例如：汽车的形状，大小，窗户，车轮等），提取这些特征并将其作为输入数据提供给算法。

这样，算法将对图像进行分类。也就是说，在机器学习中，工程师必须直接干预动作才能得出模型结论。

在深度学习模型的情况下，完全不需要特征提取步骤。该模型将识别汽车的这些独特的特征并做出正确的预测。

这就完全没有人类的帮助!

实际上，避免提取数据特征适用于您将使用神经网络执行的所有其他任务。只要将原始数据提供给神经网络，其余的就由模型完成。

大数据时代…深度学习的第二个巨大优势，以及了解深度学习为何如此受欢迎的关键部分是它由海量数据提供支持。技术的“大数据时代”将为深度学习新的创新提供大量机会。根据中国主要搜索引擎百度的首席科学家，谷歌大脑项目的负责人之一吴安德说，“ 与深度学习的类比是，火箭引擎是深度学习模型，而燃料是我们可以馈送到这些算法的大量数据。”

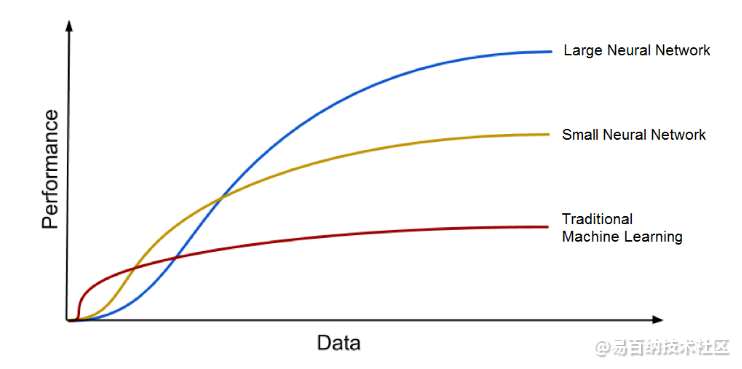
深度学习算法随着数据量的增加而变得更好

深度学习模型倾向于随着训练数据量的增加而提高其准确性，传统的机器学习模型（例如SVM和Naive Bayes分类器）在达到饱和点后就停止改善。

生物神经网络

在我们进一步使用人工神经网络之前，这里介绍一下生物神经网络背后的概念，因此当讨论人工神经网络时，我们可以看到与生物学模型的相似之处。

人工神经网络的灵感来自大脑中的生物神经元。实际上，人工神经网络以非常简单的方式模拟了我们大脑中神经网络的一些基本功能。首先让我们看一下生物神经网络，以得出与人工神经网络相似的东西。简而言之，生物神经网络由众多神经元组成。

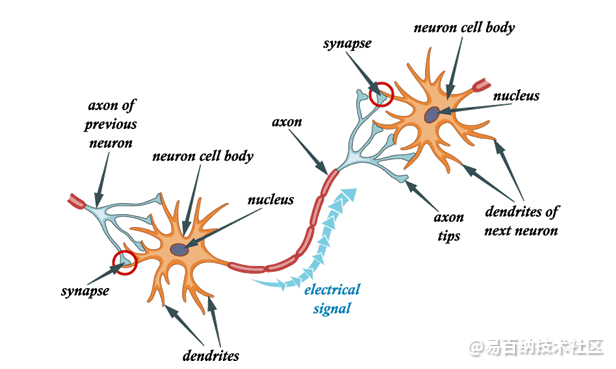
生物神经网络模型

典型的神经元由细胞体，树突和轴突组成。树突是从细胞体内出来的薄结构。轴突是从该细胞体中出现的细胞延伸。大多数神经元通过树突接收信号，并沿轴突发出信号。

在大多数突触中，信号从一个神经元的轴突穿越到另一个神经元的树突。由于维持其膜中的电压梯度，所有神经元均具有电兴奋性。如果电压在很短的间隔内变化足够大，则神经元会生成称为动作电位的电化学脉冲。该电位沿轴突快速传播，并在到达突触时激活突触连接。

人工神经网络

现在我们对生物神经网络的功能有了基本的了解，让我们看一下人工神经网络的体系结构。

神经网络通常由一组连接的单元或节点组成。我们称这些节点为神经元。这些人工神经元松散地模拟了我们大脑的生物神经元。

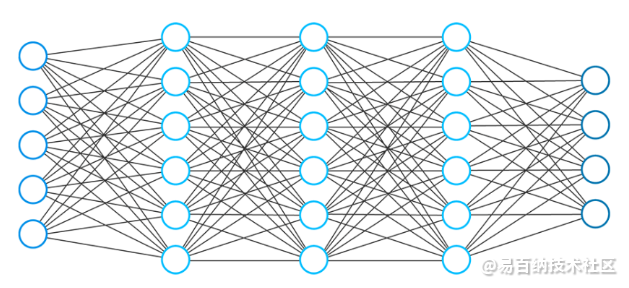
人工前馈神经网络

神经元用数字值（例如1.2、5.0、42.0、0.25等）的图形表示。两个人工神经元之间的任何连接都可以视为真实生物大脑中的轴突。

神经元之间的连接是通过所谓的权重实现的，这些权重也不过是数值。

当人工神经网络学习时，神经元之间的权重会发生变化，连接强度也会改变。含义：给定训练数据和特定任务（例如，数字分类），我们正在寻找允许神经网络执行某些确定的权重分类。如果每个任务和每个数据集的权重集都不同，我们无法预先预测这些权重的值，但是神经网络必须学习它们，学习的这一过程也称为培训。

神经网络架构

我们称第一层为输入层，输入层接收输入x，即神经网络从中学习的数据。在我们之前的手写数字分类示例中深度学习基础4：Tensorflow2.0数据集与神经网络的初探，这些输入x将代表这些数字的图像（x基本上是整个矢量，其中每个条目都是一个像素）。

输入层具有与向量x中相同的神经元数量。含义：每个输入神经元代表向量x中的一个元素。

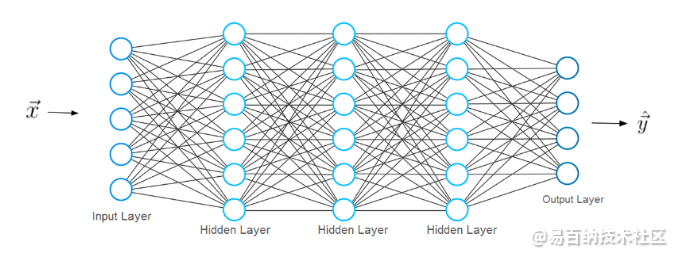
前馈神经网络的结构

最后一层称为输出层，输出层输出向量y，表示神经网络产生的结果。此向量中的条目表示输出层中神经元的值。在分类的情况下，最后一层的每个神经元将代表不同的类别。

在这种情况下，输出神经元的值给出了特征x给出的手写数字属于一种可能类别（数字0–9之一）的可能性。可以想象，输出神经元的数量必须与类相同。

为了获得预测向量y，网络必须执行某些数学运算。这些操作在输入和输出层之间的层中执行。我们称这些层为隐藏层。现在让我们讨论各层之间的连接如何。

层连接

下面考虑一个仅由两层组成的神经网络的较小示例。输入层具有两个输入神经元，而输出层则包含三个神经元。

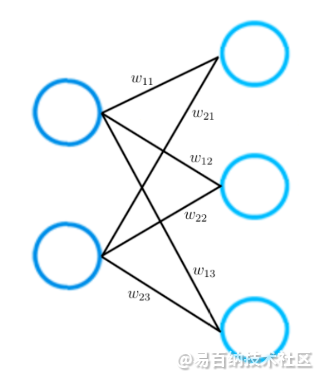
层连接

如以上所述：两个神经元之间的每个连接都由一个数值表示，我们称它为权重。

如图所示，两个神经元之间的每个连接都由不同的权重w表示。这些权重w中的每一个具有的索引值，这些索引的第一个值表示用来连接所源自的层中神经元的数量，第二个值表示连接所导致的层中神经元的数量。

两个神经网络层之间的所有权重都可以由称为权重矩阵的矩阵表示。

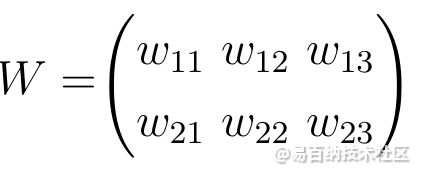
权重矩阵

权重矩阵的条目数与神经元之间的连接数相同。权重矩阵的尺寸由通过该权重矩阵连接的两层的大小得出。

行数对应于连接所源自的层中神经元的数量；

列数对应于连接所导致的层中神经元的数量。

在此特定示例中，权重矩阵的行数对应于输入层的大小为2，而列数对应于输出层的大小为3。

神经网络中的学习过程

现在我们更好地了解了神经网络架构，我们可以直观地学习神经网络的学习过程。让我们一步一步地做。通过上述，您已经知道第一步：对于给定的输入特征向量x，神经网络计算一个预测向量，在这里我们称之为h。

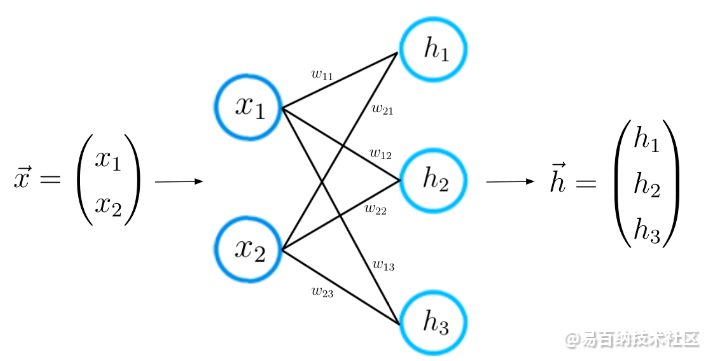
正向传播

此步骤也称为正向传播。使用输入向量x和连接两个神经元层的权重矩阵W，我们计算向量x和矩阵W之间的点积。这个点积的结果还是一个向量，我们称之为

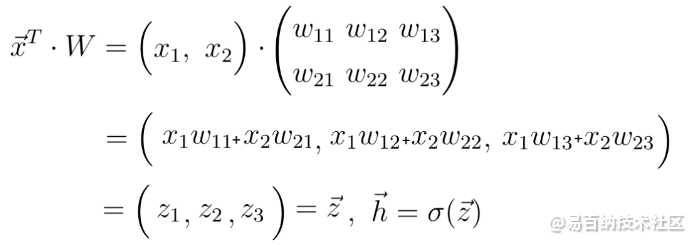
正向传播方程

ž通过将所谓的激活函数应用于向量z来获得最终预测向量h。在这种情况下，激活函数由字母Sigma表示。激活函数只是执行从z到h的非线性映射的非线性函数。

在这一点上，您可能会认识到神经网络中神经元背后的含义：神经元只是数字值的表示。

让我们仔细看一下向量z。如您所见，z的每个元素都由输入向量x组成。此时，砝码的作用得以完美展现。一层中的神经元值由上一层神经元值的线性组合组成，这些线性值由一些数值加权。

这些数值是权重，告诉我们这些神经元之间的相互连接程度。

在训练过程中，这些权重被调整，一些神经元变得更紧密，某些神经元变得更稀疏。就像在生物神经网络中一样，学习意味着权重的改变。因此，z，h和最终输出向量y的值随权重而变化。一些权重使我们对神经网络的预测更接近实际的地面真实向量y_hat，一些权重增加了与地面真实向量的距离。

现在我们知道了两个神经网络层之间的数学计算是什么样子，我们可以将知识扩展到一个由5层组成的更深层次的体系结构。

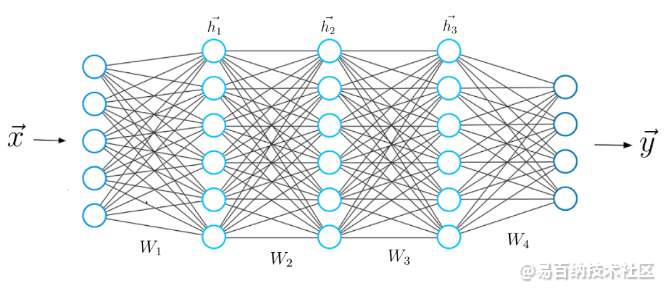
与之前相同，我们计算输入x与第一权重矩阵W1之间的点积，并将激活函数应用于所得向量以获得第一隐藏向量h1。现在将h1视为即将到来的第三层的输入。重复从之前开始的整个过程，直到获得最终输出y为止：

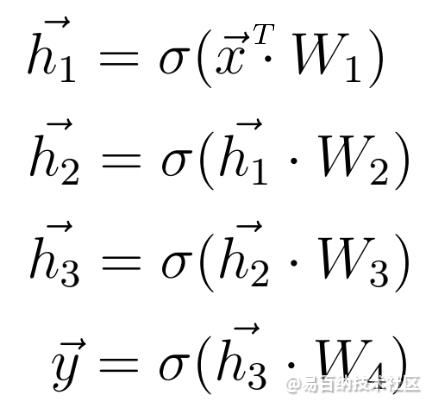
正向传播方程

在获得神经网络的预测之后，在第二步中，我们必须将此预测向量与实际的地面真相标签进行比较。我们将地面真相标签称为向量y_hat。

虽然向量y包含神经网络在正向传播过程中计算出的预测（实际上可能与实际值有很大不同），但向量y_hat却包含实际值。

8.损失函数

在数学上，我们可以通过定义一个损耗函数来测量y和y_hat之间的差，该函数取决于该差。一般损失函数的一个例子是二次损失：

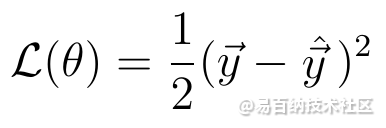
二次损失

此损失函数的值取决于y_hat和y之间的差。差异越大表示损耗值越高，差异越小表示损耗值越小。

最小化损失函数可直接导致神经网络的更准确预测，因为预测和标记之间的差异会减小。

最小化损失函数会自动使神经网络模型做出更好的预测，而不管当前任务的确切特征如何。您只需为任务选择正确的损失函数。幸运的是，您应该只知道两个损失函数，即可解决您在实践中遇到的几乎所有问题。

这些损失函数是交叉熵损失：

交叉熵损失函数

和均方误差损失：

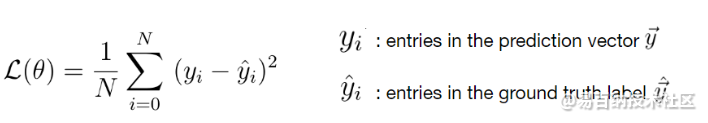
均方误差损失函数

由于损失取决于权重，因此我们必须找到一组特定的权重，其损失函数的值应尽可能小。通过称为梯度下降的方法在数学上实现了使损失函数最小的方法。

梯度下降

在梯度下降过程中，我们使用损失函数（或损失函数的导数）的梯度来改善神经网络的权重。为了理解梯度下降过程的基本概念，让我们考虑一个神经网络的非常基本的示例，该神经网络仅由一个输入神经元和一个输出神经元组成，并通过权重值w连接。

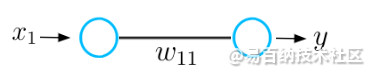
简单神经网络

该神经网络接收输入x并输出预测y。假设该神经网络的初始权重值为5，输入x为2。因此，该网络的预测y的值为10，而标签y_hat的值可能为6。

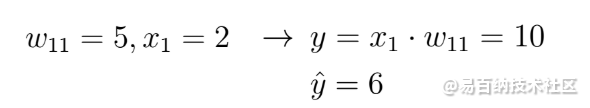
参数和预测

这意味着预测是不准确的，我们必须使用梯度下降法找到一个新的权重值，该值会导致神经网络做出正确的预测。第一步，我们必须为任务选择损失函数。让我们以我之前定义的二次损失为例，并绘制此函数，该函数基本上只是二次函数：

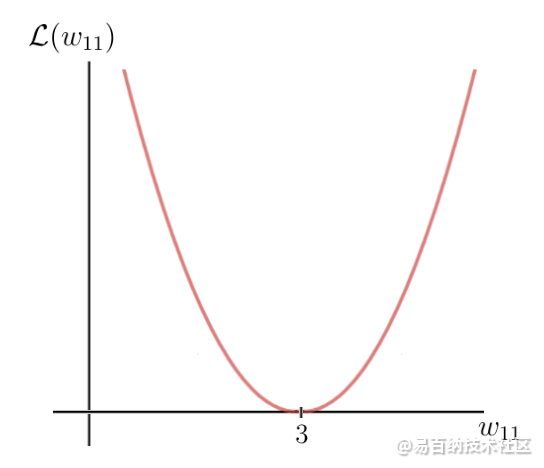
二次损失函数

y轴是损耗值，它取决于标签和预测之间的差异，并因此取决于网络参数（在这种情况下为一个权重w）。x轴表示此权重的值。如您所见，存在一定的权重w，损失函数达到全局最小值。该值是最优权重参数，它将导致神经网络做出正确的预测，即6。在这种情况下，最优权重的值将为3：

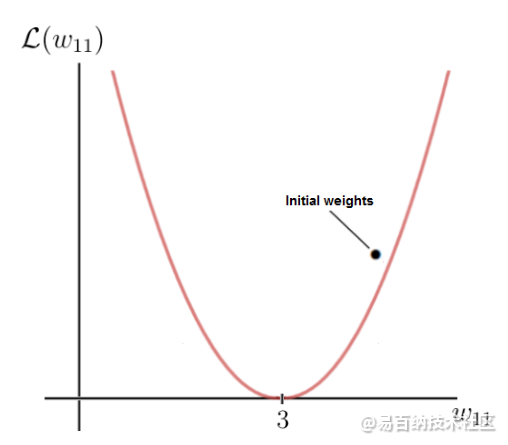
初始重量值

另一方面，我们的初始重量为5，这会导致相当高的损失。现在的目标是重复更新权重参数，直到达到该特定权重的最 佳值为止。这是我们需要使用损失函数的梯度的时候。幸运的是，在这种情况下，损失函数是单个变量的函数，即权重w：

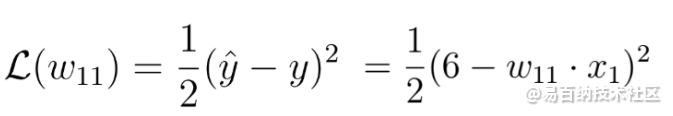
损失函数

针对该参数计算损失函数的导数：

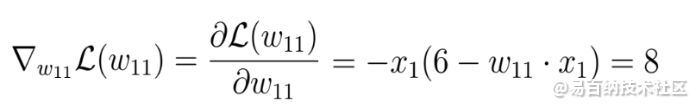
损失函数的梯度

这里得到的结果为8，它为我们的初始权重所在的x轴上的相应点提供了斜率或损失函数的切线值。该切线指向x轴上损失函数和相应的权重参数的最高增长率。

这意味着仅使用损失函数的梯度来找出哪些权重参数将导致更高的损失值。但是，我们想知道的恰恰相反。如果我们将梯度乘以负1并以这种方式获得梯度的相反方向，就可以得到想要的结果。通过这种方式，我们获得了损失函数最大降低率的方向以及导致这种降低的x轴上的相应参数：

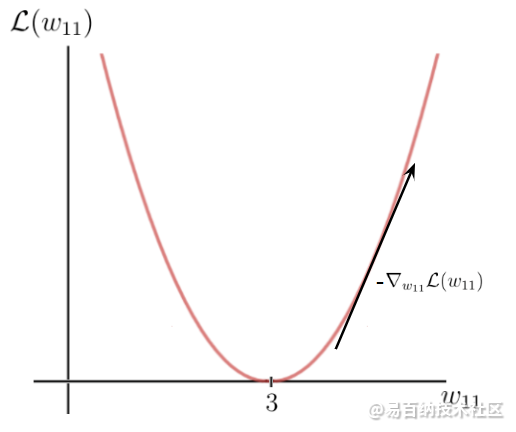
接下来，将执行一个梯度下降步骤，以尝试改善体重。我们使用此负梯度来沿权重的方向更新当前权重，对于这些权重，损失函数的值会根据负梯度减小：

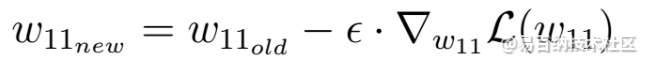
梯度下降步骤

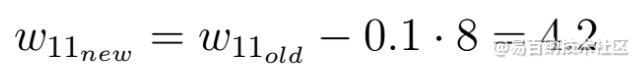
梯度下降步骤

这个方程中的ε因子是一个称为学习率的超参数。学习速率决定您要更新参数的速度或速率。请记住，学习率是我们必须乘以负梯度的参数，学习率通常很小。以上的学习率为0.1。

如您所见，梯度下降之后的权重w现在为4.2，并且相比梯度步骤之前的权重更接近最 佳权重。

梯度下降后的新权重

新权重值的损失函数的值也较小，这意味着神经网络现在能够进行更好的预测。您可以在脑海中进行计算，然后发现新的预测实际上比以前更接近。

每次执行权重更新时，我们都将负梯度向下移至最 佳权重。

在每个梯度下降步骤或权重更新之后，网络的当前权重将越来越接近最 佳权重，直到模型最终达到最 佳权重，并且神经网络将能够进行我们想要做出的预测。如此就完成了 整个模型学习的过程。