Python人工智能：基于sklearn的特征选择方法的详细总结

一、特征选择概述与数据集的获取

1. 特征选择概述

特征选择是将原始数据转换为能够更好地表征模型属性特征的过程。sklearn具有的数据预处理库Preprocessing库与降维方法库Dimensionality reduction，能够很好的实现特征选择相关工作。在特征选择过程中通常会遇到特征之间具有相关性、特征与标签无关、特征太多/太少等问题。对此，特征选择的目的通过解决这几个方面的问题，以达到降低计算成本与提高模型预测性能的目的。

通常，特征提取方法包括：(1)过滤法、(2)嵌入法、(3)包装法与(4)降维法四种，其中降维算法是最为常用的特征构造方法。下面分别使用sklearn来实现这四种方法。

2. 数据集获取与其结构信息查看方法

本文使用的数据集为手写数字的识别数据集，可以通过百度网盘链接下载：

链接: https://pan.baidu.com/s/138UokPNIOTdl8bTLUBQKxA?pwd=wktm，提取码: wktm。

手写数据集是机器学习非常常用的数据集，其中数据特征包含0-9的手写数字像素（共28×28=784），同时还包含0-9的10个标签。将下载好的数据集放入到当前Python编程环境的目录下，手写数据集信息的查看方法可以通过如下命令查看：

import pandas as pd

# 读取手写数据
data = pd.read_csv("./digit_recognizor_dataset/train.csv")
# 设置显示的最大列数为8
pd.set_option("display.max_columns", 8)

data.head()

手写数据集的整体结构如下图所示：

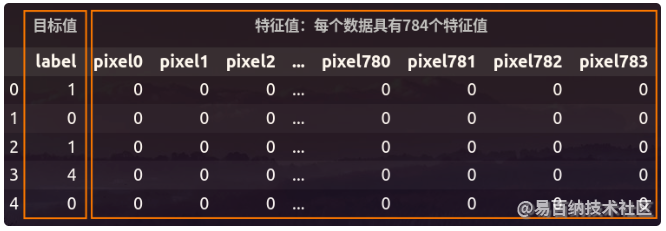
通过下面的指令可以查看数据的形状及缺失值：

# 查看数据集形状
print("\n数据集共有{}个数据点，{}列数据\n".format(
    data.shape[0], data.shape[1]
))

# 查看数据中是否具有缺失值
print("数据集中是否有缺失值:{}".format(data.isnull().sum().any()))

由于数据集具有784个特征，如果直接使用机器学习算法进行计算则会非常耗费时间，因此，在进行计算之间通常需要进行特征选择操作。

另外，由上图可以看出数据集中没有缺失值，因此，我们就可以直接使用数据集进行特征选择。下面将特征与标签分离，就可以开始本文的讲解了。

# 下面将特征与标签分离
X = data.iloc[:, 1:]
y = data.iloc[:, 0]

二、主成分分析法特征选择

1. 主成分分析法简介

对于高维数据，通常会存在一些特征不带有效信息（比如噪声）或特征之间具有重复信息的特征（比如一些特征之间线性相关性很大）。因此，我们希望寻找一种方法可以衡量特征上所带的信息，合并带有重复信息的特征，并删除带有无效信息的特征，以实现既能减少特征的数量，又能保留大部分有效信息。

主成份分析法（PCA, Primary Component Analysis），该方法使用样本的方差（也叫作可解释性方差）作为特征信息衡量指标，其中某个方差越大则特征所包含的信息量越多。

sklearn中通过sklearn.decomposition.PCA类函数实现，其主要参数如下所示：

• (1) n_components：降维后的维度，即降维后需要保留的特征数，是一个介于0~数据集维度之间的一个整数[0, min(X.shape)]。
• (2) svd_solver=='full'：表示希望降维后的总解释性方差占比大于n_components指定的百分比，即希望保留百分之多少的信息量，比如希望保留的信息量，则可以设置n_components=0.97，此时PCA会自动筛选出能够保留信息超过的特征数量。

2. 主成分分析法实现方法

• (1) 指定维度的参数使用方法

下面的代码将原始数据的维度降低为3维：

import pandas as pd
from sklearn.decomposition import PCA

# 读取手写数据
data = pd.read_csv("./digit_recognizor_dataset/train.csv")
# 下面将特征与标签分离
X = data.iloc[:, 1:]
y = data.iloc[:, 0]

# 构造主成份分析法实例，降维后的特征具有两维，便于特征绘图
pca = PCA(n_components=3)

# 降维后的数据为X_pca
X_pca = pca.fit_transform(X)

# 原始数据的维度信息
print("原始数据的维度:", X.shape)
print("降维后数据的维度:", X_pca.shape)

代码输出结果为：

• (2) 指定总解释性方差占比的参数使用方法

下面的代码希望降维后特征的总解释性方差占比大于97%的信息，另外我们可以使用sklearn.decomposition.PCA类方法的属性参数explained_variance_ratio_来查看降维之后特征的总解释性方差占：

# 指定降维后总的可解释性占比的主成份分析法的实例化
pca_evr = PCA(n_components=0.97, svd_solver="full")

# 对原始数据集进行降维
pca_evr = pca_evr.fit(X)
# 获得降维后的数据集
X_pca = pca_evr.transform(X)

print("降维后的数据维度:", X_pca.shape)
print(
    "降维后数据的特征的可解释性方法占比:",
    pca_evr.explained_variance_ratio_.sum()
)

代码执行结果如下图所示：

三、Filter过滤法特征选择

过滤方法作为一种特征选择方法，通常用于机器学习的数据预处理阶段。它是根据各种统计检验中的分数以及相关性的指标来进行特征选择的，据此，过滤法可以分为：方差过滤法与相关性过滤法两种。

1. 方差过滤法

方差过滤法是一种通过特征本身的方差来筛选数据特征的方法。方差过滤的整体思路为：数据集中的某个特征的方差很小，则认为该特征对于模型的表征贡献不大。

• (1) sklearn中的方差过滤函数VarianceThreshold

通过sklearn的VarianceThreshold函数我们可以很容易地实现方差过滤法特征选择。

其中VarianceThreshold具有非常重要的参数方差的阈值threshold，其功能是舍弃所有方差小于threshold的特征。默认情况下，该参数为，即删除所有具有相同值的特征。其代码如下所示：

from sklearn.feature_selection import VarianceThreshold

# 实例化方差过滤法特征选择实例，使用默认参数删除方差为零的特征
Var_feature_select = VarianceThreshold()
# 进行方差过滤后的特征数据
X_var = Var_feature_select.fit_transform(X)

# 首先查看使用方差过滤法之前与之后特征的数量
print(
    "\n方差过滤之前数据的特征数量为:{} \
    \n\n方差过滤之后数据的特征数量为:{}".format(
        X.shape[1], X_var.shape[1]
    )
)

由此可以看出经过方差过滤方法进行特征选择后，过滤掉了76个特征值。

但是，经过过滤掉数据中方差为0的特征后，数据的特征还是很多，我们还需要进一步进行特征过滤。此时我们就需要使用VarianceThreshold函数的方差的阈值threshold参数加大过滤的力度。

比如，如果我们选择原始特征数据X的中位数np.median(X.var().values)作为threshold参数的取值，则可以过滤掉更多的特征，代码如下所示：

import numpy as np

# 实例化能够过滤掉小于特征数据中位数的实例方法
# 并对原始特征数据X进行方差特征过滤
X_var_median = VarianceThreshold(
    np.median(X.var().values)
).fit_transform(X)

# 首先查看使用方差过滤法之前与之后特征的数量
print(
    "\n方差过滤之前数据的特征数量为:{} \
    \n\n方差过滤之后数据的特征数量为:{}".format(
        X.shape[1], X_var_median.shape[1]
    )
)

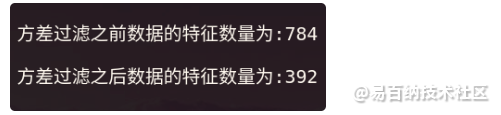
如上图所示，使用原始数据中位数作为方差过滤法的阈值参数后，特征数量会减少为原来的一半。

• (2) 超参数threshold的选择

通常情况下，VarianceThreshold函数的方差阈值超参数threshold过小过大都不能取得理想的特征选择效果。虽然我们可以使用学习曲线的方法确定合理的threshold值，但是对于数据量稍微大一点的数据集其运算时间通常很长。所以，在实际应用中，超参数threshold的选择通常使用默认值，对数据进行初步过滤即可，也就是说方差过滤法通常被用来辅助特征选择的工作。

2. 相关性过滤法

过滤掉方差为的特征后，我们通常需要进一步研究每个特征与标签之间的相关性，通过相关性研究我们可以剔除跟标签相关性比较差的参数，这样不仅不会过多的减少模型的预测精度，更重要的是可以极大的减少计算时间。

sklearn提供了三种常用的特征与标签之间相关性分析方法：(1)卡方过滤方法，(2)F检验方法，(3)互信息方法。

• (1) 卡方过滤：离散标签过滤方法

卡方过滤是专门针对离散标签的相关性过滤，即分类问题的相关性特征过滤方法。通过计算每个非负值特征与标签之间的卡方统计量，并按照统计量由高到底为特征进行重要性排序，以实现特征过滤的目的。

在sklearn中可以很方便地通过feature_selection.SelectKBest方法结合feature_selection.chi2卡方方法实例对象来实现卡方特征过滤方法。

feature_selection.SelectKBest方法具有两个重要输入参数：(1)卡方方法实例对象feature_selection.chi2，(2)前K个分数最高的特征。

代码如下所示：

from sklearn.feature_selection import chi2
from sklearn.feature_selection import SelectKBest

# 选取卡方评分最高的前300个特征，即特征与标签相关性最高的
# 前300个特征
X_chi2 = SelectKBest(
    chi2,   # 卡方评分方法实例对象
    k=300,  # 特征与标签相关性最高的前300个特征
).fit_transform(
    X_var,   # 以方差过滤后的数据为处理对象
    y        # 标签
)

print("经过卡方过滤后的数据形状{}".format(X_chi2.shape))

输出如下图所示：

• SelectKBest方法中的前K个分数最高的特征参数k对于特征选取性能具有重要影响。通常情况下，我们可以使用学习曲线方法来获取最 佳的k值。

学习曲线虽然可以很直观地表现出参数k对特征选取性能的影响，但是这种方法如果遇到数据量与特征值特别大的时候，计算时间会非常长。对此，我们可以选择另外一种更好的k值确定方法：基于显著性水平p值的k值确定法。

从特征选取角度，我们希望选取卡方值很大，同时p值小于0.5的特征，即特征与标签具有相关性。使用sklearn实现和中选择过程为：在调用SelectKBest函数之前，我们可以直接从chi2实例化后的模型中获得各个特征对应的卡方值与P值，从而根据上面的表格确定最优的k值，代码如下所示：

# 通过chi2方法获取各个特征数据与标签的卡方值chi_val与p值p_val
chi_val, p_val = chi2(X_var, y)

# 根据每个特征的卡方值与p值确定最 佳的k值
k = chi_val.shape[0] - (p_val > 0.05).sum()

• (2) F检验——可以针对回归与分类方法进行线性关系分析

F检验（又称为ANOVA，方差齐性检验）是用来获取每个特征与标签之间的线性关系的过滤方法，它即可以用于回归分析也可以做分类分析。sklearn中提供了两个F检验函数：feature_selection.f_classif用于分类问题的F检验，即标签是离散变量的数据；feature_selection.f_regression用于回归问题的F检验，即标签是连续变量的数据。

其用法与卡方检验相似，需要与SelectKBest结合使用，并且我们可以很方便的通过F检验输出结果确定SelectKBest的参数k。需要注意的是：F检验针对正态分布数据具有很好的稳定性，因此，在使用F检验进行特征过滤之前，可以将数据转为为正态分布。

F检验会返回F值与p值两个统计量，与卡方过滤相似，p<=0.05的特征与标签具有显著线性相关性；而对于p<=0.05的特征则与标签不具有显著线性相关性，通常我们可以将他们剔除。

首先使用F检验确定SelectKBest的参数k的最 佳取值，然后结合SelectKBest进行F检验特征过滤，代码如下所示：

from sklearn.feature_selection import f_classif

F, p_val_F = f_classif(X_var, y)

# 通过F检验确定SelectKBest方法最 佳K值
k = F.shape[0] - (p_val_F > 0.05).sum()

# 进行F检验特征过滤
X_F = SelectKBest(
    f_classif,     # F检验方法实例对象
    k=k,           # 最优的k值
).fit_transform(
    X_var,   # 以方差过滤后的数据为处理对象
    y        # 标签
)

X_F.shape

• (3) 互信息法

互信息法是用来获取特征与标签之间的任意关系（线性与非线性关系）的特征过滤方法。与F检验相似，它可以对回归问题与分类问题进行分析，sklearn中可以通过feature_selection.mutual_info_classif(互信息分类)与feature_selection.mutual_info_regression(互信息回归)两个函数来实现特征与标签的互信息分析。

与F检验不同，互信息法返回位于[0 1]区间内的估计值，该估计值表示一个特征与标签之间的互信息量的程度。其中，表示特征与标签之间相互独立，而表示特征与标签之间完全相关。互信息分类问题的特征过滤示例代码如下所示：

from sklearn.feature_selection import mutual_info_classif

# 在法检验过滤特征处理数据的基础上进行互信息特征过滤
# 下面获取每个特征与标签的互信息估计multual_info_val
mutual_info_val = mutual_info_classif(X_F, y)

# 通过互信息估计结果确定SelectKBest方法最 佳K值
k = mutual_info_val.shape[0] - sum(mutual_info_val <= 0)

# 进行互信息特征过滤
X_mutual_info = SelectKBest(
    mutual_info_classif,   # 互信息方法实例对象
    k=k,                   # 最优的k值
).fit_transform(
    X_F,   # 以F检验过滤后的数据为处理对象
    y      # 标签
)

X_mutual_info

注意：互信息法虽然功能比F检验的强大，但是其计算时间却远大于F检验法。

四、Embedded嵌入法特征选择

sklearn的嵌入法是一种让算法自行决定使用那种特征过滤方法，即特征选择与训练同时进行的方法，我们可以简单地将其理解为过滤法的进化版。相对于过滤法，嵌入法的结果能够更好的精确到模型的效果本文，对于模型预测性能的提升具有很好的效果，其原理如下图所示：

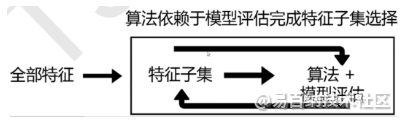
在sklearn中，我们可以很容易地通过feature_selection.SelectFromModel函数实现嵌入法特征选择。

SelectFromModel的模型选择机制为：比如具有feature_importance_的模型，由于feature_importance_的取值范围为[0 1]，其值越大特征的重要性越大，因此，SelectFromModel可以通过设置一个阈值threshold来剔除小于阈值的特征。

SelectFromModel具有很多输入参数，但是实际应用通常只需要关心如下两个参数即可：

• (1) estimator：模型评估器，只要带有feature_importances_、coef_属性，或带有l1或l2惩罚项的模型都可以使用；
• (2) threshold：模型重要性的阈值，重要性低于该阈值的特征将会被剔除。

下面以随机森林为例，使用SelectFromModel方法来实现嵌入法特征选择方法：

import pandas as pd
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier

# 读取手写数据
data = pd.read_csv("./digit_recognizor_dataset/train.csv")
# 下面将特征与标签分离
X = data.iloc[:, 1:]
y = data.iloc[:, 0]

# 构造随机森林模型实例
RFC = RandomForestClassifier(n_estimators=10)

# 使用SelectFromModel实现嵌入法特征选择
# 将特征重要性属性参数feature_importance_小于0.005的特征剔除
X_embedded = SelectFromModel(
    RFC, threshold=0.005
).fit_transform(X, y)

# 查看特征选择结果
print("\n原始数据具有{}个特征\n".format(X.shape[1]))
print("经过嵌入法特征选择后数据具有{}个特征".format(X_embedded.shape[1]))

执行结果如下图所示：

五、Wrapper包装法特征选择

包装法整体来说与嵌入法相似，其原理如下图所示，不同点主要体现在每次特征选择之后，下次特征选择的时，会在剔除特征的基础上进行算法的迭代。因此，我们可以将包装法视作筛选法与嵌入法的折中，在保证特征选择的合理性的情况下，尽可能地减少模型的计算时间。

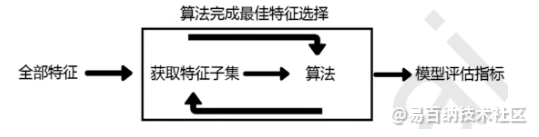
在sklearn中包装法是通过feature_selection.RFE类函数（RFE, Recursive Feature Elimination）实现的，其主要参数及其含义如下表所示：

另外,feature_selection.RFE还有两个重要属性：

• (1) .support_：返回所有的特征是否最后被选中的布尔矩阵；
• (2) .ranking_：返回特征的综合重要性排名。

包装法特征选择的实现代码如下所示：

from sklearn.model_selection import cross_val_score
import pandas as pd
from sklearn.feature_selection import RFE
from sklearn.ensemble import RandomForestClassifier

# 读取手写数据
data = pd.read_csv("./digit_recognizor_dataset/train.csv")
# 下面将特征与标签分离
X = data.iloc[:, 1:]
y = data.iloc[:, 0]

# 构造随机森林模型实例
RFC = RandomForestClassifier(n_estimators=10)

# 构造包装法特征选择方法对象
RFE_selector = RFE(
    RFC, n_features_to_select=340, step=50
).fit(X, y)

# 使用support_属性与ranking_属性查看包装法的特征选择情况：
print("共剔除了多少个特征:", RFE_selector.support_.sum())
print("选中的特征的重要性排名:", RFE_selector.ranking_)

# 经过包装法特征选择后的数据
X_wrapper = RFE_selector.transform(X)

# 使用交叉验证查看经过包装法特征选择后数据预测结果
print(
    "经过包装法特征提取后，模型的预测结果:",
    cross_val_score(RFC, X_wrapper, y, cv=5).mean()
)