Python人工智能：基于sklearn的K-means聚类算法的详细总结

一、K-means聚类算法简介

1. 聚类算法

聚类算法又称为无监督分类，其目的是根据数据的属性将数据划分为若干个类组（簇），通常用于但所数据的结果和分布等信息。比如，根据某些用户的消费信息，将用户划分为不同类型的消费群体。聚类算法的应用场景通常分如下内容：

• (1) 数据降维；
• (2) 矢量量化(Vector Quantization)；
• (3) 将高维数据压缩为列向量，常用于图像、声音、视频等非结构化数据，以达到数据压缩的目的。

2. K-means聚类算法工作原理

K-means聚类算法是最简单且最常用的聚类算法之一，为了更好理解K-means算法的工作原理，我们需要理解如下几个概念：

• (1) 簇：K-means算法将一组N个样本的特征X划分为K个无交集的簇，在一个簇中的数据就是同一类数据，簇的个数K是一个超参数，需要我们事先人为确定；
• (2) 质心：簇中所有数据的均值称为质心(centroids)。

K-means算法的核心任务：根据设定好的簇数K，寻找出最优的K个质心，并将距离质心最近的数据划分到对应簇中。

3. 欧几里德距离的含义

聚类算法追求簇内差异小而簇见差异大，通常情况下，我们使用样本点到其所在簇的质心距离之和来衡量，如果这个距离越小，则表示簇内样本相似度高。常用的距离表示方式包括：欧几里德距离、曼哈顿距离以及余弦距离，其中最为常用则是欧几里德距离，其表示簇中所有样本点到质心距离的平方和。

因此，欧几里德距离又成为簇内平方和（CSS, Cluster Sum of Square），也称为Inertia。相应的，将一个数据集中所有簇的簇内平方和相加，就得到整体平方和（TCSS, Total Cluster Sum of Square），也叫做total inertia。Total Inertia越小，表示每个簇内样本越相似，聚类的效果越好。因此，KMeans聚类算法追求的是求解能够让Inertia最小化的质心，同时在不断的迭代过程中Total inertia也会越来越小。

因此，我们可以理解为：K-means聚类算法就是寻找使得簇内平方和或整体平方和最小的每个簇的质心过程。

4. K-means算法的时间复杂度

除了模型本身效果之外，在实际应用中我们还需要考虑算法复杂度，算法复杂度通常分为：

• 时间复杂度：执行算法所需要的计算工作量，通常O用来表示；
• 空间复杂度：执行算法所需要的内存空间。

对于K-means算法的平均复杂度为O=（k×n×T），其中是k簇数，n是样本数，T为迭代次数。

二、K-means聚类算法的方法sklearn.clster.KMeans的简介

sklearn中可以通过sklearn.cluster.KMeans类函数来实现K-means聚类算法，本小节主要从以下三个方面来介绍KMeans类函数的使用方法：

• Kmeans函数的简单实例；
• KMeans函数的重要参数；
• Kmeans函数的重要属性与接口。

1. 基于KMeans函数聚类算法的简单示例

下面给出一个简单的K-means聚类算法实现方法：

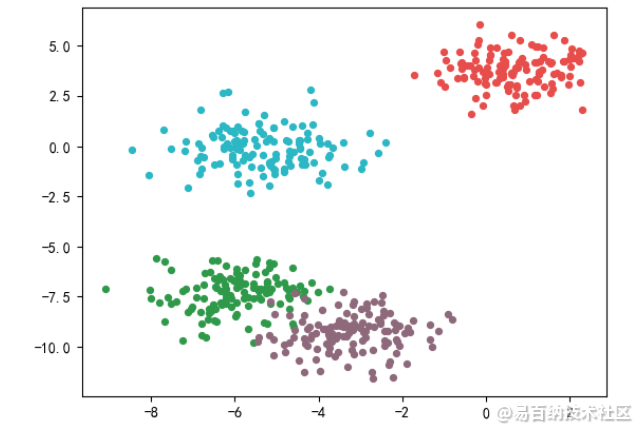
• 首先是数据集的构建与可视化

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 创建自己的数据集并绘制数据集
X, y = make_blobs(
    n_samples=500,  # 样本数
    n_features=2,   # 特征数
    centers=4       # 质心数
)

# 每个簇数据的颜色
color = ["#33984b", "#8d697a", "#e64e4b", "#2fb6c3"]
fig, ax1  = plt.subplots(1)

for i in range(4):
    ax1.scatter(
        X[y==i, 0], X[y==i, 1],
        marker='o', # 散点的数据形状
        s=18,       # 数据点的大小
        c=color[i]
    )
plt.show()

代码输出：

• 然后，使用sklearn.cluster.KMeans类方法进行聚类分类操作，并输出聚类结果、簇的质心以及总的簇内平方和：

# 下面进行K-means算法对数据进行聚类
from sklearn.cluster import KMeans

# 实例化K-means聚类算法，并对数据X进行聚类分类操作
cluster = KMeans(n_clusters=4).fit(X)

# 我们可以使用KMeans类方法的属性labels_查看聚类算法分类结果
print("聚类算法的预测分类结果:", cluster.labels_)

代码输出如下图所示：

我们还可以使用sklearn.cluster.KMeans类方法属性cluster_centers_来查看K-means聚类结果的质心：

print("聚类算法的预测质心:", cluster.cluster_centers_)

代码输出结果为：

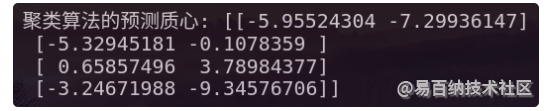
我们还可以使用sklearn.cluster.KMeans类方法属性inertia_来查看K-means聚类结果总的簇内平方和：

print("聚类算法的结果总的簇内平方和:", cluster.inertia_)

代码执行结果如下图所示：

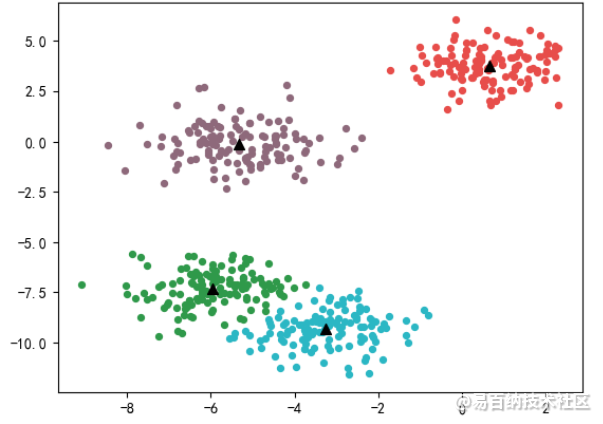
• 最后，绘制聚类结果图：

fig, ax2 = plt.subplots(1)

# 绘制预测聚类结果散点图
for i in range(4):
    ax2.scatter(
        X[cluster.labels_ == i, 0],
        X[cluster.labels_ == i, 1],
        marker='o',
        s=18,
        c=color[i]
    )

# 绘制簇的质心
ax2.scatter(
    cluster.cluster_centers_[:,0],
    cluster.cluster_centers_[:,1],
    marker="^",
    s=50,
    c="black"
)

plt.show()

代码执行结果如下图所示：

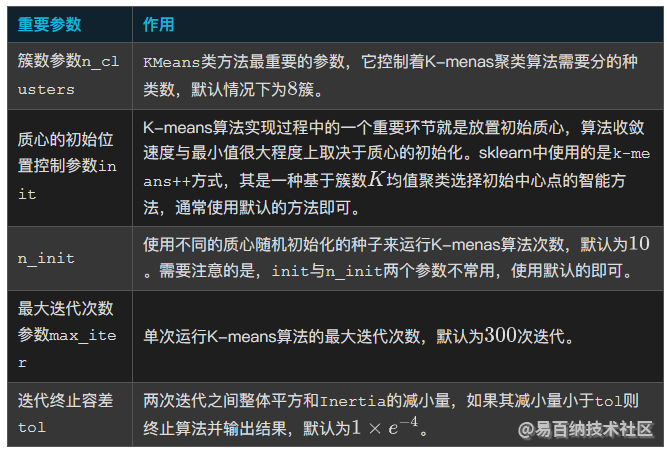
2. KMeans函数的重要参数

KMeans函数的重要参数及其作用如下表所示：

3. KMeans函数的重要属性与重要接口

KMeans函数的重要属性如下表所示：

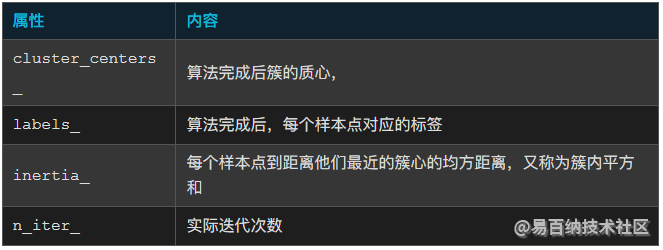
KMeans函数的重要接口如下表所示：

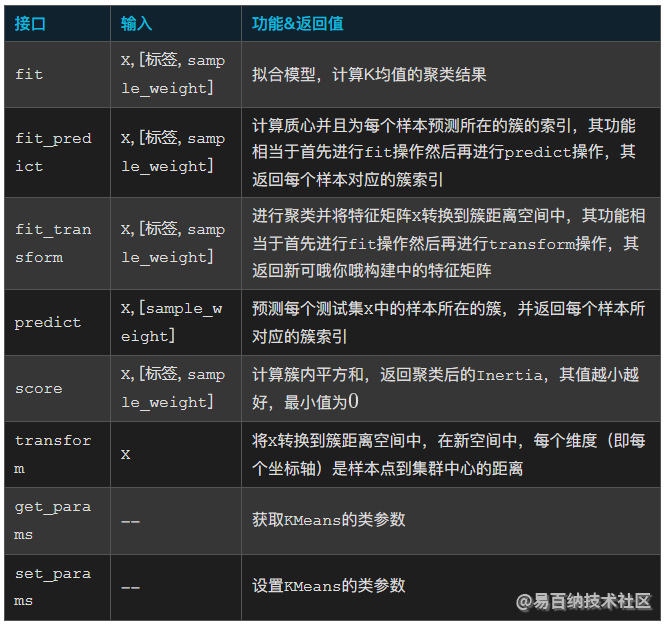
三、K-meas算法的评价指标及其实现示例

对于聚类算法通常分为标签已知与标签未知两种情况。由于实际情况下，聚类算法的标签通常是未知的，对于标签未知的聚类算法通常使用轮廓系数作为评价指标。

1. 当真实标签已知的评价指标

对于标签已知的数据集可以通过如下表所示的指标对聚类算法进行衡量：

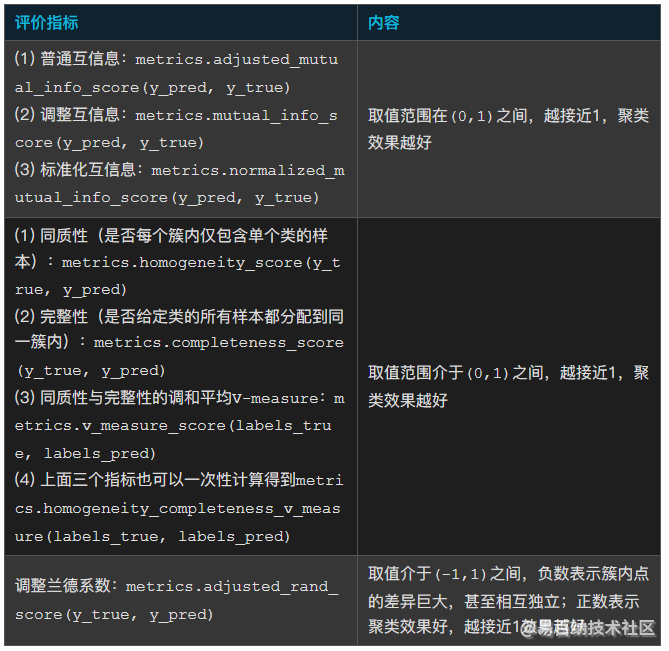
2. 当真实标签未知的评价指标：轮廓系数

对于聚类分析的数据通常情况下，我们是不知道它们的标签的。此时，我们只能通过评价簇内的稠密程度（簇内差异小）与簇间的差异程度（簇外差异大）来评估聚类的效果。其中聚类算法最常用的评价指标就是：轮廓系数，其定义如下所示：

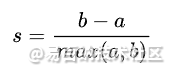
其中：

• a：样本与其自身所在簇中的其他样本的相似度，可用样本与同一簇中所有其他点之间的平均距离表示；
• b：样本与其他簇中样本的相似度，可用样本与下一个最近的簇中所有点之间的平均距离表示。

轮廓系数的取值范围介于(-1,1)之间，其中值越接近1表示样本与自己所在簇中的样本很相似，并且与其他簇中的样本不相似；而当样本点与簇外样本更相似的时，则轮廓系数为负值；当轮廓系数为0时，则表示两个簇中的样本相似度一致，两个簇可以划归为一个簇。

在sklearn中，我们可以通过如下两个方法计算轮廓系数：

• (1) metrics.silhouette_score(X, y_pred)：用来计算轮廓系数，它返回的是一个数据集中所有样本的轮廓系数的均值。
• (2) metrics.silhouette_samples(X, y_pred)：用来计算轮廓系数，但是其返回的是数据集中每个样本自身的轮廓系数。

3. K-means聚类算法 轮廓系数的可视化实例

代码如下所示：

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import pandas as pd
from sklearn.datasets import make_blobs

# 构建训练数据集
# 创建自己的数据集并绘制数据集
X, y = make_blobs(
    n_samples=500,  # 样本数
    n_features=2,   # 特征数
    centers=4       # 质心数为6
)

# 首先定义K-means聚类算法的超参素
n_clusters = 4

# 创建一个包含两个图片的画布
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(11, 4.5)  # 绘制画布

# (1) 第一个图ax1用于绘制轮廓系数：其是由各簇的轮廓系数构成的线条图
# x周为轮廓系数，y周为每个样本。

# 由于轮廓系数的取值范围在[-1,1]之间，为了使得绘图效果更加美观，
# 这里设置x轴的取值范围介于[-0.1,1]之间
ax1.set_xlim([-0.1, 1])

# 接下来绘制ax1的纵坐标
ax1.set_ylim([0, X.shape[0] + (n_clusters + 1) * 10])

# 开始模型的构建，调用聚类好的标签
cluster = KMeans(n_clusters=n_clusters).fit(X)  # 模型构建
cluster_labels = cluster.labels_                # 获取预测标签

# 使用轮廓系数计算函数silhouette_score得到所有样本轮廓系数的均值
silhouette_avg = silhouette_score(X, cluster_labels)

# 另外，为了得到图1的x轴坐标，我们需要使用silhouette_samples
# 得到每个样本点的轮廓系数
sample_silhouette_values = silhouette_samples(X, cluster_labels)

# 设定y轴上的初始值
y_lower = 10

# 对每个簇进行循环
for i in range(n_clusters):
    # 从每个样本的轮廓系数结果中提取第i个簇的轮廓系数，并对其进行排序
    ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
    # 注意：.sort()直接改掉原始数据的顺序
    ith_cluster_silhouette_values.sort()
    # 查看每个簇中分别具有多少个样本
    size_cluster_i = ith_cluster_silhouette_values.shape[0]
    # 每个簇在y轴上的取值，其起始位置为y_lower，终止位置为y_lower+簇中样本的结束位置y_upper
    y_upper = y_lower + size_cluster_i

    # 下面使用colormap库为每个簇分配不同的颜色，具体是使用小数来调用颜色的函数
    # 即在nipy_spectral([输入任意小数来代表一个颜色])
    color = cm.nipy_spectral(float(i) / n_clusters)

    # 下面填充ax1的内容，用到的方法如下所示：
    # fill_between(坐标下限,坐标上限,柱状图颜色)：让一个范围内的柱状图都同意颜色
    # fill_betweenx(坐标下限,坐标上限,柱状图颜色)：作用在x轴上
    # fill_betweeny(坐标下限,坐标上限,柱状图颜色)：作用在y轴上
    ax1.fill_betweenx(
        np.arange(y_lower, y_upper),
        ith_cluster_silhouette_values,
        facecolor=color,
        alpha=.7
    )

    # 使用text(要显示编号位置的x坐标,要显示编号位置的y坐标,要显示编号的内容)，
    # 函数为每个簇的轮廓系数添加簇的编号，并让簇的编号显示坐标轴上每个条形图的
    # 中间位置
    ax1.text(
        -.05,
        y_lower + .5 * size_cluster_i,
        str(i)
    )

    # 每次迭代完成，将y轴的起始位置对当前嘴上的位置再向上移动10个距离
    y_lower = y_upper + 10

# 绘制样本的K-means聚类后的轮廓曲线图
ax1.set_title("不同簇的轮廓曲线")
ax1.set_xlabel("样本的轮廓系数值")
ax1.set_ylabel("聚类标签")

# 进而将整个数据集上的轮廓系数的均值以虚线的形式添加到图中
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")

# 去掉y轴的刻度
ax1.set_yticks([])
# 重新绘制x轴刻度
ax1.set_xticks([-.1, 0, .2, .4, .6, .8, 1])

# (2) 第二个图的绘制，首先获取心的颜色
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)

# 绘制数据集的散点图
ax2.scatter(
    X[:, 0], X[:, 1],
    marker='o',
    s=18,
    c=colors
)

# 绘制K-means聚类算法后的质心
centers = cluster.cluster_centers_
ax2.scatter(
    centers[:, 0], centers[:, 1],
    marker='^', c='red',
    alpha=1, s=80
)

# 绘制标题，坐标标签
ax2.set_title("聚类数据的可视化")
ax2.set_xlabel("第一个特征的特征空间")
ax2.set_ylabel("第二个特征的特征空间")

# 为整个图设置标题
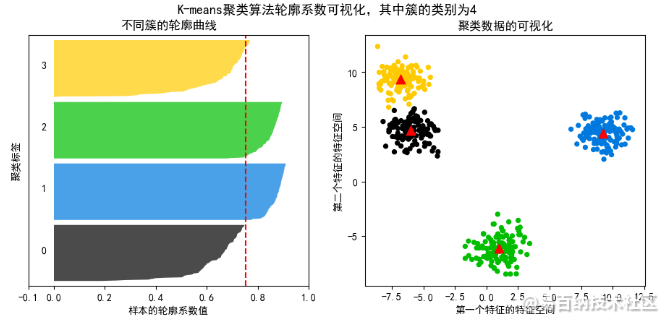
plt.suptitle(
    ("K-means聚类算法 轮廓系数可视化，其中簇的类别为%d" % n_clusters),
    fontsize=13, fontweight='bold'
)

代码执行结果为：