GBDT梯度提升树(回归)算法的理解与简单实现

Boosting tree(提升树)中，当损失函数是平方损失或指数损失时，每一步优化都很简单，对于平方损失，最优的决策树只需要拟合残差即可，对于指数损失，则等价于Adaboost。但是当损失函数是更一般的函数时，如何对损失函数优化来求出下一棵最优的决策树呢？针对这个问题Freidman提出了Gradient Boosting(梯度提升,GBDT)算法。本文以及下一篇文章对此进行介绍。

算法推导

对于加法模型：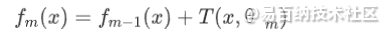

第m轮时，我们需要最小化可微的损失函数：

对损失函数在处做泰勒一阶展开:

这里待求解的是第m棵决策树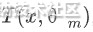，我们的目标是增加的第m棵决策树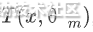后能使损失函数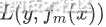减小，而且减小的尽可能的多。由于负梯度是一个函数局部下降最快的方向，因此优化时第m棵决策树应该朝负梯度方向进行调整，调整多少呢？一般调整负梯度值的η倍：

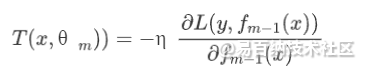
η称为学习率，应该是一个较小的数，这使得足够小，这样泰勒一阶展开才会有效。从公式来看，第m棵决策树只需要拟合损失函数η倍的负梯度在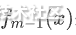处的值就可以了。如果熟悉最优化理论，容易发现GBDT本质上就是在采用梯度下降法去求解损失函数的最优解。更具体一点，GBDT就是用一颗颗决策树去拟合负梯度。

有了上述优化算法，我们就能得到一棵棵决策树，进而相加得到最终的模型。所以我们看到GBDT的核心就在计算损失函数的负梯度上面。我们知道，机器学习的损失函数一般分为分类和回归两类，下面我们着重介绍回归问题几种常用的损失函数及其负梯度的计算，关于分类任务常用的损失函数及其负梯度的计算我们留到下一篇文章再来介绍。

平方损失

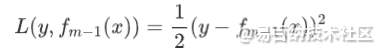
其负梯度为：

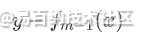
可以看到，当损失函数为平方损失时，梯度就等于残差，那么下一棵决策树拟合的就是残差，这正好对应了上一篇文章我们介绍的boosting tree(提升树)，因此我们说boosting tree其实可以看作是Gradient Boosting的一个特例。

绝对损失

其负梯度为：

huber损失

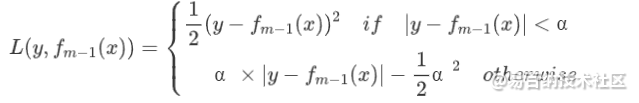
其负梯度为

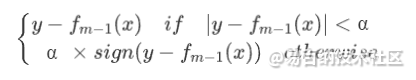
分位数损失

注意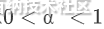，其负梯度为

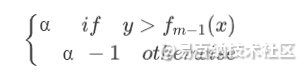
这些损失函数各有各自的使用场景，如果要深究能写很多东西，限于篇幅，我们这里仅仅简单提一下各个函数的优缺点：

• 平方损失的优点是容易求解，可以发现其梯度随着损失的减小而减小，这使得算法在迭代过程中更能得到精确的结果，但是缺点也比较明显，因为平方后对异常值很敏感，不够稳健；
• 绝对损失的优点是对异常值不敏感，但是可以看到它的导数是不连续的，这不利于算法的迭代；
• huber损失刚好结合了平方损失和绝对损失的优点，容易看出来，当α趋向于0时它就退化成了绝对损失，而当α趋向于无穷时则退化为了平方损失，正因如此huber损失无论是处理异常值，还是算法迭代，都能处理的比较好，但是huber损失也有缺点，就是合适的参数α并不容易确定；
• 分位数损失在做分位数回归时常用，它也是对绝对损失的推广，容易看出来当α=0.5时，分位数损失就退化为绝对损失，其优点也在于对异常值比较稳健。

GBDT回归算法的numpy实现

下面我们编写GBDT回归算法的numpy实现代码

import numpy as np
from sklearn.tree import DecisionTreeRegressor
class GBDTRegressor():
    def __init__(self,n_estimators,loss='ls',learning_rate=0.1,alpha=0.7,**kwargs):
        """
        Parameters
        ----------
        n_estimators：决策树数量
        loss：损失函数
        learning_rate：学习率
        alpha：huber损失和分位数损失的调节变量α
        kwargs：决策树参数
        """
        self.n_estimators = n_estimators
        self.loss = loss
        self.learning_rate = learning_rate
        self.alpha = alpha
        self.base_estimator = DecisionTreeRegressor(**kwargs)
        
    def __gradient(self,y,y_hat):
        """
        计算损失函数的梯度，ls为平方损失、lad为绝对损失、huber为huber损失、quantile为分位数损失。
        """
        if self.loss == 'ls':
            return y-y_hat
        elif self.loss == 'lad':
            return np.sign(y-y_hat)
        elif self.loss == 'huber':
            return np.where(np.abs(y-y_hat)<self.alpha,y-y_hat,self.alpha*np.sign(y-y_hat))
        elif self.loss == 'quantile':
            return np.where(y>y_hat,self.alpha,self.alpha-1)
        else:
            raise ValueError("The loss function can only be 'ls' or 'lad' or 'huber' or 'quantile'")
            
    def fit(self,x,y):
        self.estimators_ = []
        # 拟合第一棵决策树
        estimator_0 = self.base_estimator.fit(x,y)
        y_hat = estimator_0.predict(x)
        y_gradient = self.__gradient(y,y_hat)*self.learning_rate
        self.estimators_.append(estimator_0)
        # 用负梯度拟合剩下n-1棵决策树
        for i in range(self.n_estimators-1):
            params = self.base_estimator.get_params(deep=False)
            estimator = self.base_estimator.__class__(**params)
            estimator = estimator.fit(x,y_gradient)
            y_hat += estimator.predict(x)
            y_gradient = self.__gradient(y,y_hat)*self.learning_rate
            self.estimators_.append(estimator)
    
    def predict(self,x):
        return np.sum([estimator.predict(x) for estimator in self.estimators_],axis=0)

代码测试

下面的代码分别测试了损失函数分别为平方损失、绝对损失、huber损失和分位数损失的模型收敛情况。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split as tts
from sklearn.metrics import mean_squared_error as mse
import matplotlib.pyplot as plt
load = load_boston()
x = load.data
y = load.target
x_train,x_test,y_train,y_test=tts(x,y,test_size=0.3)

idx = []
mse_list = []
loss = ['ls','lad','huber','quantile']
fig = plt.figure(figsize=(18,12))
for i in range(len(loss)):
    for j in range(1,200):
        reg = GBDTRegressor(j,loss=loss[i],max_depth=1,alpha=0.8)
        reg.fit(x_train,y_train)
        pred = reg.predict(x_test)
        error= mse(y_test,pred)
        idx.append(j)
        mse_list.append(error)
    ax = fig.add_subplot(2,2,i+1)
    ax.plot(idx,mse_list)
    ax.set_xlabel('n_estimator')
    ax.set_ylabel('mse')
    ax.set_title(loss[i])
    idx=[]
    mse_list=[]

文章转载自公众号：用Python学机器学习