稀疏特征的 dropout 操作

稀疏特征的 dropout 操作 小菜很菜 2023-09-08 11:16:44 286
机器学习
深度学习
在深度神经网络中，当模型参数非常多并且训练数据量非常少的时候，在训练模型的过程中非常容易产生过拟合。其中，过拟合指的是模型在训练数据上面的表现非常的好，但是在测试数据上面的表现非常的差。因此，我们必然不会希望模型过拟合。防止过拟合的方法有很多种，比如增加训练数据量、减少模型的参数、权重参数的 L2 正则化，以及今天重点提及的 dropout 操作。

dropout 操作

dropout 操作是指在深度神经网络的训练过程中，每次训练都通过一个概率 p 来随机的让一些神经元的数值设置为 0（屏蔽部分神经元）。因为每次训练都很大概率屏蔽不同的神经元，进而导致网络结构发生变化，所以这样做的目的类似于训练多个网络求平均，可以有效防止过拟合。然而在测试过程中，我们对执行 dropout 操作的当前层保留所有的神经元并把输出权重乘上 1-p，这样做的目的是补偿训练期间被设置为 0 的神经元。换句话说，就是保证训练期间和测试期间相同样本的数学期望是一致的。下面我们来证明为什么上述做法可以保证训练期间和测试期间相同样本的数学期望是一致的。

证明：假设某一个样本在某一层的特征为向量 h。在训练过程中，进行 dropout 操作之后 h 的数学期望为 (1-p)h+p·0 = (1-p)h；在测试过程中，假设权重矩阵为 W，偏移向量为 b，那么进行 dropout 操作之后的 linear 变换公式为：(1-p)Wh+b，我们可以利用交换律和结合律重新整理一下进行 dropout 操作之后的 linear 变换公式：W[(1-p)h]+b，显然，我们可以发现在测试过程中，进行 dropout 操作之后的 h 的数学期望依旧是 (1-p)h。也就是说，上述做法可以保证训练期间和测试期间相同样本的数学期望是一致的。

虽然我在上文中解释了 dropout 操作的逻辑，但是目前的主流深度学习框架 PyTorch 中的 dropout 的实现逻辑和上文的逻辑略有不同，但是它们的实现逻辑和上文中的逻辑在数学上是完全等价的。

PyTorch 中的 dropout

我们来看一下在目前主流的深度学习框架 PyTorch 中的 dropout 是如何实现的。通过查阅 PyTorch 官方文档可知，我们可以发现在训练期间它不仅通过一个概率 p 来随机的让一些神经元的数值设置为 0，还把没有设置为 0 的神经元一律都乘上一个系数 1/(1-p)，测试期间直接完全忽略 dropout。这样的逻辑同样也可以保证训练期间和测试期间相同样本的数学期望是一致的。证明如下：

证明：假设某一个样本在某一层的特征为向量 h。在训练过程中，进行 dropout 操作之后的 h 的数学期望为 (1-p)[1/(1-p)]h+p·0 = h；在测试过程中，因为完全忽略了 dropout，所以进行 dropout 操作之后的 h 的数学期望和进行 dropout 操作之前的 h 的数学期望完全一致，都是 h。同样的，上述做法可以保证训练期间和测试期间相同样本的数学期望是一致的。

因此，不管是 PyTorch 中的 dropout 操作还是原始的 dropout 操作，它们都可以保证训练期间和测试期间相同样本的数学期望是一致的。

稀疏特征的 dropout 操作

虽然 dropout 通过类似于训练多个网络求平均来有效防止过拟合，但是当 dropout 操作用在某个稀疏特征（绝大多数特征取值为 0）上面，就会出问题了（不是程序报错，而是训练期间和测试期间的数学期望基本不可能一样了）。我们用原始的 dropout 逻辑进行证明。

证明：假设某一个样本在某一层的特征为向量 h。在训练过程中，我们假设 dropout 屏蔽掉的神经元原本取值已经是 0 了（这样的假设有很大概率发生，后续证明）。因此，进行 dropout 操作之后的 h 的数学期望依旧是 h；在测试过程中，显然，进行 dropout 操作之后的 h 的数学期望变成了 (1-p)h。也就是说，除非 dropout 的概率 p = 0，否则很大概率不可以保证训练期间和测试期间相同样本的数学期望是一致的。

事实上，PyTorch 中的 dropout 也存在这样的问题，依旧可以进行证明。

证明：假设某一个样本在某一层的特征为向量 h。在训练过程中，我们假设 dropout 屏蔽掉的神经元原本取值已经是 0 了。进行 dropout 操作之后的 h 的数学期望为 [1/(1-p)]h；在测试过程中，因为完全忽略了 dropout，所以进行 dropout 操作之后的 h 的数学期望和进行 dropout 操作之前的 h 的数学期望完全一致，都是 h。我们依旧得出了和上面一致的结论：除非 dropout 的概率 p = 0，否则很大概率不可以保证训练期间和测试期间相同样本的数学期望是一致的。

接下来我们证明为什么 dropout 屏蔽掉的神经元原本取值已经是 0 这一事件在稀疏特征中很大概率会发生。

证明：假设该稀疏向量的非零元素占比为 q（q 是一个很小的正数，非常接近 0）。因此，我们可以发现对非零元素进行 dropout 的概率是 pq。既然 q 都已经非常接近 0 了，概率 p∈[0,1]，所以一个非常接近 0 的数 q 乘上一个在 [0,1] 区间中的数 p，结果必然是接近 0。所以，在稀疏向量中去使用 dropout 操作会出现对非零元素进行 dropout 的概率非常的小，因此，在对稀疏向量用 dropout 的过程中 dropout 屏蔽掉的神经元原本取值已经是 0 的概率非常接近 1。

为了确保稀疏特征的 dropout 在训练期间和测试期间的数学期望一致，我们几乎不可能去使用针对非稀疏特征的 dropout，我们稍微改一下这个算子：针对稀疏特征，我们让 dropout 仅针对非零元素。这样的话就可以保证训练期间和测试期间相同样本的数学期望是一致的，首先基于原始的 dropout 操作给出证明。

证明：假设某一个样本在某一层的特征为稀疏向量 h。在训练过程中，因为 dropout 操作只考虑非零元素，所以显然进行 dropout 操作之后的 h 的数学期望为 (1-p)h+p·0 = (1-p)h（注意：因为 h 中的零元素乘上 1-p 还是 0，所以零元素不乘上 1-p 和乘上 1-p 是一回事，这就是为什么仅针对稀疏特征的非零元素进行 dropout 也是可行的，因为零元素不管用不用 dropout 结果都已经是 0 了）；在测试过程中，在测试过程中，假设权重矩阵为 W，偏移向量为 b，那么进行 dropout 操作之后的 linear 变换公式为：(1-p)Wh+b，我们可以利用交换律和结合律重新整理一下进行 dropout 操作之后的 linear 变换公式：W[(1-p)h]+b，显然，我们可以发现在测试过程中，进行 dropout 操作之后的 h 的数学期望依旧是 (1-p)h。所以，上述做法可以保证稀疏特征在训练期间和测试期间相同样本的数学期望是一致的。

同样的，我们也可以基于 PyTorch 中的 dropout 操作进行证明。

证明：假设某一个样本在某一层的特征为稀疏向量 h。在训练过程中，进行 dropout 操作之后的 h 的数学期望为 (1-p)[1/(1-p)]h = h，因为 0 乘上任何数结果都是 0，所以即使零元素不参与 dropout，给它乘上 (1-p)[1/(1-p)] 是完全没有问题的；在测试过程中，因为完全忽略了 dropout，所以进行 dropout 操作之后的 h 的数学期望和进行 dropout 操作之前的 h 的数学期望完全一致，都是 h。同样的，上述做法可以保证稀疏特征在训练期间和测试期间相同样本的数学期望是一致的。

给出了针对稀疏特征的合理的 dropout 算法，我们接下来就是基于主流深度学习框架 PyTorch 来实现这一算法。

sparse_coo_tensor

要想进行实现类似这样的针对稀疏特征的算法，我们首先必须知道 PyTorch 中有一个函数 sparse_coo_tensor，该函数用来创建稀疏张量，格式为 COO 格式。我们首先创建一个构造好数据集并把输入特征转化为 COO 格式的稀疏张量，在这里我选择 MNIST 手写数字数据集，我们把每一张 28✖28 的手写数字图像摊平，拉成一条 28*28 = 784 维的一个向量，数据集中的所有数据堆在一起构成了一个矩阵，代码如下：


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
print(X_train)

在这里我并没有通过 sparse_coo_tensor 函数来构造 COO 格式的稀疏张量，而是通过普通张量的 to_sparse 方法转换为 COO 格式的稀疏张量，最后我还加了一个输出，该输出的目的主要是查看 COO 格式的稀疏张量有哪些属性，输出结果如下图所示。

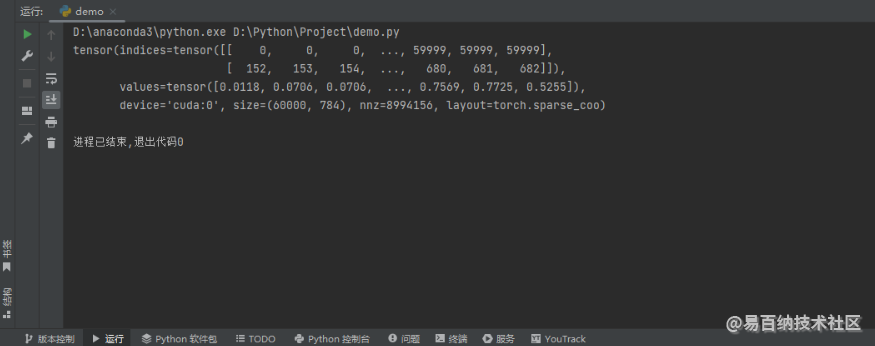
易百纳社区

我们可以发现它有着 indices 属性、values 属性、device 属性、size 属性，nnz 属性以及 layout 属性。我们尝试去访问这些属性，代码如下：


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
print(X_train.indices)
print(X_train.values)
print(X_train.device)
print(X_train.size)
print(X_train.layout)
print(X_train.nnz)

运行结果如下图所示。

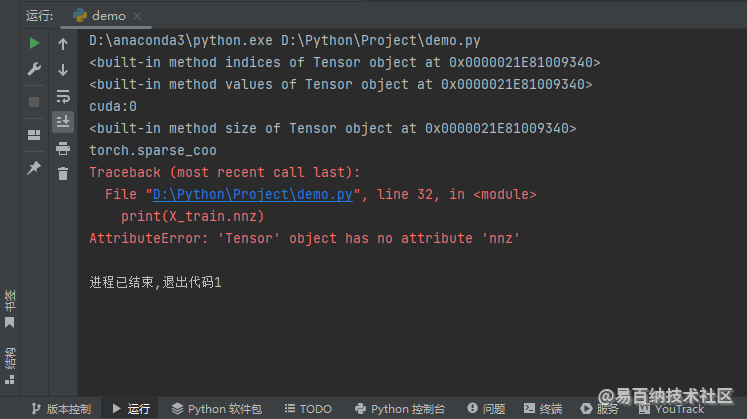
易百纳社区

device 属性表示它在什么设备上面，我这里的输出就是 GPU 了；layout 属性表示它的格式，在这里必然是 COO 格式的稀疏张量。同时，我们可以发现它并没有 nnz 属性，还有就是 indices、values 以及 size 并不是属性，而是方法，接下来我们看一下不给这 3 个方法提供参数是否可以拿到对应的 3 个属性，代码如下：

torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
print(X_train.indices())
print(X_train.values())
print(X_train.size())

运行结果如下图所示。

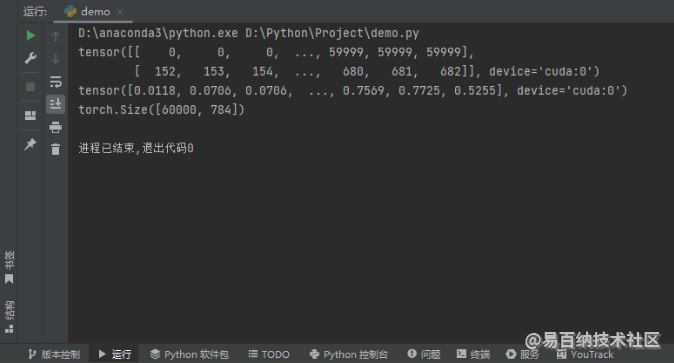
易百纳社区

显然，我们顺利拿到了 3 个属性。我们都知道，COO 格式只存储非零元素的索引和值，因此 indices 方法返回的是表示非零元素的索引的张量，values 方法返回的是表示非零元素值的一阶张量（一维数组）。我们把 indices 和 values 连在一起解读，就可以知道所有非零元素的所有信息了，我们把 values 堆叠到 indices 的下方（可以这么堆叠，不需要担心对不上，对不上的话后面的解释就不成立了），取出其中的任意一列构成一个三元组，比如我取第 0 列，这个时候三元组为 (0, 152, 0.0118)，它表示的意思是第 0 行第 152 列的元素是一个非零元素，其值为 0.0118。此外，需要注意的是这里的 size 方法我们完全可以改成 shape 属性。

考虑到稀疏特征 dropout 操作针对非零元素进行修改，非零元素对于 COO 格式的稀疏张量来说就是 values 方法的返回值。我们接下来就是需要知道 values 方法返回的是一个新数组还是返回一个指向 COO 格式的稀疏张量中的 values 属性的指针，代码如下：


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
values = X_train.values()
values[0] = -1
print(X_train)

在这里，我通过原地修改返回值，输出 X_train 来查看返回值是否已经被修改，运行结果如下图所示。

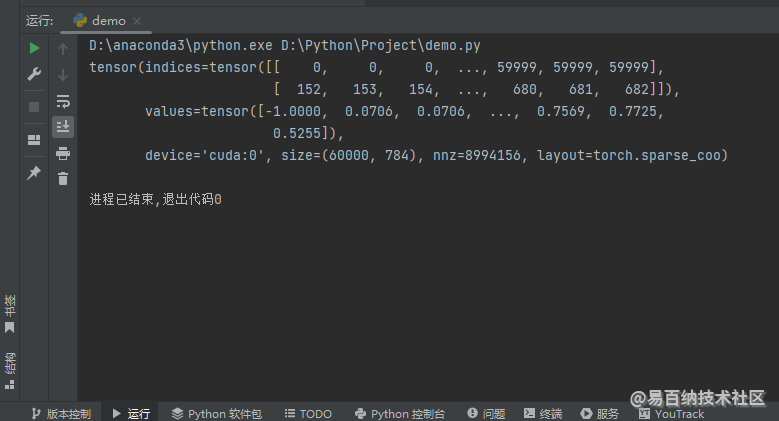
易百纳社区

我们可以发现 X_train 的 values 也跟着改掉了，这说明 values 方法的返回值是一个指向 values 属性的指针，不是一个新数组！这同时也说明了我可以通过修改 values 方法的返回值来修改 X_train 的 values 属性！关于 COO 格式的稀疏张量的介绍到此为止，我们接下来看一下稀疏特征的 dropout 操作如何来实现，分成了 2 节内容，一个是无梯度稀疏特征的 dropout 操作，一个是有梯度稀疏特征的 dropout 操作。

无梯度稀疏特征的 dropout 操作

我们首先看一下无梯度稀疏特征的 dropout 操作，首先构造一个含有无梯度特征的 dropout 操作的网络，代码如下：


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        x = self.dropout(x)
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

forward 方法中第一个 dropout 就是一个典型的无梯度特征的 dropout 操作，因为输入数据不会带有梯度。我们接下来尝试直接把之前的 X_train 和 X_test 传给 forward 方法 x 参数，看看能不能运行出来，代码如下：


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
values = X_train.values()
cross_entropy_loss_func, mlp = nn.CrossEntropyLoss().cuda(), MLP(X_train.shape[1], 10).cuda()
optimizer = Adam(mlp.parameters(), weight_decay=1e-4)
epochs = 200
for epoch in range(1, epochs+1):
    print(f'epoch = {epoch}')
    mlp.train()
    loss = cross_entropy_loss_func(mlp(X_train), y_train)
    optimizer.zero_grad(True)
    loss.backward()
    optimizer.step()
    mlp.eval()
    with torch.no_grad():
        print('Accuracy:', accuracy_score(y_test, mlp(X_test).argmax(1).cpu()))

运行结果如下图所示。

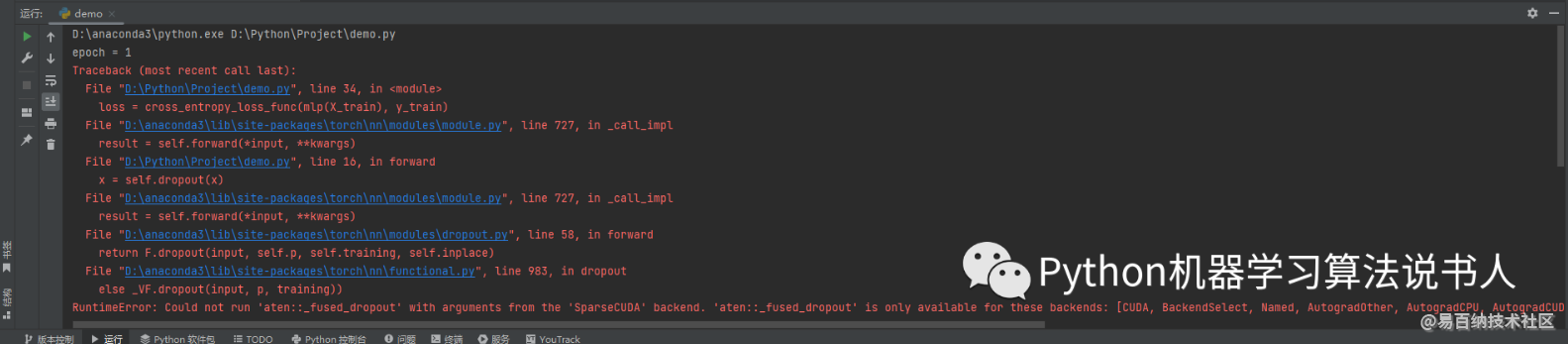
易百纳社区

从报错信息可以看出，dropout 操作不支持稀疏张量，我们完全不可能为了迎 合 dropout 操作而把稀疏张量转化为普通张量，因为这样走的就是非稀疏特征的 dropout 操作了。考虑到稀疏特征的 dropout 仅针对非零元素并且 COO 格式的非零元素可以通过 values 方法的返回值来获取，因此我们可以尝试对 values 方法的返回值 v 进行 dropout 操作，然后拿到 dropout 之后的 v，最后把它丢给 values 属性。代码如下：


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        values0 = x.values()
        values1 = self.dropout(values0)
        values0[:] = values1
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

我首先通过调用 values 方法来获取 values 属性，返回值记作 values0，然后对获取到的属性进行 dropout 操作（不是原地操作），返回值记作 values1，然后通过切片赋值来就地修改 values0，进而修改 values 属性。虽然看着逻辑没什么问题了，但是这样的写法存在这一个问题：因为 x 形参的类型是一个张量，而对于张量来说像这样传参传的是一个指针，对 x 形参的修改会反映到实参上面，也就是反映到输入数据上面，这会造成第 k+1 个 epoch 的数据用的是第 k 个 epoch 修改之后的数据，而不是原始数据。这绝对不可以！其实处理这个问题非常简单，我们不要去直接获取 x 的 values 属性，我们在此之前先把 x 复制一份，依旧用 x 来表示复制之后的 x，我们来修改复制之后的 x 的 values 属性就不会把修改反映到原始数据上面。我们只需要在 forward 方法体的第一行写上 x = x.clone() 就行了，代码如下：


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        x = x.clone()
        values0 = x.values()
        values1 = self.dropout(values0)
        values0[:] = values1
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

这样就没问题了，我们依旧用之前加载的数据集来训练这样的多层感知机，看看有没有什么问题，运行结果如下图所示。

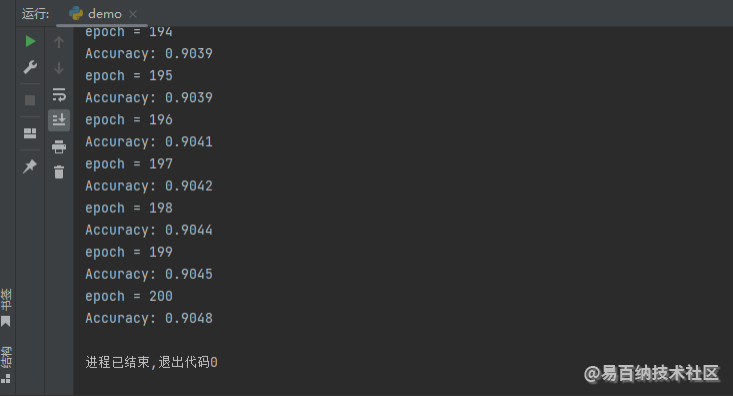
易百纳社区

最后，我们可以注意到：（1）当对 values0 进行 inplace 的 dropout 操作的时候，我们就不需要创建这个 values1 这个中间变量了。（2）因为 x 是输入数据的一个副本，所以对 x 的修改不会影响到输入数据。基于以上两点，我们可以把这个 dropout 操作改成 inplace 操作，代码如下：

class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.dropout_inplace = nn.Dropout(0.5, True)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        x = x.clone()
        values = x.values()
        self.dropout_inplace(values)
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

因为 dropout_inplace 走的是 inplace 操作（原地修改），所以不需要用返回值来接收修改后的值，更不需要做切片赋值了。同样用之前加载的数据集来训练这样的多层感知机，看看有没有什么问题，运行结果如下图所示。

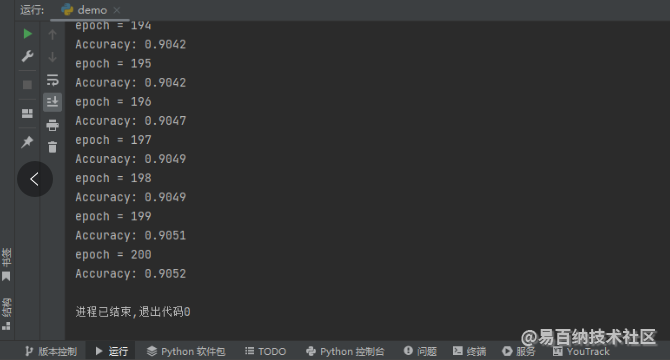
易百纳社区

至此，无梯度稀疏特征的 dropout 操作已经讲完了，接下来我们看一下有梯度稀疏特征的 dropout 操作。

有梯度稀疏特征的 dropout 操作

为了实现有梯度稀疏特征的 dropout 操作，我们先给稀疏张量 X_train 增加梯度，代码如下：


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = (X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255).requires_grad_()

这里我通过给稀疏张量调用 requires_grad_ 方法来增加梯度，其他地方我们什么都不动，代码如下：

from sklearn.metrics import accuracy_score
from torch import nn
from torch.optim import Adam
import torch


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.dropout_inplace = nn.Dropout(0.5, True)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        x = x.clone()
        values = x.values()
        self.dropout_inplace(values)
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))


torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
X_train, y_train = torch.load('MNIST/processed/training.pt', map_location='cuda')
X_test, y_test = torch.load('MNIST/processed/test.pt', map_location='cuda')
X_train = (X_train.reshape(X_train.shape[0], -1).to_sparse().float()/255).requires_grad_()
X_test, y_test = X_test.reshape(X_test.shape[0], -1).to_sparse().float()/255, y_test.cpu()
cross_entropy_loss_func, mlp = nn.CrossEntropyLoss().cuda(), MLP(X_train.shape[1], 10).cuda()
optimizer = Adam(mlp.parameters(), weight_decay=1e-4)
epochs = 200
for epoch in range(1, epochs+1):
    print(f'epoch = {epoch}')
    mlp.train()
    loss = cross_entropy_loss_func(mlp(X_train), y_train)
    optimizer.zero_grad(True)
    loss.backward()
    optimizer.step()
    mlp.eval()
    with torch.no_grad():
        print('Accuracy:', accuracy_score(y_test, mlp(X_test).argmax(1).cpu()))

我们运行上述程序，可以发现报错，报错截图如下所示。

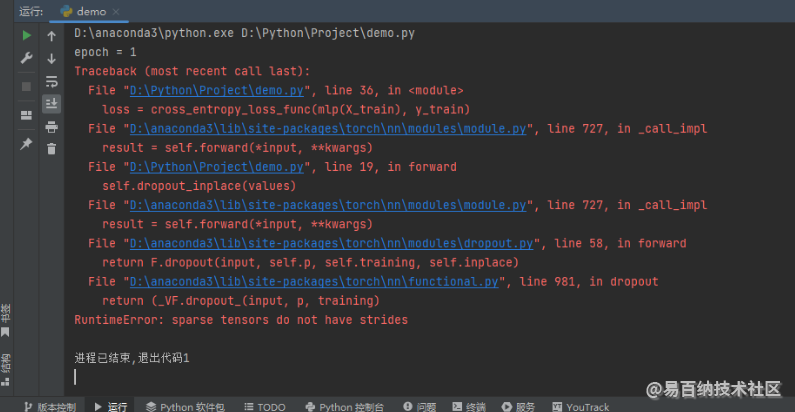
易百纳社区

这里的报错比较难排查，主要错在两个地方：（1）有梯度的稀疏张量不支持 inplace 的修改操作；（2）有梯度的稀疏张量不可以作为 linear 操作的输入（无梯度的稀疏张量是可以的，因为之前讲无梯度稀疏特征的 dropout 操作，案例一律都用的无梯度稀疏张量作为 linear 操作的输入）。通过修改上述错误逻辑，可以得到多层感知机代码如下所示：


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        indices, values = x.indices(), x.values()
        values = self.dropout(values)
        x = torch.sparse_coo_tensor(indices, values, x.shape)
        x = x.to_dense()
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

多层感知机修改完成之后，运行程序，结果如下图所示。

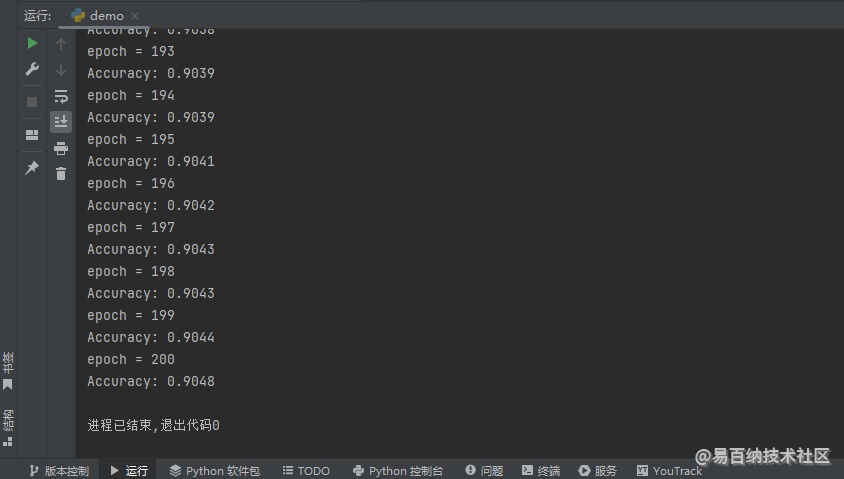
易百纳社区

一切正常，关于有梯度稀疏特征的 dropout 操作可能大家还会有一个问题，就是通过 sparse_coo_tensor 函数构造新的稀疏张量的时候为什么没有指定参数 requires_grad=True？难道维持默认值 False 之前产生的梯度不会丢掉吗？答案一定是不会，我们可以在通过 sparse_coo_tensor 函数构造新的稀疏张量的下面添加一行输出，代码如下：


class MLP(nn.Module):
    def __init__(self, in_features, n_class):
        super().__init__()
        self.dropout = nn.Dropout(0.5)
        self.linear0 = nn.Linear(in_features, 32)
        self.linear1 = nn.Linear(32, n_class)
        self.relu = nn.ReLU(True)

    def forward(self, x):
        indices, values = x.indices(), x.values()
        values = self.dropout(values)
        x = torch.sparse_coo_tensor(indices, values, x.shape)
        print(x.grad_fn)if self.training else None
        x = x.to_dense()
        x = self.relu(self.linear0(x))
        return self.linear1(self.dropout(x))

这里我通过访问稀疏张量 x 的 grad_fn 属性来获取它的导函数，如果它不是 None，说明用 sparse_coo_tensor 函数构造新的稀疏张量不会让梯度消失。运行程序，结果如下图所示。

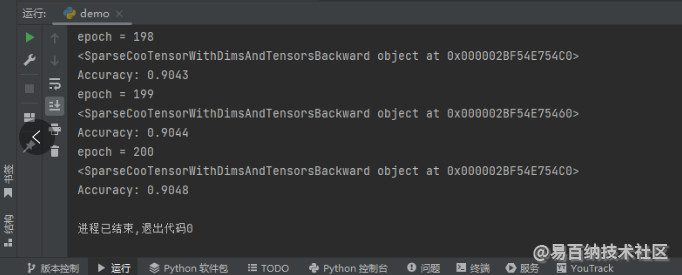
易百纳社区

我们可以发现，x 的 grad_fn 属性显然不是 None，即使没有在构造 COO 格式稀疏张量的 sparse_coo_tensor 函数中声明参数 requires_grad=True，梯度依然不会消失。

结论

通过以上分析，可以得出以下结论：

  1. 稀疏特征的 dropout 操作只有针对非零元素才能确保训练期间的数学期望和测试期间的数学期望一致。
  2. PyTorch 中的 COO 格式的稀疏张量的非零元素可以通过原地修改 values 方法的返回值被原地修改。
  3. 对于无梯度稀疏特征的 dropout 操作，可以使用 inplace 操作来避免创建不必要的中间变量。
  4. 对于有梯度稀疏特征的 dropout 操作，其中的子操作不能含有 inplace 的修改操作。
  5. 有梯度的稀疏张量不可以作为 linear 操作的输入。
  6. 当通过 sparse_coo_tensor 创建新的稀疏张量的时候，即使不指定参数 requires_grad=True（换句话说，用默认值 False），构造出来的稀疏张量的梯度不会消失。

文章转载自公众号：Python机器学习算法说书人

声明：本文内容由易百纳平台入驻作者撰写，文章观点仅代表作者本人，不代表易百纳立场。如有内容侵权或者其他问题，请联系本站进行删除。
小菜很菜
红包 点赞 收藏 评论 打赏
  • 分享
  • 举报
评论
0个
时间排序
内容存在敏感词
手气红包
    易百纳技术社区暂无数据
相关专栏
关于作者
小菜很菜

小菜很菜

暂无个性签名~

原创22
阅读9.4k
收藏1
点赞4
评论0
TA最新文章
打赏用户 共 0 位
我要创作
分享技术经验，可获取创作收益
分类专栏
热门专栏
置顶时间设置
结束时间
删除原因
  • 广告/SPAM
  • 恶意灌水
  • 违规内容
  • 文不对题
  • 重复发帖
打赏作者
易百纳技术社区
小菜很菜
您的支持将鼓励我继续创作！
打赏金额：
￥1易百纳技术社区
￥5易百纳技术社区
￥10易百纳技术社区
￥50易百纳技术社区
￥100易百纳技术社区
支付方式：
微信支付
支付宝支付
易百纳技术社区微信支付
易百纳技术社区
打赏成功!

感谢您的打赏，如若您也想被打赏，可前往 发表专栏 哦~

举报反馈

举报类型

  • 内容涉黄/赌/毒
  • 内容侵权/抄袭
  • 政治相关
  • 涉嫌广告
  • 侮辱谩骂
  • 其他

详细说明

审核成功

发布时间设置
立即发布
延迟发布
发布时间：
是否关联周任务-专栏模块
是
否

审核失败

失败原因
备注
拼手气红包 红包规则
祝福语
恭喜发财，大吉大利！
红包金额
元
红包最小金额不能低于5元
红包数量
个
红包数量范围10~50个
余额支付
当前余额：
可前往问答、专栏板块获取收益 去获取
取 消 确 定

小包子的红包

恭喜发财，大吉大利

红包规则
开

已领取20/40，共1.6元 红包规则

    易百纳技术社区