使用 Scikit-Learn 构建线性回归模型 - 第 1 部分

在 Python 中使用 Scikit-Learn 构建机器学习模型的分步说明

准备好冒险了吗？

Scikit-Learn 是一个用于 Python 数据挖掘和数据分析的机器学习库。Scikit-learn 旨在与数值和科学 Python 库 Numpy 和 Scipy 进行互操作。

我们将创建一个简单的线性回归模型，对其进行训练和测试，使用该模型并最终使用不同的评估指标评估该模型。

Scikit-learn 使用简单的普通最小二乘法来解决这个问题。

普通最小二乘法 (OLS)

OLS 是一种在线性回归模型中估计未知参数的方法。OLS 通过最小化目标因变量与线性函数预测的差值的平方和来选择一组解释变量的线性函数的参数。换句话说，它试图最小化目标变量 (y) 与我们对数据集中所有样本的预测输出之间的误差平方和 (SSE) 或均方误差 (MSE)。

OLS 可以使用以下方法找到最 佳参数：

- 使用封闭式方程分析求解模型参数

- 使用优化算法（梯度下降、随机梯度下降、牛顿法等）

简单回归模型

线性回归拟合具有系数的线性模型，以最小化数据集中实际值 y 与使用线性近似的预测值之间的残差平方和。

在本文的这一部分，我们将使用 OLS 开发一个简单的线性回归模型。

为此，你可以从我的 Github 存储库下载数据集：https://github.com/neslihanvsr/scikit-learn_linear_regression

其中包含汽车特定型号的油耗评级，以及在加拿大零售的新型轻型汽车的预估二氧化碳排放量。

了解数据

# Variables:
# Model Year e.g. 2014
# Make e.g. Acura
# Model e.g. ILX
# Vehicle Class e.g. SUV
# Engine Size e.g. 4.7
# Cylinders e.g 6
# Transmission e.g. A6
# Fuel e.g. Z
# Fuel Consumption City (L/100 km) e.g. 9.9
# Fuel Consumption Hwy (L/100 km) e.g. 8.9
# Fuel Consumption (L/100 km) e.g. 9.2
# Fuel Consumption (mpg) e.g. 33
# CO2 Emissions (g/km) e.g. 182 --> low --> 0
# CO2 Rating e.g. 6
# Smog Rating e.g. 3

# df.head()
#   Model Year   Make              Model Vehicle Class  Engine Size  Cylinders Transmission Fuel  Fuel Consumption City  Fuel Consumption Hwy  Fuel Consumption  Fuel Consumption Comb_mpg  CO2 Emissions  CO2 Rating  Smog Rating
#0        2022  Acura                ILX       Compact         2.40          4          AM8    Z                   9.90                  7.00              8.60                         33            200           6            3
#1        2022  Acura         MDX SH-AWD    SUV: Small         3.50          6         AS10    Z                  12.60                  9.40             11.20                         25            263           4            5
#2        2022  Acura         RDX SH-AWD    SUV: Small         2.00          4         AS10    Z                  11.00                  8.60              9.90                         29            232           5            6
#3        2022  Acura  RDX SH-AWD A-SPEC    SUV: Small         2.00          4         AS10    Z                  11.30                  9.10             10.30                         27            242           5            6
#4        2022  Acura         TLX SH-AWD       Compact         2.00          4         AS10    Z                  11.20                  8.00              9.80                         29            230           5            7

解决方案 1：使用 Scikit-Learn 进行简单线性回归

安装和导入

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

pd.set_option('display.float_format', lambda x: '%.2f' % x)
pd.set_option('display.max_columns', None)
pd.set_option('display.width', 500)

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.model_selection import train_test_split, cross_val_score

读取数据

df = pd.read_csv(r"data/Fuel_Consumption_Ratings.csv")

探索性数据分析

df.head()
df.describe().T
df.isnull().any()
df_ = df[['Engine Size','Cylinders','Fuel Consumption', 'CO2 Emissions']]
df_.head()

df_.hist()
plt.show()

让我们绘制每一个特征

plt.scatter(df_['Fuel Consumption'], df_['CO2 Emissions'], color='red')
plt.xlabel("Fuel Consumption")
plt.ylabel("CO2 Emissions")
plt.show()

plt.scatter(df_['Engine Size'], df_['CO2 Emissions'], color='blue')
plt.xlabel("Engine Size")
plt.ylabel("CO2 Emissions")
plt.show()

plt.scatter(df_['Cylinders'], df_['CO2 Emissions'], color='black')
plt.xlabel("Cylinders")
plt.ylabel("CO2 Emissions")
plt.show()

创建训练和测试数据集

训练和测试拆分涉及将数据集拆分为互斥的训练和测试集。之后，你使用训练集进行训练并使用测试集进行测试。这将对样本外准确性提供更准确的评估，因为测试数据集不是用于训练模型的数据集的一部分。

因此，它让我们更好地了解我们的模型对新数据的泛化能力。由于此数据尚未用于训练模型，因此模型不知道这些数据点的结果。这就是为什么它是样本外测试的原因。

在这里，我们首先创建一个我们认为存在于燃料消耗和 CO2 排放之间的线性关系的模型，然后用图表评估回归。

X = df_[['Fuel Consumption']]
y = df_[['CO2 Emissions']]

模型

reg_model = LinearRegression().fit(X, y)

系数的计算

print ('Intercept: ',reg_model.intercept_)    #17.41832581
print ('Coefficients: ', reg_model.coef_[0])  #21.80188686

预测

26.10 单位的油耗预计会产生多少二氧化碳排放量？

reg_model.intercept_[0] + reg_model.coef_[0][0]*26.10  #586.4475729069786

绘图输出

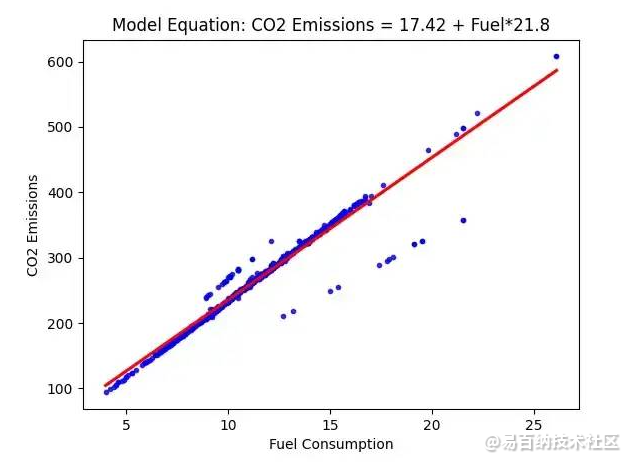
g = sns.regplot(x=X, y=y, scatter_kws={'color': 'b', 's':9},
                 ci=False, color='r')  #güven aralığı false, yani ekleme
g.set_title(f'Model Equation: CO2 Emissions = {round(reg_model.intercept_[0], 2)} + Fuel*{round(reg_model.coef_[0][0], 2)}')
g.set_ylabel('CO2 Emissions')
g.set_xlabel('Fuel Consumption')
plt.show()

模型评估

我们比较实际值和预测值来计算回归模型的准确性。评估指标在模型开发中起着关键作用，因为它提供了对需要改进的领域的洞察力。

有不同的模型评估指标，比如这里的 MSE 是根据测试集计算我们模型的准确性：

平均绝对误差

它是误差绝对值的平均值。这是最容易理解的指标，因为它只是平均误差。

均方误差 (MSE)

均方误差 (MSE) 是平方误差的平均值。它比平均绝对误差更受欢迎，因为重点更倾向于大误差。这是由于与较小的误差相比，平方项以指数方式增加较大的误差。

均方根误差 (RMSE)

R 平方是衡量回归模型性能的流行指标。它表示数据点与拟合回归线的接近程度。R 平方值越高，模型越适合你的数据。最好的分数是 1.0，它可以是负数（因为模型可以任意变差）。

让我们用这些指标评估我们的模型！

# MSE
y_pred = reg_model.predict(X)
mean_squared_error(y, y_pred)
# 229.99811521450823
y.mean() #260.11
y.std() #64.78

# RMSE
np.sqrt(mean_squared_error(y, y_pred))
# 15.165688748438306

# MAE
mean_absolute_error(y, y_pred)
# 6.258727993638971

# MAE
mean_absolute_error(y, y_pred)
# 6.258727993638971

在这一部分中，我们开发了一个简单的线性回归模型来表示我们认为存在于燃料消耗和 CO2 排放之间的线性关系。

在第二部分中，我们将开发 CO2 排放与不同变量之间的多元回归模型。

文章转载自公众号：机器学习算法与知识图谱