机器学习笔记——Kmeans聚类
算法介绍
K-means聚类算是机器学习无监督学习的经典算法了,最早接触的时候是在数模比赛中,那个时候还只停留在使用API上,对K-means算法的核心步骤没有完全搞懂,本文打算详细介绍K-means聚类算法,并给出选择k值的两个方法:手肘法和轮廓系数法,以及所有的code。
K-means原理
原理非常简单,在了解Kmeans算法之前,得知道什么是无监督学习,在机器学习中,无监督学习和有监督学习是两个领域,它们最大得差别就是无监督学习没有标签y,也就是说无监督学习的数据集只包含X,也就是特征数据集,而无监督学习的目的就是找到没有标签y的情况下数据的分布规律以及实用价值。而无监督学习除了聚类还有很多,例如降维、异常值检测,密度估计等。
对于给定的样本集 D = x 1 , x 2 , ⋯ , xm,K-means算法(又叫K均值算法)的目的在于找到簇划分 C=C1,C2,⋯,Ck,使得误差函数 E E E最小。
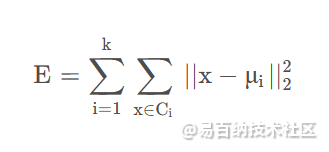

既然找到了学习的目标,我们就想着如何求解上面的模型了。但是求解这个模型并不简单,在所有样本点中找到最合适的簇,这是一个NP难问题,求解非常麻烦,于是我们可以采用一种近似的方法求解,即贪心策略,也就是我们今天要学习的K-means最重要的部分。
下面是K-means算法的步骤
输入:样本集 D={x1,x2,⋯,xm} 聚类簇数
从样本集 D 中随机选择 k k k个样本作为初始均值向量 {μ1,μ2,⋯,μi}
遍历所有样本点,计算 xj 到各个均值向量 μi 之间的距离 dji,选择 dji最小的均值向量的簇标记 k,然后将样本 xj划入相应的簇中。
更新均值向量。
如果当前所有的均值向量的值未改变,则结束算法。输出:簇划分C={C1,C2,⋯Ck}
看起来是不是很简单的一个算法,要注意其中的 dij是通过定义的距离函数计算得到的,如果我们选择不同的距离函数,那么我们得到的 dij 也是不一样的。
常见的距离函数有欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离等等,另外值得注意的是,这里的距离函数只用于解决连续性属性,在面对类别属性时,我们一般采用其它距离函数。
常见的连续性属性的距离函数定义如下:
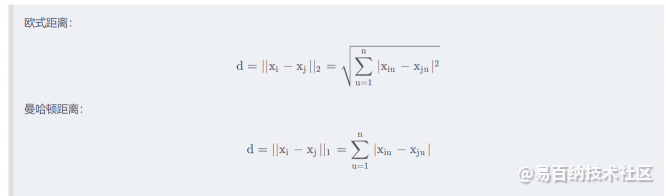
离散属性的定义如下:
令 mu,a表示在属性 u 上取值为 a 的样本数, mu,a,i表示在第 i 个样本簇中在属性 u 上取值为 a 的样本数, k 为样本簇数,则属性 u 上两个离散值 a 和 b 之间的
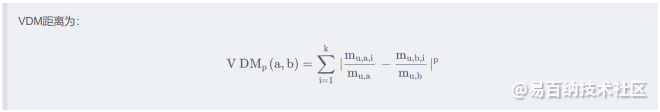
于是得到了K-means算法在处理离散属性时所采用的距离公式。 于是可以将处理离散属性和处理连续属性的距离函数结合起来,构成如下的形式:
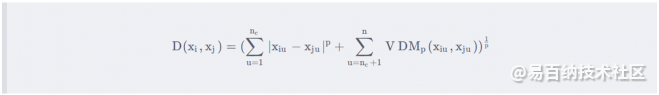
上述 nc和 n−nc分别表示离散属性和连续属性的个数。
此外还需要强调的是,K-means计算样本距离的数据必须是经过归一化之后的数据,因为不同量纲下的数据其大小不在一个维度,所以必须去除量纲对训练的影响。
在实战前,还有一个很重要的点没有介绍,那就是K值的选取,作为K-means算法最重要也是唯一的参数,K值的选取直接影响着K-means聚类结果的好坏,在选择最优K值时,一般有两种方法:手肘法和轮廓系数法。
手肘法选择K值
手肘法的思想非常简单,就是通过判断不同的K值其聚类效果的好坏,从而选择最优的K值,评判聚类好坏的标准我们前面已经介绍过了,那就是E,对于不同的K值,我们采用贪心算法求解得到聚类结果,然后计算当前聚类结果的误差大小,绘制误差随着K值的变化图,其实我们可以猜到,随着K值的增大,E的值应该是越来越小的,因为更多的聚类簇数可以让数据更加分散,这样可以减小E的值。例如我们 实例中得到的手肘图如下:
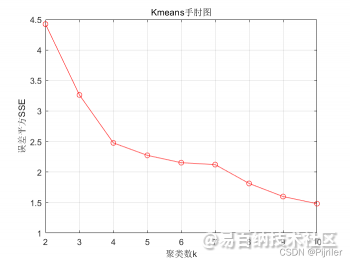
从手肘图上可以明显看出,当误差SSE在聚类数K等于4时存在一个小小的突变,在4之前,误差的下降速度非常快,在4之后,误差下降的速度比较慢,从而构成“手肘状”,这个聚类数4就是我们要找到最优聚类数K。
其实要想理解其原理很简单,随着聚类数K值的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差E自然会变小,并且,当K值小于真实的聚类数时,再增加K所得到的聚合程度回报效果会迅速减小,所以误差的下降幅度就会减小,这就是手肘法的思想。
轮廓系数法
轮廓系数法相较于手肘法来说,我觉得其更据理论性。具体如下:
在手肘法中,我们想找到最优的K值,无非是找到一个合适的评价指标,从评价指标的值来决定最优的K值,而轮廓系数就是轮廓系数所用到的评价指标。轮廓系数的定义如下:
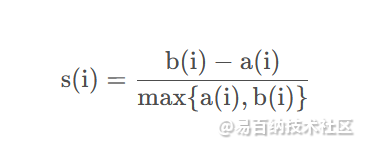
上式中, a(i) 为样本到同簇其它样本点的平均距离,a(i) 越小,说明样本 i i i越应该被聚类到此簇,因而也将 a(i) 的值称为样本 i i i的簇内不相似度。 b(i) 是样本 i i i到其它所有簇样本的平均距离最大值,也就是说为了计算 b(i) ,得先要计算样本 i 到其它簇 j j j的平均距离 bij,然后 b(i)=min{bi1,bi2,⋯,bik}, b ( i ) b(i) b(i) 反映的是样本 i 的簇间不相似度,而我们的目的就是找到使得 b(i) 大,使得 a(i) 小的最优聚类数K,于是把 b(i) 和 a(i) 结合得到s(i) ,分母的 max{a(i),b(i)} 应该是将 s(i) 标准化。我理解的是,不同的K值,其 a(i) 和 b(i) 的变化非常大,这样不容易比较,而除以 a(i) 和 b(i) 的最大值,方便比较不同K值情况下的优劣程度,我们将所有样本的 s(i) 求平均值称为轮廓系数。而且可以看出,轮廓系数的取值范围应该是[-1,1],轮廓系数越大,K值越优,绘制轮廓系数随聚类数K值的变化图如下:
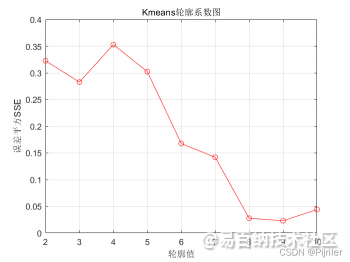
很明显,最优的K值为4,上述的手肘图和轮廓系数图都是一个问题绘制的结果图,两种方法都能看出,当K值等于4时整体的聚类效果最优。
实战
实战部分,我用的是西瓜书上的数据集,因为是二维的好画图,所以作为实战比较好。代码如下:
K-means函数代码
function [results,Mean_vector] = Kmeans(D,k)%{solve 进行K均值聚类Input D——样本训练集 k——聚类的k值Output results——聚类的结果 Mean_vector——均值向量%}% 判断参数的输入是否正确if nargin < 2 error(message('stats:kmeans:TooFewInputs'));end% 获取样本总数量和样本维数[Sample_number,~] = size(D);% 随机选择k个样本作为初始均值向量Random = randperm(Sample_number);Randindex = Random(1:k);Mean_vector = D(Randindex,:);% 定义初始的样本分类存储D_index = zeros(Sample_number,1);% 算法进入循环Until_flag = 0;while(Until_flag ~= k) Distance = zeros(Sample_number,k); % 更新样本归类 for i =1:Sample_number % 计算样本i与各均值向量的的距离 for j =1:k Distance(i,j) = norm(D(i,:)-Mean_vector(j,:)); end % 记录第i个样本的均值归类 [~,min_index] = min(Distance(i,:)); D_index(i) = min_index; end % 更新均值向量 Mean_vector_new = zeros(size(Mean_vector)); Until_flag = 0; for i = 1:k % 获得第i各均值类别中的样本下标a [a,~] = find(D_index == i); Mean_vector_new(i,:) = mean(D(a,:)); if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化 Mean_vector(i,:) = Mean_vector(i,:); Until_flag = Until_flag + 1; else Mean_vector(i,:) = Mean_vector_new(i,:); end endend% 输出结果results = D_index;end
<手肘法代码
function Kmeans_Elbow(D,n)%{solve Kmeans手肘法选择最优K值Input D——训练数据集 n——最大迭代的k值,默认是10Output 绘制结果图%}% 当只输入一个变量时,此时的最大迭代k值默认为10if (nargin<2) n = 10;end% 算法主体Elbow = zeros(n-1,1);% 遍历所有的k值for k = 2:n % 获取样本总数量 [Sample_number,~] = size(D); % 随机选择k个样本作为初始均值向量 Random = randperm(Sample_number); Randindex = Random(1:k); Mean_vector = D(Randindex,:); % 定义初始的样本分类存储 D_index = zeros(Sample_number,1); % 定义循环结束标志 Until_flag = 0; while(Until_flag ~= k) Distance = zeros(Sample_number,k); % 更新样本归类 for i =1:Sample_number % 计算样本i与各均值向量的的距离 for j =1:k Distance(i,j) = norm(D(i,:) - Mean_vector(j,:)); end % 记录第i个样本的均值归类 [~,min_index] = min(Distance(i,:)); D_index(i) = min_index; end % 更新均值向量 Mean_vector_new = zeros(size(Mean_vector)); Until_flag = 0; for i = 1:k % 获得第i各均值类别中的样本下标a [a,~] = find(D_index == i); % 当类别中只有一个样本时,则此样本为中心向量 if length(a) == 1 Mean_vector_new(i,:) = D(a,:); else Mean_vector_new(i,:) = mean(D(a,:)); end if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化 Mean_vector(i,:) = Mean_vector(i,:); Until_flag = Until_flag + 1; elseif (norm(Mean_vector_new(i,:)) ~= norm(Mean_vector(i,:)))&&(sum(isnan(Mean_vector_new(i,:))) == 0) Mean_vector(i,:) = Mean_vector_new(i,:); end end end % 计算手肘值 for i =1:k % 遍历所有种类 [a,~] = find(D_index == i); % 遍历第i个分类的所有样本,累加手肘值 for q = 1:length(a) Elbow(k-1) = Elbow(k-1) + norm(D(a(q),:) - Mean_vector(i,:)); end endend% 对手肘数据进行可视化plot(2:n,Elbow,'ro-')grid onylabel('误差平方SSE')xlabel('聚类数k')title('Kmeans手肘图')end
<轮廓系数法代码
function Kmeans_Silhouette_Coefficient(D,n)%{solve Kmeans轮廓系数法找k值Input D——训练数据集 n——最大迭代的k值,默认是10Output 绘制结果图原理:轮廓系数最大时对应的k值就是最优k值,说明簇内距离小,簇外距离大%}% 当只输入一个变量时,此时的最大迭代k值默认为10if (nargin<2) n = 10;end% 算法主体Coefficient = zeros(n-1,1);% 遍历所有的k值for k = 2:n % 获取样本总数量 [Sample_number,~] = size(D); % 随机选择k个样本作为初始均值向量 Random = randperm(Sample_number); Randindex = Random(1:k); Mean_vector = D(Randindex,:); % 定义初始的样本分类存储 D_index = zeros(Sample_number,1); % 定义循环结束标志 Until_flag = 0; while(Until_flag ~= k) Distance = zeros(Sample_number,k); % 更新样本归类 for i =1:Sample_number % 计算样本i与各均值向量的的距离 for j =1:k Distance(i,j) = norm(D(i,:) - Mean_vector(j,:)); end % 记录第i个样本的均值归类 [~,min_index] = min(Distance(i,:)); D_index(i) = min_index; end % 更新均值向量 Mean_vector_new = zeros(size(Mean_vector)); Until_flag = 0; for i = 1:k % 获得第i各均值类别中的样本下标a [a,~] = find(D_index == i); % 当类别中只有一个样本时,则此样本为中心向量 if length(a) == 1 Mean_vector_new(i,:) = D(a,:); else Mean_vector_new(i,:) = mean(D(a,:)); end if norm(Mean_vector_new(i,:)) == norm(Mean_vector(i,:)) % 如果均值向量未发生变化 Mean_vector(i,:) = Mean_vector(i,:); Until_flag = Until_flag + 1; elseif (norm(Mean_vector_new(i,:)) ~= norm(Mean_vector(i,:)))&&(sum(isnan(Mean_vector_new(i,:))) == 0) Mean_vector(i,:) = Mean_vector_new(i,:); end end end % 计算轮廓系数 % 定义中间变量 a = zeros(Sample_number,1); b = zeros(Sample_number,1); s = zeros(Sample_number,1); for i =1:Sample_number % 计算样本到同簇的平均距离a Temp_index = find((D_index==D_index(i)));% a_ave_i = zeros(length(Temp_index) - 1,1); for j = 1:length(Temp_index) if i~=Temp_index(j) a_ave_i(j) = norm(D(i,:) - D(Temp_index(j),:)); end end a(i) = mean(a_ave_i); % 计算样本到其它簇的所有样本的平均距离 b_temp = zeros(k,1); for j = 1:k if D_index(i) ~= j Temp_index = find(D_index == j); b_ave_i = zeros(length(Temp_index),1); for m = 1:length(Temp_index) b_ave_i(m) = norm(D(i,:) - D(Temp_index(m),:)); end b_temp(j) = mean(b_ave_i); end end b_temp(b_temp == 0) = []; b(i) = min(b_temp); s(i) = (b(i)-a(i))/(max(a(i),b(i))); end % 计算轮廓系数 Coefficient(k-1) = mean(s);end% 对手肘数据进行可视化plot(2:n,Coefficient,'ro-')grid onylabel('误差平方SSE')xlabel('轮廓值')title('Kmeans轮廓系数图')end
<总结
其实本文的K-means算法大致内容已经介绍完毕。还有的一些就是对Kmeans++的改进,既然有改进,那就必须找到现有K-means算法的不足之处。K-means算法的改进版本还是很多的,有K-means++、MinibatchK-means、加速K-means等等,其中我习惯用的就是K-means++,该改进算法与其它改进算法的侧重点有不同点,常规K-means算法在选择初始簇心时的不足,改进常规的随机选择,使用一种启发式方法来选择簇心,这个启发式方法就是轮盘赌法。剩下的就不一一介绍了。
至于K-means算法的应用方面,我觉得最大的用处还是对原始数据进行聚类,虽然可以用到数据预处理和半监督学习上去,但是效果其实并不是很好(个人看法)。
- 分享
- 举报
 暂无数据
暂无数据-
浏览量:747次2023-07-05 10:15:45
-
浏览量:598次2023-07-24 15:23:06
-
浏览量:5050次2021-07-02 14:29:53
-
浏览量:637次2023-09-05 10:02:44
-
浏览量:3191次2020-08-18 11:46:20
-
2023-01-13 11:35:13
-
浏览量:5654次2021-02-09 14:27:57
-
浏览量:919次2023-07-05 10:17:15
-
2023-09-27 11:34:33
-
浏览量:3537次2019-09-18 22:22:32
-
浏览量:2070次2020-08-28 16:40:19
-
浏览量:745次2023-06-02 17:41:00
-
浏览量:6280次2021-06-11 12:41:01
-
浏览量:1458次2024-03-04 14:48:01
-
浏览量:7604次2021-05-06 12:40:38
-
浏览量:707次2023-06-03 15:58:59
-
浏览量:4583次2021-04-19 14:55:34
-
浏览量:845次2023-07-27 11:16:16
-
浏览量:9948次2021-04-20 15:42:26
-
广告/SPAM
-
恶意灌水
-
违规内容
-
文不对题
-
重复发帖
Tony





 微信支付
微信支付举报类型
- 内容涉黄/赌/毒
- 内容侵权/抄袭
- 政治相关
- 涉嫌广告
- 侮辱谩骂
- 其他
详细说明



 微信扫码分享
微信扫码分享 QQ好友
QQ好友






