基于朴素贝叶斯算法对肿瘤类别分类

朴素贝叶斯算法
贝叶斯定理

贝叶斯定理（Bayes Theorem）也称贝叶斯公式，是关于随机 事件的条件概率的定理 定理内容： 如果随机事件A1 ,A2 ,…,An构成样本空间的一个划分（不重、不 漏），且都有正概率，则 对任何一个事件B（P(B)>0），有

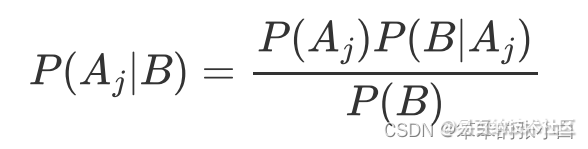
提示： 贝叶斯定理是“由果溯因”的推断，所以计算的是”后验概率”

举例说明：

据天气预报预测，今日下雨(事件A)的概率为50%——P(A)；

堵车（事件B）的概率是80%——P（B）

如果下雨，堵车的概率是95%——P(B|A)

计算：如果放眼望去，已经堵车了，下雨的概率是多少？

根据贝叶斯定理：P(A|B)=0.5x0.95÷0.8=0.59375

朴素贝叶斯算法原理

重要前提条件： 一定要“朴素”—— 样本的各特征之间相互独立

对于待分类样本，在此待分类样本出现的条件下（也就是样本 各个特征已知），计算 各个类别出现的概率，哪个最大就认为此样本属于哪个类别。

详细过程

• 1 设x={a1 ,a2 1 ,…,am}为一个待分类项，而每个a为x的一个特征属性
• 2 有类别集合C={y1 ,y2 2 ,…,yn}
• 3 计算P(y1|x)，P(y2|x)，…，P(yn|x)
• 4 如果P(yk|x)=max{P(y1|x)，P(y2|x)，…，P(yn|x)}，则x∈yk 4

对于第三步的详细计算：

朴素贝叶斯的三种方式

三种朴素贝叶斯的适用条件

• 伯努利朴素贝叶斯

  适用于离散变量，条件是各个特征是服从伯努利分布（0-1分 布），每一个特征的取值 只能有两种值。在scikit-learn中，使用 sklearn.naive_bayes.BernoulliNB实现伯努利朴素 贝叶斯。

• 高斯朴素贝叶斯

  适用于连续变量，条件是各个特征是服从正态分布的。在scikitlearn中，使用 sklearn.naive_bayes.GaussianNB实现高斯朴素贝叶斯。

• 多项式朴素贝叶斯

  适用于离散变量，条件是各个特征是服从多项式分布的，所以每 个特征值不能是负数。 在scikit-learn中，使用sklearn.naive_bayes.MultinomialNB实 现多项式朴素贝叶斯。

补充： 多项式分布来源于统计学中的多项式实验：实验包括n次重 复试验，每项试验都有不同的可能结果。在任何给定的试验 中，特定结果发生的概率是不变的

实战——肿瘤类别的分类

数据集简介

威斯康星乳腺肿瘤数据集是一个非常经典的用于医疗病情分析 的数据集，它包括569个 病例的数据样本，每个样本具有30个特征，而样本共分为两类：恶 性（Malignant）、良性 （Benign）。 使用sklearn.datasets.load_breast_cancer加载数据集 。

使用高斯朴素贝叶斯分类

由于数据集的各个特征属于连续型变量（半径、表面积、平滑 度等），所以使用高斯朴 素贝叶斯(GaussianNB)进行分类。

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()  # 加载威斯康星乳腺肿瘤数据集
# 拆分数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(cancer.data,cancer.target,random_state=666)
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train,y_train)  # 训练集上拟合
gnb.score(X_test,y_test)  # 测试集上测试