Python实现因子分析（附案例实战）_专栏

因子分析

因子分析（Factor Analysis）是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。

例如，在企业形象或品牌形象的研究中，消费者可以通过一个由24个指标构成的评价体系评价百货商城的24个方面的优劣。但消费者主要关心三个方面，即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量找出反映商店环境、商店服务水平和商品价格的3个潜在的因子，对商店进行综合评价。

这3个公共因子可以表示为:

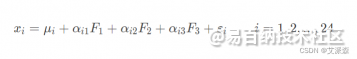
1.因子分析与主成分分析的区别

主成分分析仅仅是变量变换，而因子分析需要构造因子模型。
因子分析：潜在的假想变量和随机影响变量的线性组合表示原始变量。
主成分分析：原始变量的线性组合表示新的综合变量，即主成分。

因子分析数学模型

假设有P个变量X，有m个因子（m≤p）,则因子分析的数学模型可以表示如下：

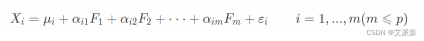
2.因子旋转

若因子分析中得出的各个因子有明确的含义，则因子分析的模型会更加易于解释和有实际意义。在因子分析中可以对因子载荷矩阵进行旋转，使每个变量仅在一个公共因子上有较大的载荷，而在其余的公共因子上的载荷比较小。通过旋转，因子可以有更加明确的含义。常用的一种方法是方差最大旋转。

3.因子得分及其计算

前面我们主要解决了用公共因子的线性组合来表示一组观测变量的有关问题。如果要使用这些因子做其他的研究，比如把得到的因子作为自变量来进行回归分析，对样本进行分类或评价，就需要计算每个个体在每个因子上的得分。

要计算因子得分，需要估计以下表达式：

4.因子分析的步骤

因子分析解决的3个基本问题：

因子载荷阵A的估计
当因子难以得到合理的解释时，对因子载荷阵进行正交变换，即因子旋转。对因子的实际意义做出合理的解释。
给出每个变量（或样品）关于m个公共因子的得分，通常表示为原始变量的线性组合，即因子得分函数。对公共因子做出估计。

因子分析的步骤：

（1）根据问题选取原始变量。

（2）求其相关阵R，探讨其相关性，

（3）从R求解初始公共因子F及其因子载荷矩阵A（主成分法）。

（4）因子旋转，分析因子的含义。

（5）计算因子得分函数。

（6）根据因子得分值进行进一步分析（例如综合评价）。

5.因子分析与主成分分析的区别和联系

（1）因子分析、主成分分析都是重要的降维方法（即数据简化技术），因子分析可以看作主成分分析的推广和发展。

（2）主成分分析不能作为一个模型来描述，它只能作为一般的变量变换，主成分是可观测的原始变量的线性组合。因子分析需要构造因子模型，公共因子是潜在的不可观测的变量，一般不能表示为原始变量的线性组合。

（3）因子分析是用潜在的、不可观测的变量和随机变量的线性组合来表示原始变量，即通过这样的分解来分析原始变量的协方差结构（相依关系）。

6.因子分析案例实战

本次实战数据是一份关于水果茶调查问卷中的一道量表题数据，选项共有9个维度，值范围为1-5

首先导入数据

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei'] #解决中文显示
plt.rcParams['axes.unicode_minus'] = False   #解决符号无法显示
# 导入数据
data = pd.read_csv('data.csv')
data.head()

适用性检验

适用性检验主要是检验数据是否可以使用因子分析，因为因子分析的前提是原始维度之间具有相关性，因此适用性检验就是检验原始维度之间是否具有相关性，如果不相关则不适合做因子分析。

KMO和Bartlett球形检验
主要用的到的方法是KMO和Bartlett球形检验，其中Bartlett球形检验用于检验变量之间是否相关独立，如果p值小于0.05则适合做因子分析；KMO用于检验变量之间的相关性取值在0-1之间，值越大相关性越强。

from factor_analyzer import FactorAnalyzer, calculate_kmo, calculate_bartlett_sphericity
kmo = calculate_kmo(data)
bartlett = calculate_bartlett_sphericity(data)
print(f'KMO:{kmo[1]}')
print(f'Bartlett:{bartlett[1]}')

我们发现KMO值为0.845大于0.6，且 Bartlett值为0<0.05,所以本数据通过适用性检验，可以进一步做因子分析，否则不适合做因子分析。

因子提取

数据原始特征值、方差贡献率

因子提取主要看特征根和解释的总方差

Load_Matrix = FactorAnalyzer(rotation=None, n_factors=len(data.T), method='principal')
Load_Matrix.fit(data)
f_contribution_var = Load_Matrix.get_factor_variance()
matrices_var = pd.DataFrame()
matrices_var["旋转前特征值"] = f_contribution_var[0]
matrices_var["旋转前方差贡献率"] = f_contribution_var[1]
matrices_var["旋转前方差累计贡献率"] = f_contribution_var[2]
matrices_var

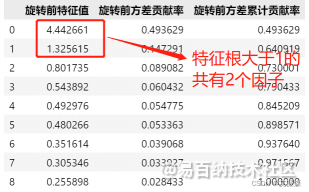
print(Load_Matrix.loadings_)#旋转前的成分矩阵

共因子个数选择，对于公因子的个数选择一般会按照特征根大于1的标准或者累计贡献率设置一个值，本文使用前者作为参考：


eigenvalues = 1
N = 0
for c in matrices_var["旋转前特征值"]:
    if c >= eigenvalues:
        N += 1
    else:
        s = matrices_var["旋转前方差累计贡献率"][N-1]
        print("\n选择了" + str(N) + "个因子累计贡献率为" + str(s)+"\n")
        break

这里选择的两个因子，当然也可以通过图像直观的观察出来


# 主要用来看取多少因子合适，一般是取到平滑处左右，当然还要需要结合贡献率
import matplotlib
matplotlib.rcParams["font.family"] = "SimHei"  
ev, v = Load_Matrix.get_eigenvalues()
print('\n相关矩阵特征值：', ev)
plt.figure(figsize=(8, 6.5))
plt.scatter(range(1, data.shape[1] + 1), ev)
plt.plot(range(1, data.shape[1] + 1), ev)
plt.title('特征值和因子个数的变化', fontdict={'weight': 'normal', 'size': 25})
plt.xlabel('因子', fontdict={'weight': 'normal', 'size': 15})
plt.ylabel('特征值', fontdict={'weight': 'normal', 'size': 15})
plt.grid()
plt.show()

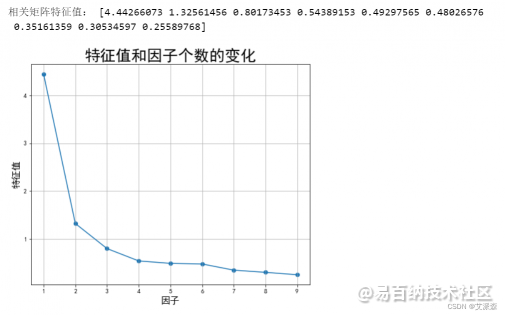
上图也叫碎石图，从图中我们也可以看出应该选择两个公共因子。

通过以上输出的结果可以看出，原始因子之间存在相关性，因子之间没有差异化特征，所以需要进行因子旋转。

因子旋转

目的：使得各因子具有差异化的特征；

使用方法：最大方差法（正交旋转）、斜交旋转（多使用前者）

Load_Matrix_rotated = FactorAnalyzer(rotation='varimax', n_factors=2, method='principal')
Load_Matrix_rotated.fit(data)
f_contribution_var_rotated = Load_Matrix_rotated.get_factor_variance()
matrices_var_rotated = pd.DataFrame()
matrices_var_rotated["特征值"] = f_contribution_var_rotated[0]
matrices_var_rotated["方差贡献率"] = f_contribution_var_rotated[1]
matrices_var_rotated["方差累计贡献率"] = f_contribution_var_rotated[2]
print("旋转后的载荷矩阵的贡献率")
print(matrices_var_rotated)
print("旋转后的成分矩阵")
print(Load_Matrix_rotated.loadings_)

为了直观看出结果，这里可以画一个相关性图形。

import seaborn as sns
import numpy as np
Load_Matrix = Load_Matrix_rotated.loadings_
df = pd.DataFrame(np.abs(Load_Matrix),index= data.columns)
plt.figure(figsize=(8, 8))
ax = sns.heatmap(df, annot=True, cmap="BuPu",cbar=False)
ax.yaxis.set_tick_params(labelsize=15) # 设置y轴字体大小
plt.title("因子分析", fontsize="xx-large")
plt.ylabel("因子", fontsize="xx-large")# 设置y轴标签
plt.show()# 显示图片

因子命名

从上面图像我们可以看出，品质、价格、口味、制作过程透明、服务态度归属到一类因子，我们可以命名为“品质追求型”，将名称、包装、网络热度、品牌效应命名为“品牌效益型”。

因子得分

当因子模型建立后，需要反过来考察一个样品的性质以及样品之间的相互关系，比如当关于企业经济效益的因子模型建立之后，希望知道每一个企业经济效益的优劣，或者把企业进行分类，这个时候就需要进行因子得分计算。

# 计算因子得分（回归方法）（系数矩阵的逆乘以因子载荷矩阵）
f_corr = data.corr()# 皮尔逊相关系数
X1 = np.mat(f_corr)
X1 = np.linalg.inv(X1)
factor_score_weight = np.dot(X1, Load_Matrix_rotated.loadings_)
factor_score_weight = pd.DataFrame(factor_score_weight)
col = []
for i in range(N):
    col.append("factor" + str(i + 1))
factor_score_weight.columns = col
factor_score_weight.index = f_corr.columns
print("因子得分：\n", factor_score_weight)