【深度学习】基于Pytorch多层感知机的高级API实现和注意力机制(三)

@[toc]
1 权重衰减
我们已经描述了过拟合的问题,现在我们可以介绍一些正则化模型的技术。我们总是可以通过去收集更多的训练数据来缓解过拟合。但这可能成本很高而且耗时.或者完全超出我们的控制,在短期内不可能做到。假设已经拥有尽可能多的高质量数据,现在我们将重点放在正则化技术上。
回想一下,在多项式回归的例子中,我们可以通过调整拟合多项式的阶数来限制模型的容量。实际上,限制特征的数量是缓解过拟合的一种常用技术。然而,简单地丢弃特征对于这项工作来说可能过于生硬。我们继续思考多项式回归的例子,考虑高维输入可能发生的情况。多项式对多变量数据的自然扩展称为单项式(monomials),也可以说是变量幂的乘积。单项式的阶数是幂的和。例如,$x_1^2 x_2$和$x_3 x_5^2$都是3次单项式。
注意,随着阶数$d$的增长,带有阶数$d$的项数迅速增加。给定$k$个变量,阶数$d$(即$k$多选$d$)的个数为${k - 1 + d} \choose {k - 1}$。即使是阶数上的微小变化,比如从$2$到$3$,也会显著增加我们模型的复杂性。因此,我们经常需要一个更细粒度的工具来调整函数的复杂性。
1.1 范数
范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,范数是一个函数,是矢量空间内的所有矢量赋予非零的正长度或大小。半范数可以为非零的矢量赋予零长度。 定义范数的矢量空间是赋范矢量空间;同样,定义半范数的矢量空间就是赋半范矢量空间。
1.2 L1范数
L1范数是指向量中各个元素绝对值之和
1.3 L2范数
定义为向量所有元素的平方和的开平方. 对于两个向量,则L2范数可以认为是空间中两个点间的距离.
1.4 范数与权重衰减
权重衰减. 权重衰减等价于L2范数正则化 (regularzation)。 这句话记小本本哦!!!!
在训练参数化机器学习模型时,权重衰减(通常称为$L_2$正则化)是最广泛使用的正则化的技术之一。这项技术是基于一个基本直觉,即在所有函数$f$中,函数$f = 0$(所有输入都得到值$0$)在某种意义上是最简单的,我们可以通过函数与零的距离来衡量函数的复杂度。但是我们应该如何精确地测量一个函数和零之间的距离呢?没有一个正确的答案。事实上,整个数学分支,包括函数分析和巴拿赫空间理论,都在致力于回答这个问题。
一种简单的方法是通过线性函数$f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x}$中的权重向量的某个范数来度量其复杂性,例如$| \mathbf{w} |^2$。要保证权重向量比较小,最常用方法是将其范数作为惩罚项加到最小化损失的问题中。将原来的训练目标最小化训练标签上的预测损失,调整为最小化预测损失和惩罚项之和。 现在,如果我们的权重向量增长的太大,我们的学习算法可能会更集中于最小化权重范数$| \mathbf{w} |^2$。这正是我们想要的。让我们回顾一下线性回归例子。我们的损失由下式给出:
$$L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2.$$
回想一下,$\mathbf{x}^{(i)}$是样本$i$的特征,$y^{(i)}$是样本$i$的标签。$(\mathbf{w}, b)$是权重和偏置参数。为了惩罚权重向量的大小,我们必须以某种方式在损失函数中添加$| \mathbf{w} |^2$,但是模型应该如何平衡这个新的额外惩罚的损失?实际上,我们通过正则化常数$\lambda$来描述这种权衡,这是一个非负超参数,我们使用验证数据拟合:
$$L(\mathbf{w}, b) + \frac{\lambda}{2} |\mathbf{w}|^2,$$
对于$\lambda = 0$,我们恢复了原来的损失函数。对于$\lambda > 0$,我们限制$| \mathbf{w} |$的大小。我们仍然除以$2$:当我们取一个二次函数的导数时,$2$和$1/2$会抵消,以确保更新表达式看起来既漂亮又简单。聪明的读者可能会想知道为什么我们使用平方范数而不是标准范数(即欧几里得距离)。我们这样做是为了便于计算。通过平方$L_2$范数,我们去掉平方根,留下权重向量每个分量的平方和。这使得惩罚的导数很容易计算:导数的和等于和的导数。
此外,你可能会问为什么我们首先使用$L_2$范数,而不是$L_1$范数。事实上,这些选择在整个统计领域中都是有效的和受欢迎的。$L_2$正则化线性模型构成经典的岭回归(ridge regression)算法,$L_1$正则化线性回归是统计学中类似的基本模型,通常被称为套索回归(lasso regression)。
使用$L_2$范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。在实践中,这可能使它们对单个变量中的观测误差更为鲁棒。相比之下,$L_1$惩罚会导致模型将其他权重清除为零而将权重集中在一小部分特征上。这称为特征选择(feature selection),这可能是其他场景下需要的。
$$ \begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned} $$
根据之前章节所讲的,我们根据估计值与观测值之间的差异来更新$\mathbf{w}$。然而,我们同时也在试图将$\mathbf{w}$的大小缩小到零。这就是为什么这种方法有时被称为权重衰减。我们仅考虑惩罚项,优化算法在训练的每一步衰减权重。与特征选择相比,权重衰减为我们提供了一种连续的机制来调整函数的复杂度。较小的$\lambda$值对应较少约束的$\mathbf{w}$,而较大的$\lambda$值对$\mathbf{w}$的约束更大。
是否对相应的偏置$b^2$进行惩罚在不同的实现中会有所不同。在神经网络的不同层中也会有所不同。通常,我们不正则化网络输出层的偏置项。
2 高维线性回归-权重衰减
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
我们[像以前一样生成一些数据],生成公式如下:
($$y = 0.05 + \sum_{i = 1}^d 0.01 x_i + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0, 0.01^2).$$)
我们选择标签是关于输入的线性函数。标签同时被均值为0,标准差为0.01高斯噪声破坏。为了使过拟合的效果更加明显,我们可以将问题的维数增加到$d = 200$,并使用一个只包含20个样本的小训练集。
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)3 代码实现
从头开始实现权重衰减,只需将 𝐿2 的平方惩罚添加到原始目标函数中。
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]定义 𝐿2 范数惩罚
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2定义训练代码实现 下面的代码将模型拟合训练数据集,并在测试数据集上进行评估。线性网络和平方损失没有变化,所以我们通过d2l.linreg和d2l.squared_loss导入它们。唯一的变化是损失现在包括了惩罚项。
def train(lambd):
w, b = init_params()
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
with torch.enable_grad():
# 增加了L2范数惩罚项,广播机制使l2_penalty(w)成为一个长度为`batch_size`的向量。
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
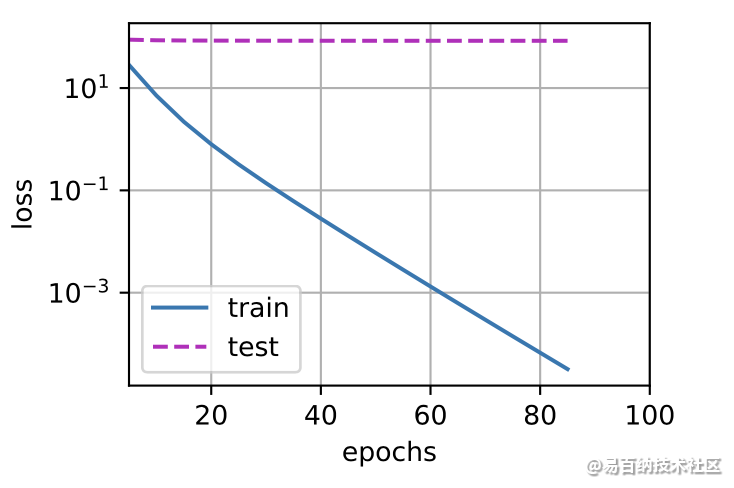
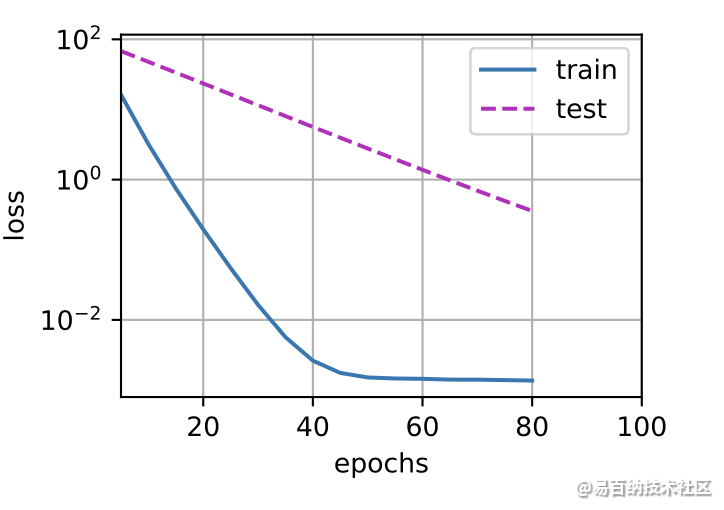
print('w的L2范数是:', torch.norm(w).item())忽略正则化直接训练 我们现在用lambd = 0禁用权重衰减后运行这个代码。注意,这里训练误差有了减少,但测试误差没有减少。这意味着出现了严重的过拟合。这是过拟合的一个典型例子。
train(lambd=0)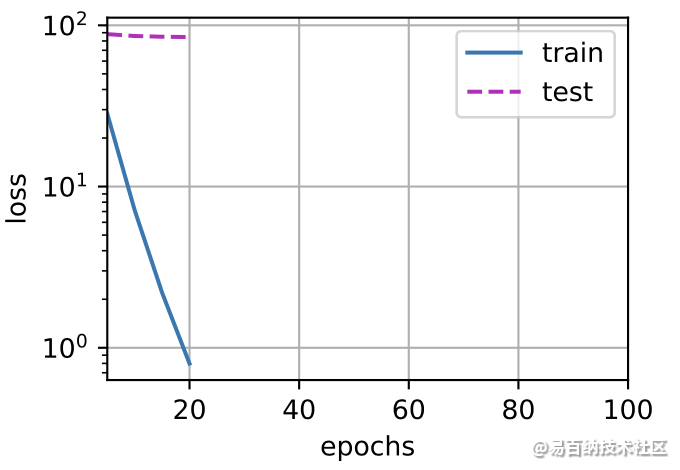
 使用权重衰减
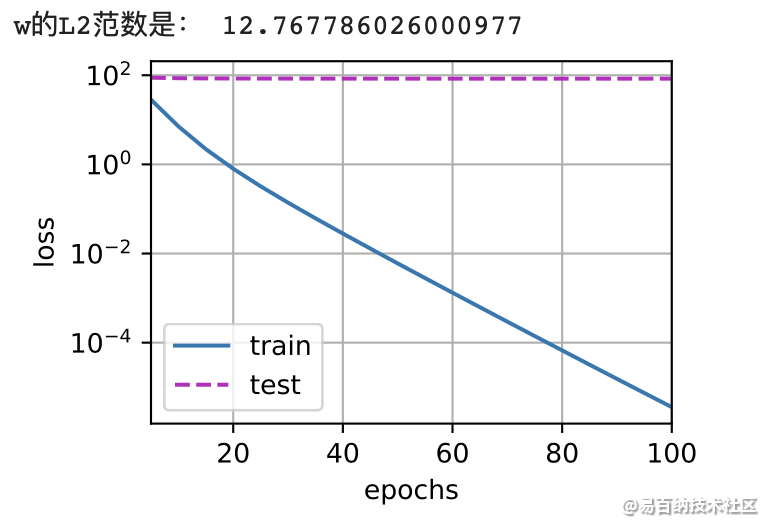
使用权重衰减
train(lambd=3)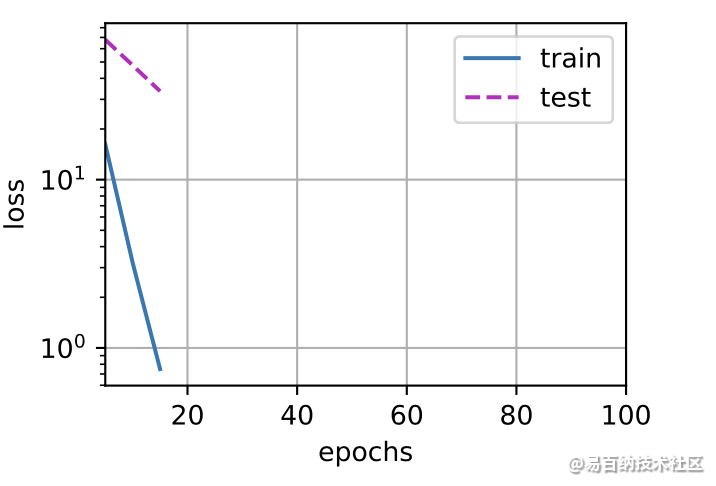
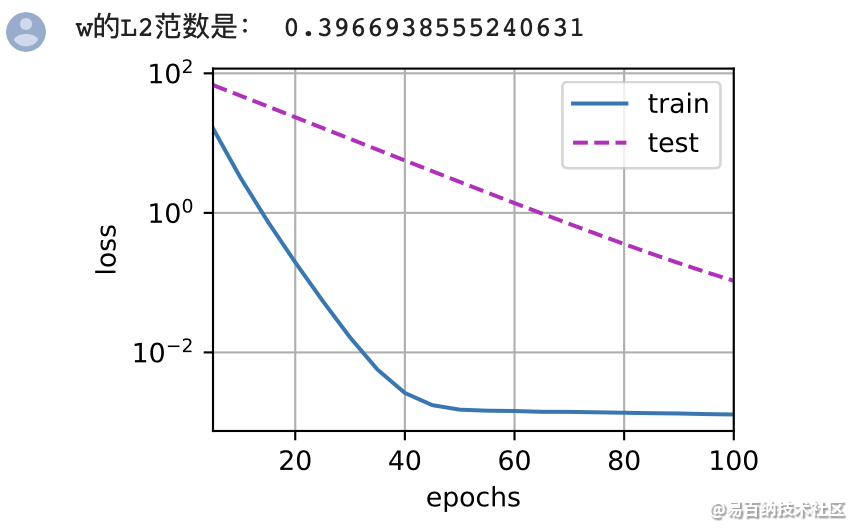 由于权重衰减在神经网络优化中很常用,深度学习框架为了便于使用权重衰减,便将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
由于权重衰减在神经网络优化中很常用,深度学习框架为了便于使用权重衰减,便将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处,允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
在下面的代码中,我们在实例化优化器时直接通过weight_decay指定weight decay超参数。默认情况下,PyTorch同时衰减权重和偏移。这里我们只为权重设置了weight_decay,所以bias参数 𝑏 不会衰减。
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss()
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减。
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
with torch.enable_grad():
trainer.zero_grad()
l = loss(net(X), y)
l.backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())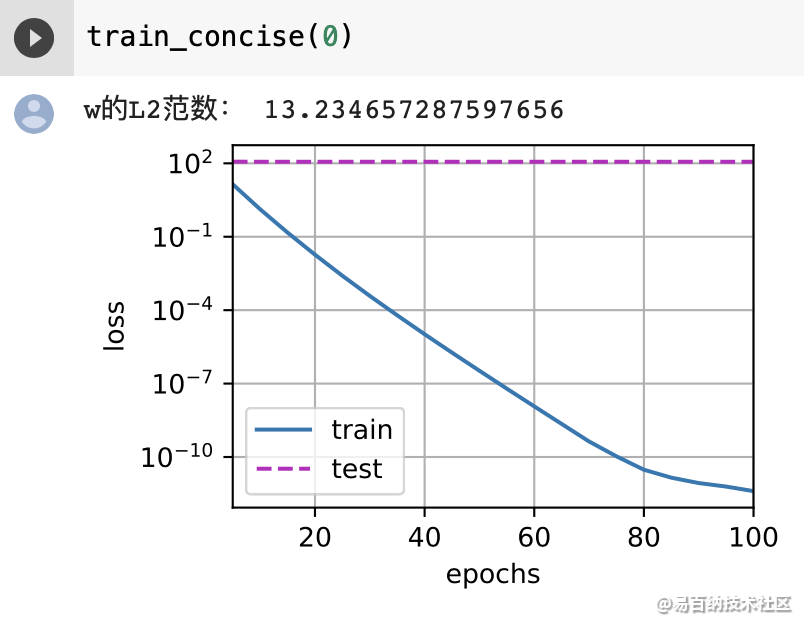
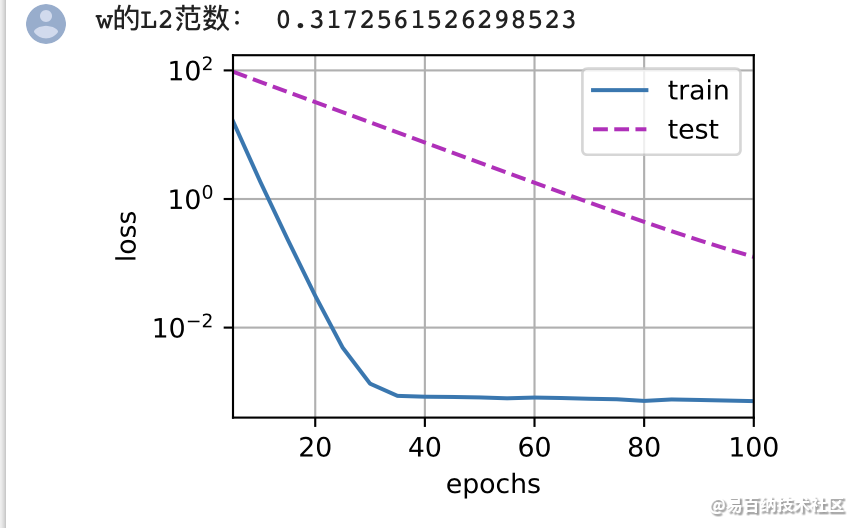
4 总结
- 正则化是处理过拟合的常用方法。在训练集的损失函数中加入惩罚项,以降低学习到的模型的复杂度。
- 保持模型简单的一个特别的选择是使用$L_2$惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。
- 权重衰减功能在深度学习框架的优化器中提供。
- 在同一训练代码实现中,不同的参数集可以有不同的更新行为。
5 Pytorch-BN层详细解读
机器学习领域有个很重要的假设:独立同分布假设,即假设训练数据和测试数据是满足相同分布的。我们知道:神经网络的训练实际上就是在拟合训练数据的分布。如果不满足独立同分布假设,那么训练得到的模型的泛化能力肯定不好。
再来思考一个问题:为什么传统的神经网络要求将数据归一化(训练阶段将训练数据归一化并记录均值和方差,测试阶段利用记录的均值和方差将测试数据也归一化)?
首先:做了归一化之后,可以近似的认为训练数据和测试数据满足相同分布(即均值为0,方差为1的标准正态),这样一来模型的泛化能力会得到提高。其次:如果不做归一化,使用mini-batch梯度下降法训练的时候,每批训练数据的分布不相同,那么网络就要在每次迭代的时候去适应不同的分布,这样会大大降低网络的训练速度。综合以上两点,所以需要对数据做归一化预处理。PS:如果是mini-batch梯度下降法,每个batch都可以计算出一个均值和方差,最终记录的均值和方差是所有batches均值和方差的期望,当然也有其它更复杂的记录方式,如pytorch使用的滑动平均。
Internal Covariate Shift问题:在训练的过程中,即使对输入层做了归一化处理使其变成标准正态,随着网络的加深,函数变换越来越复杂,许多隐含层的分布还是会彻底放飞自我,变成各种奇奇怪怪的正态分布,并且整体分布逐渐往非线性函数(也就是激活函数)的取值区间的上下限两端靠近。对于sigmoid函数来说,就意味着输入值是大的负数或正数,这导致反向传播时底层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因。
为了解决上述问题,又想到网络的某个隐含层相对于之后的网络就相当于输入层,所以BN的基本思想就是:把网络的每个隐含层的分布都归一化到标准正态。其实就是把越来越偏的分布强制拉回到比较标准的分布,这样使得激活函数的输入值落在该激活函数对输入比较敏感的区域,这样一来输入的微小变化就会导致损失函数较大的变化。通过这样的方式可以使梯度变大,就避免了梯度消失的问题,而且梯度变大意味着收敛速度快,能大大加快训练速度。
简单说来就是:传统的神经网络只要求第一个输入层归一化,而带BN的神经网络则是把每个输入层(把隐含层也理解成输入层)都归一化。
Pytorch中的BN操作为nn.BatchNorm2d(self, num_features, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
num_features,输入数据的通道数,归一化时需要的均值和方差是在每个通道中计算的 eps,用来防止归一化时除以0 momentum,滑动平均的参数,用来计算running_mean和running_var affine,是否进行仿射变换,即缩放操作 track_running_stats,是否记录训练阶段的均值和方差,即running_mean和running_var BN层的状态包含五个参数:
weight,缩放操作的γ \gammaγ。 bias,缩放操作的β \betaβ。 running_mean,训练阶段统计的均值,测试阶段会用到。 running_var,训练阶段统计的方差,测试阶段会用到。 num_batches_tracked,训练阶段的batch的数目,如果没有指定momentum,则用它来计算running_mean和running_var。一般momentum默认值为0.1,所以这个属性暂时没用。 weight和bias这两个参数需要训练,而running_mean、running_val和num_batches_tracked不需要训练,它们只是训练阶段的统计值。
- 分享
- 举报
 暂无数据
暂无数据-
浏览量:7050次2021-08-09 16:09:53
-
浏览量:5195次2021-08-09 16:10:30
-
浏览量:6884次2021-06-27 18:19:55
-
浏览量:4632次2021-04-14 16:23:03
-
浏览量:6410次2021-08-03 11:36:18
-
浏览量:6583次2021-08-03 11:36:37
-
浏览量:6003次2021-08-02 09:34:03
-
浏览量:5361次2021-08-05 09:21:07
-
浏览量:5526次2021-08-05 09:20:49
-
浏览量:14753次2021-06-15 10:27:34
-
浏览量:8186次2021-08-10 10:06:51
-
浏览量:6448次2021-07-26 17:43:04
-
浏览量:5404次2021-07-26 11:25:51
-
浏览量:5874次2021-06-23 15:25:25
-
浏览量:5595次2021-08-13 15:39:02
-
浏览量:1134次2023-12-14 16:38:19
-
浏览量:5324次2021-07-26 11:28:05
-
浏览量:7060次2021-04-12 12:54:06
-
浏览量:1392次2024-02-01 14:28:23
-
广告/SPAM
-
恶意灌水
-
违规内容
-
文不对题
-
重复发帖
这把我C





 微信支付
微信支付举报类型
- 内容涉黄/赌/毒
- 内容侵权/抄袭
- 政治相关
- 涉嫌广告
- 侮辱谩骂
- 其他
详细说明


 微信扫码分享
微信扫码分享 QQ好友
QQ好友





