【深度学习】基于Pytorch的softmax回归问题辨析和应用(二)_专栏

【深度学习】基于Pytorch的softmax回归问题辨析和应用(二)

在这里插入图片描述

文章目录

1 softmax回归的实现
    1.1 初始化模型参数
    1.2 Softmax的实现
    1.3 优化器
    1.4 训练
2 多分类问题torch.nn.Softmax的使用

1 softmax回归的实现

我们可以发现(通过深度学习框架的高级API能够使实现)
线性(回归变得更加容易)。同样地，通过深度学习框架的高级API也能更方便地实现分类模型。让我们继续使用Fashion-MNIST数据集，并保持批量大小为256.

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

在这里插入图片描述

1.1 初始化模型参数

在 Sequential 中添加一个带有10个输出的全连接层。同样，在这里，Sequential 并不是必要的，但我们可能会形成这种习惯。因为在实现深度模型时，Sequential将无处不在。我们仍然以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

1.2 Softmax的实现

回想一下，softmax函数 $\hat y_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}$，其中$\hat y_j$是预测的概率分布。$o_j$是未归一化的预测$\mathbf{o}$的第$j$个元素。如果$o_k$中的一些数值非常大，那么 $\exp(o_k)$ 可能大于数据类型容许的最大数字（即上溢（overflow））。这将使分母或分子变为inf（无穷大），我们最后遇到的是0、inf 或 nan（不是数字）的 $\hat y_j$。在这些情况下，我们不能得到一个明确定义的交叉熵的返回值。

解决这个问题的一个技巧是，在继续softmax计算之前，先从所有$o_k$中减去$\max(o_k)$。你可以证明每个 $o_k$ 按常数进行的移动不会改变softmax的返回值。在减法和归一化步骤之后，可能有些 $o_j$ 具有较大的负值。由于精度受限， $\exp(o_j)$ 将有接近零的值，即下溢（underflow）。这些值可能会四舍五入为零，使 $\hat y_j$ 为零，并且使得 $\log(\hat y_j)$ 的值为 -inf。反向传播几步后，我们可能会发现自己面对一屏幕可怕的nan结果。

尽管我们要计算指数函数，但我们最终在计算交叉熵损失时会取它们的对数。
通过将softmax和交叉熵结合在一起，可以避免反向传播过程中可能会困扰我们的数值稳定性问题。如下面的等式所示，我们避免计算$\exp(o_j)$，而可以直接使用$o_j$。因为$\log(\exp(\cdot))$被抵消了。

$$
\begin{aligned}
\log{(\hat y_j)} & = \log\left( \frac{\exp(o_j)}{\sum_k \exp(o_k)}\right) \
& = \log{(\exp(o_j))}-\log{\left( \sum_k \exp(o_k) \right)} \
& = o_j -\log{\left( \sum_k \exp(o_k) \right)}.
\end{aligned}
$$

我们也希望保留传统的softmax函数，以备我们需要评估通过模型输出的概率。
但是，我们没有将softmax概率传递到损失函数中，

loss = nn.CrossEntropyLoss()

1.3 优化器

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

1.4 训练

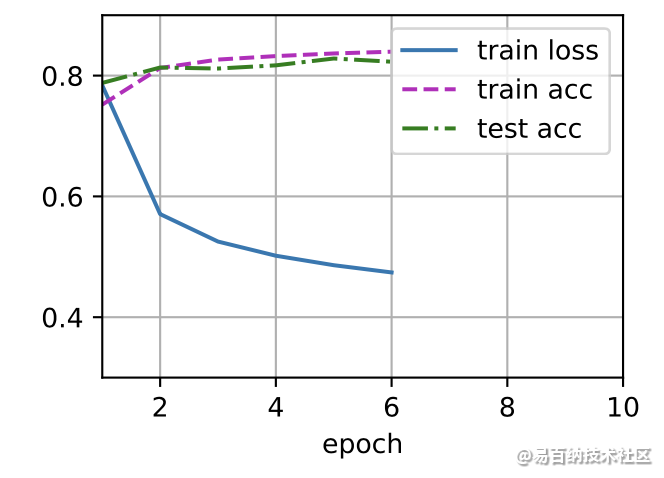
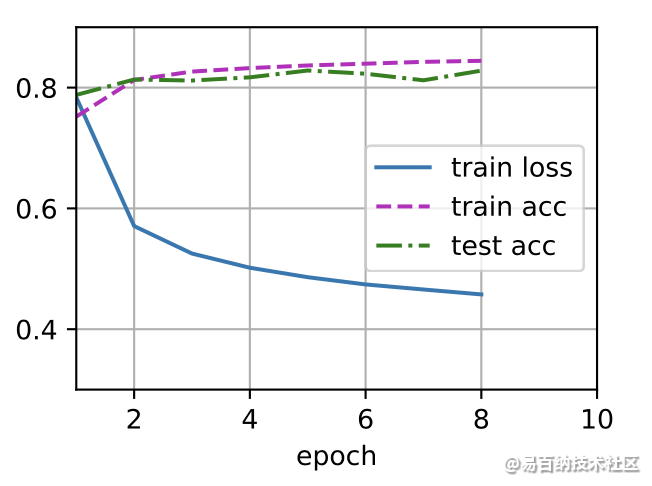
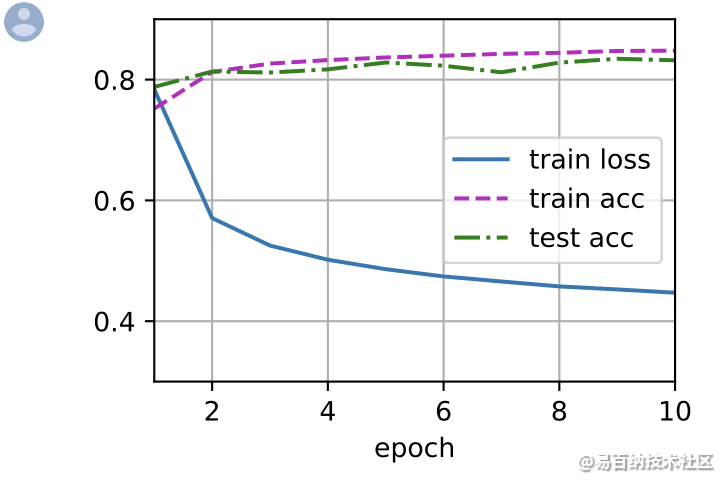
接下来我们实现一个训练函数，它会在train_iter 访问到的训练数据集上训练一个模型net。该训练函数将会运行多个迭代周期（由num_epochs指定）。在每个迭代周期结束时，利用 test_iter 访问到的测试数据集对模型进行评估。我们将利用 Animator 类来可视化训练进度。

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）。"""
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    if isinstance(updater, gluon.Trainer):
        updater = updater.step
    for X, y in train_iter:
        # 计算梯度并更新参数
        with autograd.record():
            y_hat = net(X)
            l = loss(y_hat, y)
        l.backward()
        updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.size)
    # 返回训练损失和训练准确率
    return metric[0] / metric[2], metric[1] / metric[2]

使用SGD优化器更新模型参数：

lr = 0.1
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）。"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)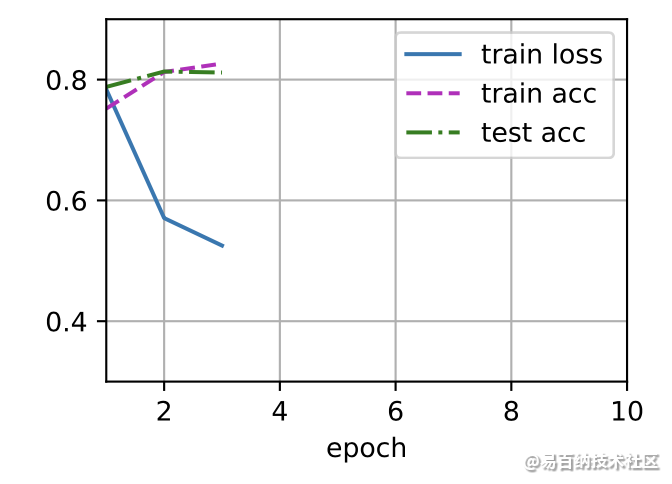

在这里插入图片描述

2 多分类问题torch.nn.Softmax的使用

为什么谈论这个问题呢？是因为我在工作的过程中遇到了语义分割预测输出特征图个数为16，也就是所谓的16分类问题。

因为每个通道的像素的值的大小代表了像素属于该通道的类的大小，为了在一张图上用不同的颜色显示出来，我不得不学习了torch.nn.Softmax的使用。

首先看一个简答的例子，倘若输出为(3, 4, 4)，也就是3张4x4的特征图。

import torch
img = torch.rand((3,4,4))
print(img)

输出为：

tensor([[[0.0413, 0.8728, 0.8926, 0.0693],
         [0.4072, 0.0302, 0.9248, 0.6676],
         [0.4699, 0.9197, 0.3333, 0.4809],
         [0.3877, 0.7673, 0.6132, 0.5203]],

        [[0.4940, 0.7996, 0.5513, 0.8016],
         [0.1157, 0.8323, 0.9944, 0.2127],
         [0.3055, 0.4343, 0.8123, 0.3184],
         [0.8246, 0.6731, 0.3229, 0.1730]],

        [[0.0661, 0.1905, 0.4490, 0.7484],
         [0.4013, 0.1468, 0.2145, 0.8838],
         [0.0083, 0.5029, 0.0141, 0.8998],
         [0.8673, 0.2308, 0.8808, 0.0532]]])

我们可以看到共三张特征图，每张特征图上对应的值越大，说明属于该特征图对应类的概率越大。

import torch.nn as nn
sogtmax = nn.Softmax(dim=0)
img = sogtmax(img)
print(img)

tensor([[[0.2780, 0.4107, 0.4251, 0.1979],
         [0.3648, 0.2297, 0.3901, 0.3477],
         [0.4035, 0.4396, 0.2993, 0.2967],
         [0.2402, 0.4008, 0.3273, 0.4285]],

        [[0.4371, 0.3817, 0.3022, 0.4117],
         [0.2726, 0.5122, 0.4182, 0.2206],
         [0.3423, 0.2706, 0.4832, 0.2522],
         [0.3718, 0.3648, 0.2449, 0.3028]],

        [[0.2849, 0.2076, 0.2728, 0.3904],
         [0.3627, 0.2581, 0.1917, 0.4317],
         [0.2543, 0.2898, 0.2175, 0.4511],
         [0.3880, 0.2344, 0.4278, 0.2686]]])

可以看到，上面的代码对每张特征图对应位置的像素值进行Softmax函数处理，图中标红位置加和=1，同理，标蓝位置加和=1。

我们看到Softmax函数会对原特征图每个像素的值在对应维度(这里dim=0，也就是第一维)上进行计算，将其处理到0～1之间，并且大小固定不变。

print(torch.max(img,0))

输出为：

torch.return_types.max(
values=tensor([[0.4371, 0.4107, 0.4251, 0.4117],
        [0.3648, 0.5122, 0.4182, 0.4317],
        [0.4035, 0.4396, 0.4832, 0.4511],
        [0.3880, 0.4008, 0.4278, 0.4285]]),
indices=tensor([[1, 0, 0, 1],
        [0, 1, 1, 2],
        [0, 0, 1, 2],
        [2, 0, 2, 0]]))

可以看到这里3x4x4变成了1x4x4，而且对应位置上的值为像素对应每个通道上的最大值，并且indices是对应的分类。

清楚理解了上面的流程，那么我们就容易处理了。

看具体案例，这里输出output的大小为：16x416x416.

output = torch.tensor(output)

sm = nn.Softmax(dim=0)
output = sm(output)

mask = torch.max(output,0).indices.numpy()

# 因为要转化为RGB彩色图，所以增加一维
rgb_img = np.zeros((output.shape[1], output.shape[2], 3))
for i in range(len(mask)):
    for j in range(len(mask[0])):
        if mask[i][j] == 0:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 255
            rgb_img[i][j][2] = 255
        if mask[i][j] == 1:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 180
            rgb_img[i][j][2] = 0
        if mask[i][j] == 2:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 180
            rgb_img[i][j][2] = 180
        if mask[i][j] == 3:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 180
            rgb_img[i][j][2] = 255
        if mask[i][j] == 4:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 255
            rgb_img[i][j][2] = 180
        if mask[i][j] == 5:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 255
            rgb_img[i][j][2] = 0
        if mask[i][j] == 6:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 180
        if mask[i][j] == 7:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 255
        if mask[i][j] == 8:
            rgb_img[i][j][0] = 255
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 0
        if mask[i][j] == 9:
            rgb_img[i][j][0] = 180
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 0
        if mask[i][j] == 10:
            rgb_img[i][j][0] = 180
            rgb_img[i][j][1] = 255
            rgb_img[i][j][2] = 255
        if mask[i][j] == 11:
            rgb_img[i][j][0] = 180
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 180
        if mask[i][j] == 12:
            rgb_img[i][j][0] = 180
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 255
        if mask[i][j] == 13:
            rgb_img[i][j][0] = 180
            rgb_img[i][j][1] = 255
            rgb_img[i][j][2] = 180
        if mask[i][j] == 14:
            rgb_img[i][j][0] = 0
            rgb_img[i][j][1] = 180
            rgb_img[i][j][2] = 255
        if mask[i][j] == 15:
            rgb_img[i][j][0] = 0
            rgb_img[i][j][1] = 0
            rgb_img[i][j][2] = 0

cv2.imwrite('output.jpg', rgb_img)

在这里插入图片描述