【深度学习】基于Pytorch的线性模型概念辨析和实现(二)

@[toc]

1 线性回归的从零开始实现

安装包：

!pip install git+https://github.com/d2l-ai/d2l-zh@release  # installing d2l

%matplotlib inline
import random
import torch
from d2l import torch as d2l

生成数据集 为了简单起见，我们将[根据带有噪声的线性模型构造一个人造数据集。] 我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。 我们将使用低维数据，这样可以很容易地将其可视化。 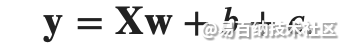你可以将 𝜖 视为捕获特征和标签时的潜在观测误差。在这里我们认为标准假设成立，即 𝜖 服从均值为0的正态分布。 为了简化问题，我们将标准差设为0.01。下面的代码生成合成数据集。

def synthetic_data(w, b, num_examples):  #@save
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
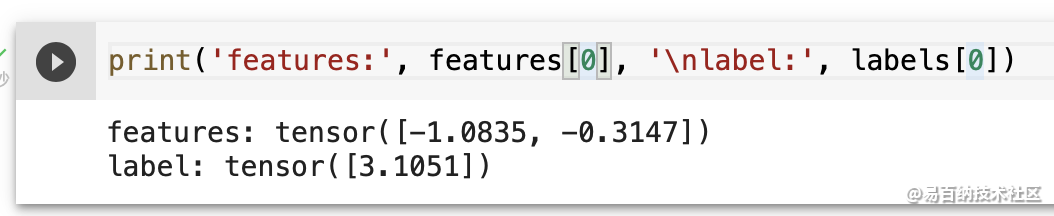
features, labels = synthetic_data(true_w, true_b, 1000)

注意，[features 中的每一行都包含一个二维数据样本，labels 中的每一行都包含一维标签值（一个标量）]。

d2l.set_figsize()
d2l.plt.scatter(features[:, (1)].detach().numpy(),
                labels.detach().numpy(), 1);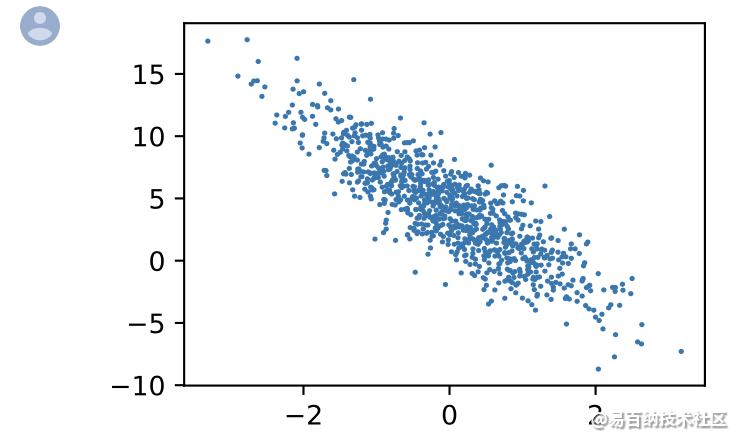

读取数据集

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i +
                                                   batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

(初始化模型参数)

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

(定义模型)

def linreg(X, w, b):  #@save
    """线性回归模型。"""
    return torch.matmul(X, w) + b

[定义损失函数]

def squared_loss(y_hat, y):  #@save
    """均方损失。"""
    return (y_hat - y.reshape(y_hat.shape))**2 / 2

(定义优化算法)

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降。"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

2 训练

现在我们已经准备好了模型训练所有需要的要素，可以实现主要的[训练过程]部分了。 理解这段代码至关重要，因为在整个深度学习的职业生涯中，你会一遍又一遍地看到几乎相同的训练过程。 在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。 计算完损失后，我们开始反向传播，存储每个参数的梯度。最后，我们调用优化算法 sgd 来更新模型参数。

概括一下，我们将执行以下循环：

• 初始化参数
• 重复，直到完成
  • 计算梯度 $\mathbf{g} \leftarrow \partial{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$
  • 更新参数 $(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$

在每个迭代周期（epoch）中，我们使用 data_iter 函数遍历整个数据集，并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。设置超参数很棘手，需要通过反复试验进行调整。 我们现在忽略这些细节，以后会在 :numref:chap_optimization 中详细介绍。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
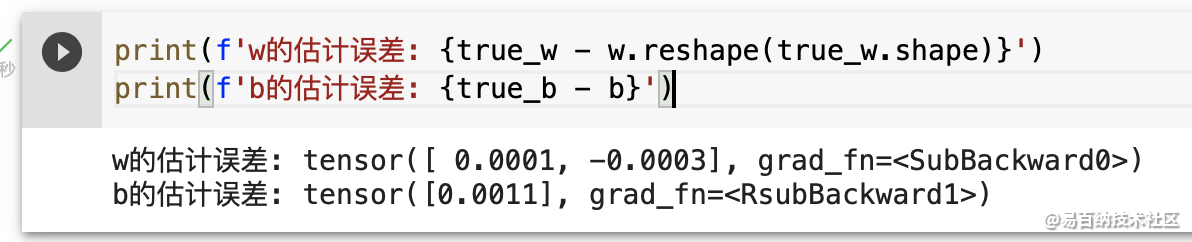
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

3 关于with

with是python中上下文管理器，简单理解，当要进行固定的进入，返回操作时，可以将对应需要的操作，放在with所需要的语句中。比如文件的写入（需要打开关闭文件）等。

以下为一个文件写入使用with的例子。

        with open (filename,'w') as sh:    
            sh.write("#!/bin/bash\n")
            sh.write("#$ -N "+'IC'+altas+str(patientNumber)+altas+'\n')
            sh.write("#$ -o "+pathSh+altas+'log.log\n') 
            sh.write("#$ -e "+pathSh+altas+'err.log\n') 
            sh.write('source ~/.bashrc\n')          
            sh.write('. "/home/kjsun/anaconda3/etc/profile.d/conda.sh"\n')
            sh.write('conda activate python27\n')
            sh.write('echo "to python"\n')
            sh.write('echo "finish"\n')
            sh.close()

with后部分，可以将with后的语句运行，将其返回结果给到as后的变量（sh），之后的代码块对close进行操作。

4 关于with torch.no_grad():

在使用pytorch时，并不是所有的操作都需要进行计算图的生成（计算过程的构建，以便梯度反向传播等操作）。而对于tensor的计算操作，默认是要进行计算图的构建的，在这种情况下，可以使用 with torch.no_grad():，强制之后的内容不进行计算图构建。

以下分别为使用和不使用的情况： 在这一过程中只使用张量和自动微分，不需要定义层或复杂的优化器

5 简介实现

5.1 定义模型

在 PyTorch 中，全连接层在 Linear 类中定义。值得注意的是，我们将两个参数传递到 nn.Linear 中。第一个指定输入特征形状，即 2，第二个指定输出特征形状，输出特征形状为单个标量，因此为 1。

# `nn` 是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

5.2 初始化模型参数

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

5.3 定义损失函数

loss = nn.MSELoss()

5.4 定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

5.5 训练

在每个迭代周期里，我们将完整遍历一次数据集（train_data），不停地从中获取一个小批量的输入和相应的标签。对于每一个小批量，我们会进行以下步骤:

通过调用 net(X) 生成预测并计算损失 l（正向传播）。 通过进行反向传播来计算梯度。 通过调用优化器来更新模型参数。 为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)#通过调用 net(X) 生成预测并计算损失 l（正向传播）
        trainer.zero_grad()#梯度清0
        l.backward()#通过进行反向传播来计算梯度。
        trainer.step()#通过调用优化器来更新模型参数。
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')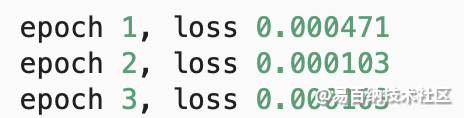

我们可以使用 PyTorch 的高级 API更简洁地实现模型。 在 PyTorch 中，data 模块提供了数据处理工具，nn 模块定义了大量的神经网络层和常见损失函数。 我们可以通过_ 结尾的方法将参数替换，从而初始化参数。

6 Pytorch完成模型常用API

在前一部分，我们自己实现了通过torch的相关方法完成反向传播和参数更新，在pytorch中预设了一些更加灵活简单的对象，让我们来构造模型、定义损失，优化损失等

那么接下来，我们一起来了解一下其中常用的API

6.1 nn.Module

nn.Modul 是torch.nn提供的一个类，是pytorch中我们自定义网络的一个基类，在这个类中定义了很多有用的方法，让我们在继承这个类定义网络的时候非常简单 用前面的y = wx+b的模型举例如下：

from torch import nn
class Lr(nn.Module):
    def __init__(self):
        super(Lr, self).__init__()  #继承父类init的参数
        self.linear = nn.Linear(1, 1) 

    def forward(self, x):
        out = self.linear(x)
        return out

nn.Linear为torch预定义好的线性模型，也被称为全链接层，传入的参数为输入的数量，输出的数量(in_features, out_features),是不算(batch_size的列数) nn.Module定义了call方法，实现的就是调用forward方法，即Lr的实例，能够直接被传入参数调用，实际上调用的是forward方法并传入参数

# 实例化模型
model = Lr()
# 传入数据，计算结果
predict = model(x)

6.2 优化器类

优化器(optimizer)，可以理解为torch为我们封装的用来进行更新参数的方法，比如常见的随机梯度下降(stochastic gradient descent,SGD)

优化器类都是由torch.optim提供的，例如

torch.optim.SGD(参数，学习率) torch.optim.Adam(参数，学习率) 注意：

参数可以使用model.parameters()来获取，获取模型中所有requires_grad=True的参数 优化类的使用方法 实例化 所有参数的梯度，将其值置为0 反向传播计算梯度 更新参数值 示例如下：

optimizer = optim.SGD(model.parameters(), lr=1e-3) #1. 实例化
optimizer.zero_grad() #2. 梯度置为0
loss.backward() #3. 计算梯度
optimizer.step()  #4. 更新参数的值

6.3 损失函数

前面的例子是一个回归问题，torch中也预测了很多损失函数

均方误差:nn.MSELoss(),常用于回归问题 交叉熵损失：nn.CrossEntropyLoss()，常用于分类问题 使用方法

model = Lr() #1. 实例化模型
criterion = nn.MSELoss() #2. 实例化损失函数
optimizer = optim.SGD(model.parameters(), lr=1e-3) #3. 实例化优化器类
for i in range(100):
    y_predict = model(x_true) #4. 向前计算预测值
    loss = criterion(y_true,y_predict) #5. 调用损失函数传入真实值和预测值，得到损失结果
    optimizer.zero_grad() #5. 当前循环参数梯度置为0
    loss.backward() #6. 计算梯度
    optimizer.step()  #7. 更新参数的值

6.4 Adam

Adam（Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法,能够达到防止梯度的摆幅多大，同时还能够加开收敛速度

torch中的api为：torch.optim.Adam()