【深度学习】强化学习Q-Learning和DQN的应用(迷宫)

【深度学习】强化学习Q-Learning和DQN的应用(迷宫)

文章目录
1 Q-Learning
2 例子
3 用 network 解决
4 DQN机器人走迷宫代码
    4.1 基础搜索算法介绍（广度优先搜索算法）
    4.2 DQN

1 Q-Learning

我们做事情都会有一个自己的行为准则, 比如小时候爸妈常说”不写完作业就不准看电视”. 所以我们在 写作业的这种状态下, 好的行为就是继续写作业, 直到写完它, 我们还可以得到奖励, 不好的行为 就是没写完就跑去看电视了, 被爸妈发现, 后果很严重. 小时候这种事情做多了, 也就变成我们不可磨灭的记忆. 这和我们要提到的 Q learning 有什么关系呢? 原来 Q learning 也是一个决策过程, 和小时候的这种情况差不多. 我们举例说明.

假设现在我们处于写作业的状态而且我们以前并没有尝试过写作业时看电视, 所以现在我们有两种选择 , 1, 继续写作业, 2, 跑去看电视. 因为以前没有被罚过, 所以我选看电视, 然后现在的状态变成了看电视, 我又选了 继续看电视, 接着我还是看电视, 最后爸妈回家, 发现我没写完作业就去看电视了, 狠狠地惩罚了我一次, 我也深刻地记下了这一次经历, 并在我的脑海中将 “没写完作业就看电视” 这种行为更改为负面行为, 我们在看看 Q learning 根据很多这样的经历是如何来决策的吧.

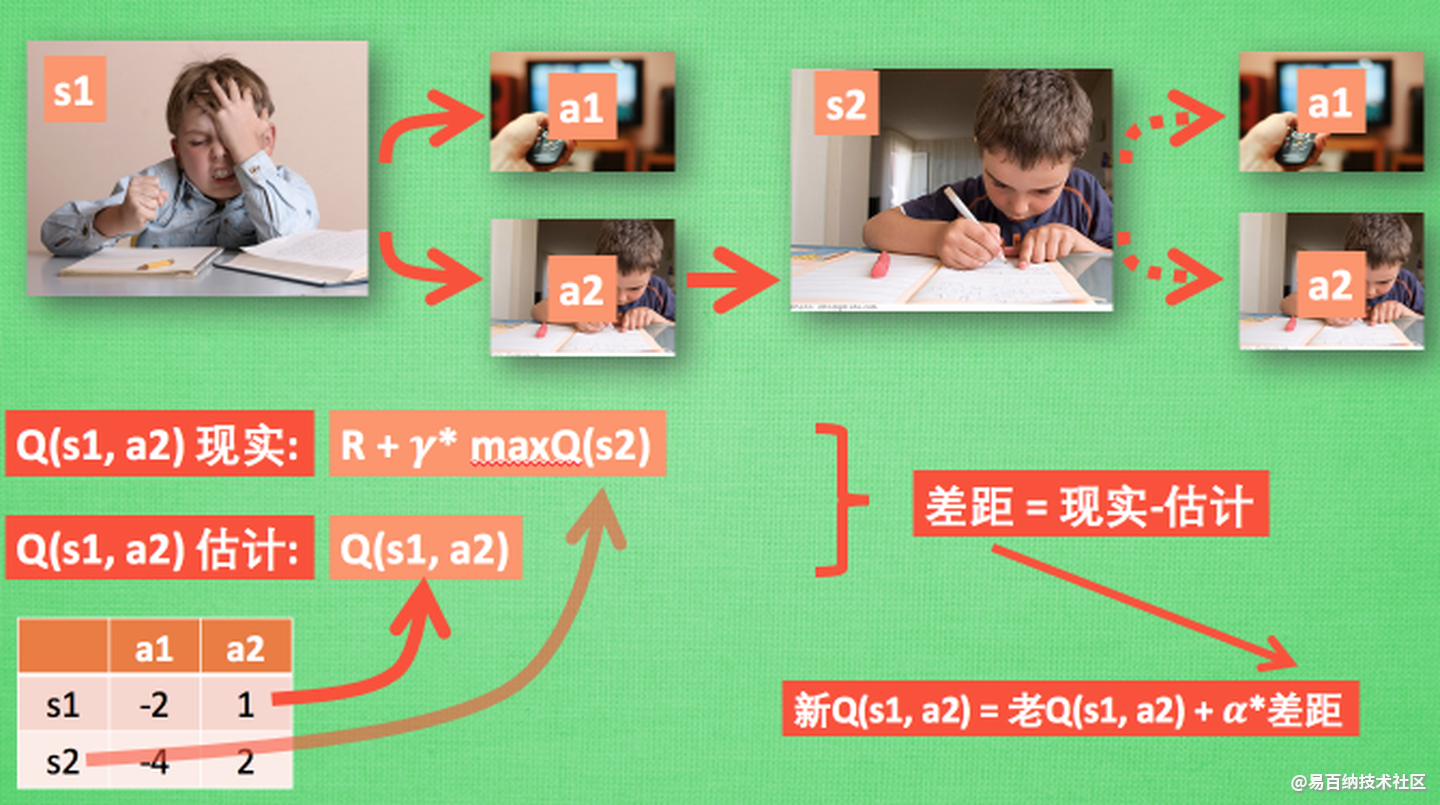
Q learning 的迷人之处就是 在 Q(s1, a2) 现实 中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧. 最后我们来说说这套算法中一些参数的意义. Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数. gamma 是对未来 reward 的衰减值. 我们可以这样想象.

2 例子

下面举一个例子加深以下了解。
以下是一个迷宫， s 表示起始点，e表示终点， t表示陷阱。规则：每走一步，reward 减 1, 若进入陷阱， reward 减100, 若到达终点, reward 加 100.

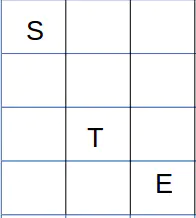
用 Q-table 解决
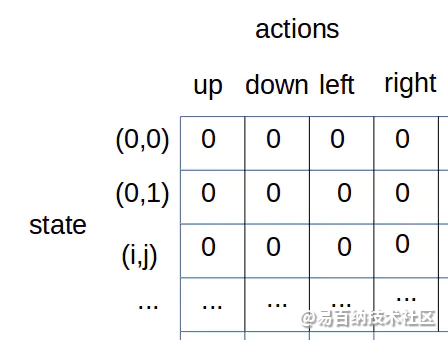
Q-table 的关键就是要建立一张映射表，这张表是 状态-动作 到 Q值的映射。如根据上面的问题，我们建立如下表格：

3 用 network 解决

假设我们的状态空间特别大，在这种情况下如果还坚持用 Q-table 来计算Q(s,a)的话，那么最终的Q-table对特别大，甚至计算机无法存储。为了解决这个问题，我们引入带参数的神经网络去近似Q(s,a)函数。

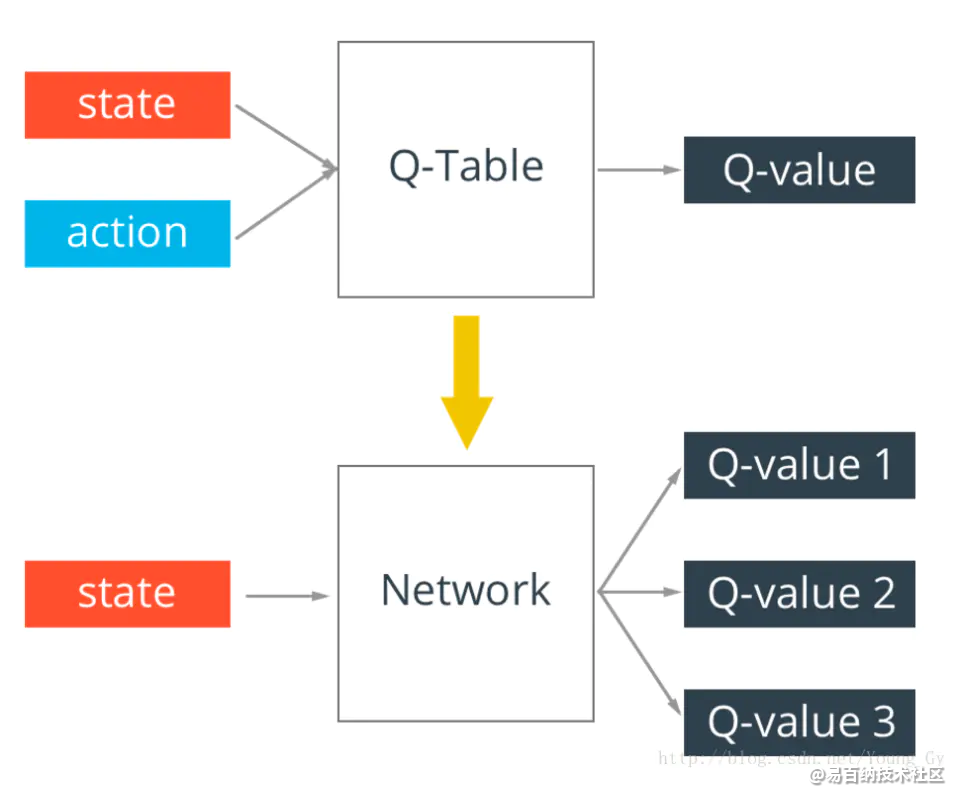
把原来的 Q-table 替换成 神经网络后，其算法并没有太大的变化。需要注意的是， 网络的Loss 函数是

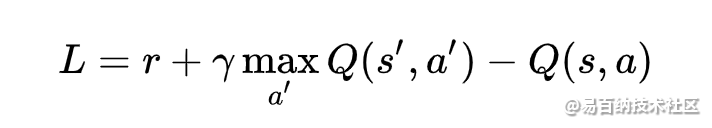
4 DQN机器人走迷宫代码

4.1 基础搜索算法介绍（广度优先搜索算法）

对于迷宫游戏，常见的三种的搜索算法有广度优先搜索、深度优先搜索和最佳优先搜索（A*)。

在下面的代码示例中，将实现广度优先搜索算法；主要通过建立一颗搜索树并进行层次遍历实现。

每个节点表示为以 Class SearchTree 实例化的对象，类属性有：当前节点位置、到达当前节点的动作、当前节点的父节点、当前节点的子节点；
valid_actions(): 用以获取机器人可以行走的位置（即不能穿墙）；
expand(): 对于未拓展的子节点进行拓展；
backpropagation(): 回溯搜索路径。
算法具体步骤
首先以机器人起始位置建立根节点，并入队；接下来不断重复以下步骤直到判定条件:

将队首节点的位置标记已访问；判断队首是否为目标位置(出口)， 是 则终止循环并记录回溯路径
判断队首节点是否为叶子节点，是 则拓展该叶子节点
如果队首节点有子节点，则将每个子节点插到队尾
将队首节点出队

def my_search(maze):
    """
    对迷宫进行广度优先搜索
    :param maze: 待搜索的maze对象
    """
    start = maze.sense_robot()
    root = SearchTree(loc=start)
    stack = [root]  
    h, w, _ = maze.maze_data.shape
    is_visit_m = np.zeros((h, w), dtype=np.int)  
    path = []  
    while True:
        current_node = stack[0]
        is_visit_m[current_node.loc] = 1  
        if current_node.loc == maze.destination:  
            path = back_propagation(current_node)
            break

        if current_node.is_leaf():
            expand(maze, is_visit_m, current_node)

        #入栈
        for child in current_node.children:
            stack.append(child)

        # 出栈
        stack.pop(0)

    return path

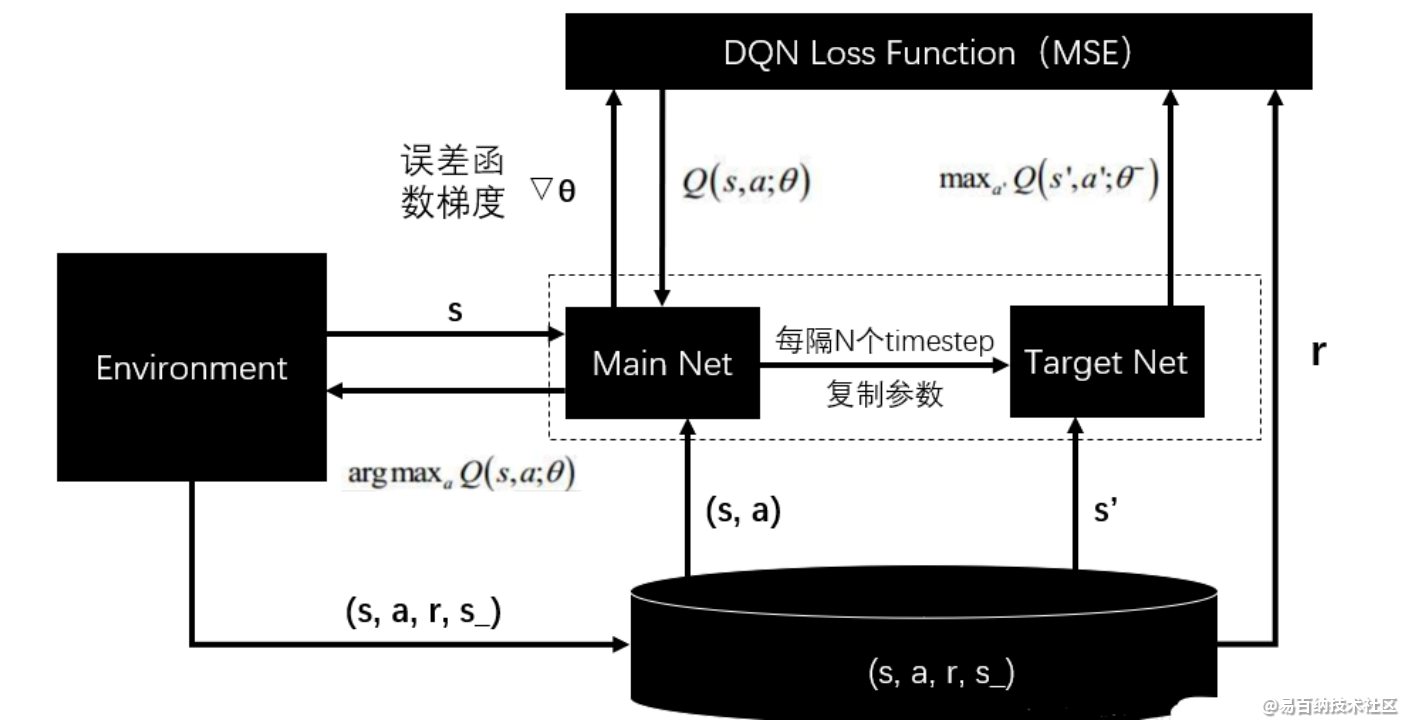
4.2 DQN

强化学习是一个反复迭代的过程，每一次迭代要解决两个问题：给定一个策略求值函数，和根据值函数来更新策略。而 DQN 算法使用神经网络来近似值函数.

    def train_update(self):
        state = self.sense_state()
        action = self._choose_action(state)
        reward = self.maze.move_robot(action)
        next_state = self.sense_state()
        is_terminal = 1 if next_state == self.maze.destination or next_state == state else 0

        self.memory.add(state, self.valid_action.index(action), reward, next_state, is_terminal)

        """--间隔一段时间更新target network权重--"""
        if self.step % self.EveryUpdate == 0:
            self._learn(batch=32)

        """---update the step and epsilon---"""
        self.step += 1
        self.epsilon = max(0.01, self.epsilon * 0.995)

        return action, reward

    def test_update(self):
        state = np.array(self.sense_state(), dtype=np.int16)
        state = torch.from_numpy(state).float().to(self.device)

        self.eval_model.eval()
        with torch.no_grad():
            q_value = self.eval_model(state).cpu().data.numpy()

        action = self.valid_action[np.argmin(q_value).item()]
        reward = self.maze.move_robot(action)
        return action, reward

简单的两层全连接神经网络决策动作

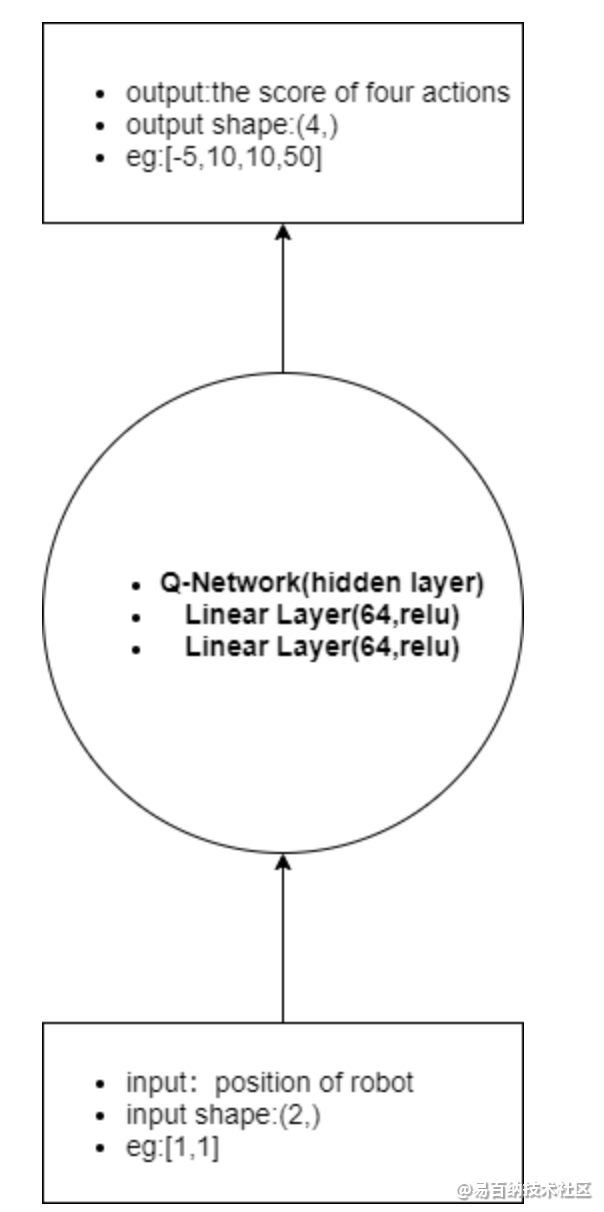
该神经网络的输入：机器人当前的位置坐标，输出：执行四个动作（up、right、down、left）的评估分数