【机器学习】通俗的元胞自动机算法解析和应用

【机器学习】通俗的元胞自动机算法解析和应用

文章目录
1 元胞自动机的定义
2 元胞自动机的组成
3 元胞自动机的特征
4 Python实现元胞自动机（生命游戏）
5 总结
6 Github（华盛顿州大黄峰分布预测和分类）

1 元胞自动机的定义

元胞自动机（Cellular Automata，简称CA）是一种应用比较广泛的模型理论，由冯·诺依曼创始，经数学家Conway、物理学家Wolfram等人的贡献后迅速发展。在物理学定义上，元胞自动机指的是，定义在一个由具有离散、有限状态的元胞组成的元胞空间上，按照一定的局部规则，在离散的时间维度上演化的动力学系统。在数学定义上，从不同的角度有着基于集合论的定义和拓扑学的定义，简单起见，在此不做阐述。
元胞自动机(cellular automata，CA) 是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。

2 元胞自动机的组成

元胞：又称细胞、单元或者基元，是元胞自动机最基本的组成部分。元胞分布在离散的欧几里得空间位置上，每个时刻有着离散的状态，如{0,1}等。

元胞空间：元胞所分布在欧几里得空间上的网格点的集合。最常见的为二维元胞空间，通常可按三角形、四边形和六边形三种网格排列。

邻居：元胞自动机的演化规则是局部的，对于指定元胞的状态进行更新时只需要知道其临近元胞的状态。某一元胞状态更新时要搜索的空间域叫做该元胞的邻居。

邻居的划分：在四方网格划分下的二维元胞自动机的邻居通常有以下几种形式：

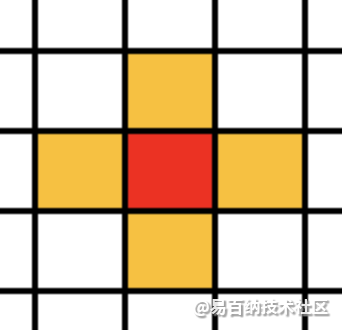
Von Neuman型

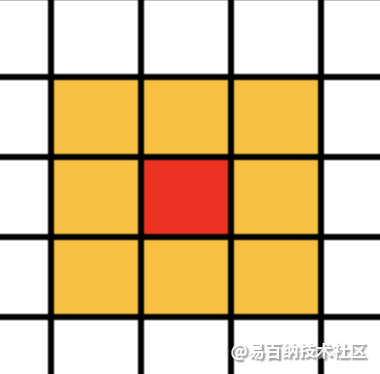
Moore型

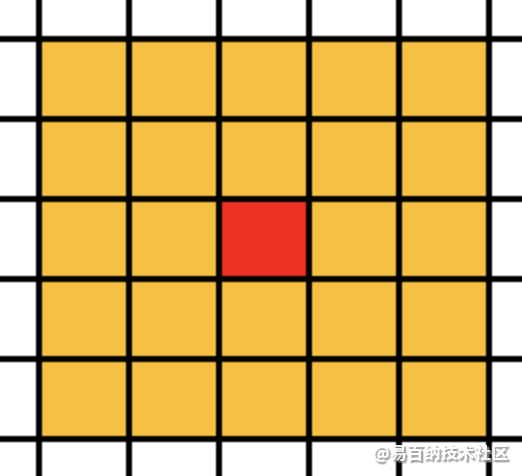
expend Moore型
边界条件：实际模拟元胞自动机的演化时不可能处理无限网络，系统必须是有边界的。处理边界格点时，可以为边界的信息进行编码，由此选择不同的演化规则。另一种方法是在边界处扩展，以满足边界有与内部类似的邻居。

周期型边界：周期型是指相对边界连接起来的元胞空间。这种空间与无限空间最为接近，进行理论探讨时，常以此类空间作为实验进行模拟。

固定边界：所有边界外元胞均取某一固定常量。

绝热边界：边界外元胞的状态始终和边界元胞的状态保持一致。

演化规则：根据元胞当前状态及其邻居状态确定下一时刻该元胞状态的动力学函数。

3 元胞自动机的特征

标准的元胞自动机具有以下几个特征：

（1）同质性、齐性：同质性反映在元胞空间内的每个元胞都服从相同的规则；齐性指的是元胞的分布方式相同，大小形状相同，空间分布整齐。

（2）空间离散：元胞分布在按一定规则划分的离散的元胞空间上。

（3）时间离散：系统的演化是按等时间间隔分步进行的。t时刻的状态只对t+1时刻的状态产生影响。

（4）状态离散、有限：元胞自动机的状态参量只能取有限个离散值。

（5）同步计算（并行性）：元胞自动机的处理是同步进行的。

（6）时空局域性：每个元胞在t+1时刻的状态，取决于其邻居的元胞在t时刻的状态。

（7）维数高：动力系统中一般将变量的个数成为维数。任何完备元胞自动机的元胞空间是在空间上的无穷集，每个元胞的状态是这个动力学系统的变量，因此元胞自动机是一类无穷维动力系统。

4 Python实现元胞自动机（生命游戏）

康威生命游戏（英语：Conway’s Game of Life），又称康威生命棋，是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。

它最初于1970年10月在《科学美国人》杂志上马丁·葛登能的“数学游戏”专栏出现。

概述
生命游戏是一个零玩家游戏。它包括一个二维矩形世界，这个世界中的每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的或死了的细胞的数量。如果相邻方格活着的细胞数量过多，这个细胞会因为资源匮乏而在下一个时刻死去；相反，如果周围活细胞过少，这个细胞会因太孤单而死去。实际中，玩家可以设定周围活细胞的数目怎样时才适宜该细胞的生存。如果这个数目设定过高，世界中的大部分细胞会因为找不到太多的活的邻居而死去，直到整个世界都没有生命；如果这个数目设定过低，世界中又会被生命充满而没有什么变化。

import numpy as np
import random
import copy
import matplotlib.pyplot as plt

#设定元胞生长棋盘的大小
length = 100
width = 200

#根据棋盘的长宽创建矩阵
cell = np.zeros((length,width),int)
cell_temp = copy.deepcopy(cell)

#初始化矩阵为一个随机的0-1矩阵，1代表细胞生存，0代表细胞死亡
for i in range(0,length):
    for j in range(0,width):
        cell_temp[i][j] = random.randint(0,1)

#进行下一次生存状态的判断
# 当前细胞为存活状态时，当周围的存活细胞低于2个时（不包含2个），该细胞变成死亡状态。（模拟生命数量稀少）
# 当前细胞为存活状态时，当周围有2个或3个存活细胞时，该细胞保持原样。
# 当前细胞为存活状态时，当周围有超过3个存活细胞时，该细胞变成死亡状态。（模拟生命数量过多）
# 当前细胞为死亡状态时，当周围有3个存活细胞时，该细胞变成存活状态。（模拟繁殖）

#当所有细胞状态不变时结束
#可能存在棋盘一直周期性变化，此时如果需要结束可手动结束
while not(cell_temp==cell).all():
    #通过读取cell矩阵，不断判断每一个单元格是存活还是死亡，将判断结果保存在cell_temp中，最终再复制给cell矩阵
    cell = copy.deepcopy(cell_temp)
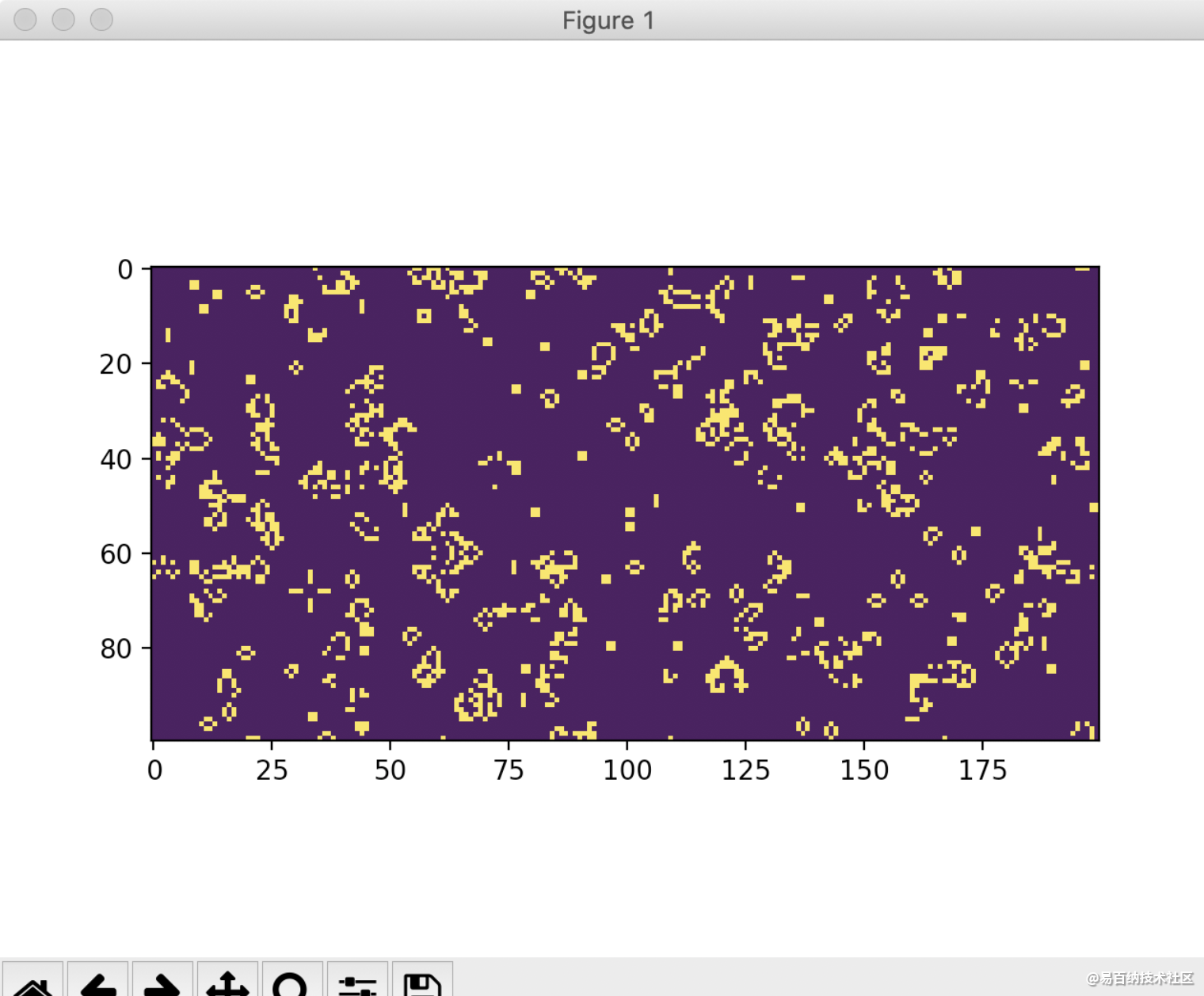
    #显示每一轮的图像
    plt.imshow(cell)
    plt.pause(0.2)
    #两重循环遍历整个矩阵，判断每个细胞下一个状态是生存还是死亡
    for i in range(0,length):
        for j in range(0,width):
            '''
            count保存一个细胞周围8个方格内有几个存活的细胞，注意这两将上下边界和左右边界连接起来进行判断，
            如对于8*8的棋盘,[0,0]与[0,7]和[7,0]在逻辑上相邻
            '''
            count = cell[(i-1)%length][j] + cell[(i+1)%length][j] + cell[i][(j-1)%width] + cell[i][(j+1)%width] + cell[(i+1)%length][(j+1)%width] + cell[(i-1)%length][(j+1)%width] + cell[(i+1)%length][(j-1)%width] + cell[(i-1)%length][(j-1)%width]
            #如果一个单元格是死亡，且周围是三个单元格则存活，否则保持死亡
            if(cell[i][j] == 0 and count != 3):
                continue
            if(cell[i][j] == 0 and count == 3):
                cell_temp[i][j] = 1
                continue
            #如果一个存活的单元格周围有2或3个单元格存活则该单元格继续存活，否则死亡
            if(count == 2 or count ==3):
                continue
            cell_temp[i][j] = 0

5 总结

简单说就是将一片区域（系统）分成很多个给定运动规则的单元格（可以说方形、六边形等），用单元格整体趋势来表示这片区域（系统）的演化趋势。散布在规则格网 (Lattice Grid)中的每一元胞(Cell)取有限的离散状态，遵循同样的作用规则，依据确定的局部规则作同步更新。大量元胞通过简单的相互作用而构成精态系统的演化。'它没有严格意义的函数限制,没有公式,行为复杂,是用一系列模型构造的规则构成的,所以只要满足这些规则的都可以使用这个模型.在实际应用过程中，有的元胞自动机模型对其中的某些特征进行了扩展，有的在规则设计中引入随机因素，如：森林火灾模型。 又如，在交通、通讯发达的今天， 研究流行病或计算机病毒的传播问题时， 我们还可以将空间背景换成复杂网络的结点，用网络邻接点作为邻居。这样的调整显然比仍旧使用二维欧氏空间、采用欧氏距离的模型更加符合实际情况。 在大型场所人群紧急疏散问题模拟研究中，可以考虑年龄、性别等因素，即元胞不是同质的，更加有利于使模拟系统接近真实系统。一般定义微观规则模拟交通堵塞和疏通的具体情况啊啥的，用matlab仿真可以得到具体问题的解，比如排队时间是多少，一个周期能排多少辆车，多长时间疏通都可以解。元胞自动机的方法比较新，大约90年代后通用，传统的有交通波和排队论.

6 Github（华盛顿州大黄峰分布预测和分类）

给个star哦！！

https://github.com/lixiang007666/Giant-Hornets-Intelligence-Algorithm