【深度学习】医学图像自动分割的评价指标讲解

文章目录
1 ROC-AUC
    1.1 混淆矩阵
    1.2 AUC计算
2 Precision和Recall
    2.1 概述
    2.2 MAP
    2.3 P-R曲线深入理解
3 语义分割的评价指标——IoU

1 ROC-AUC

1.1 混淆矩阵

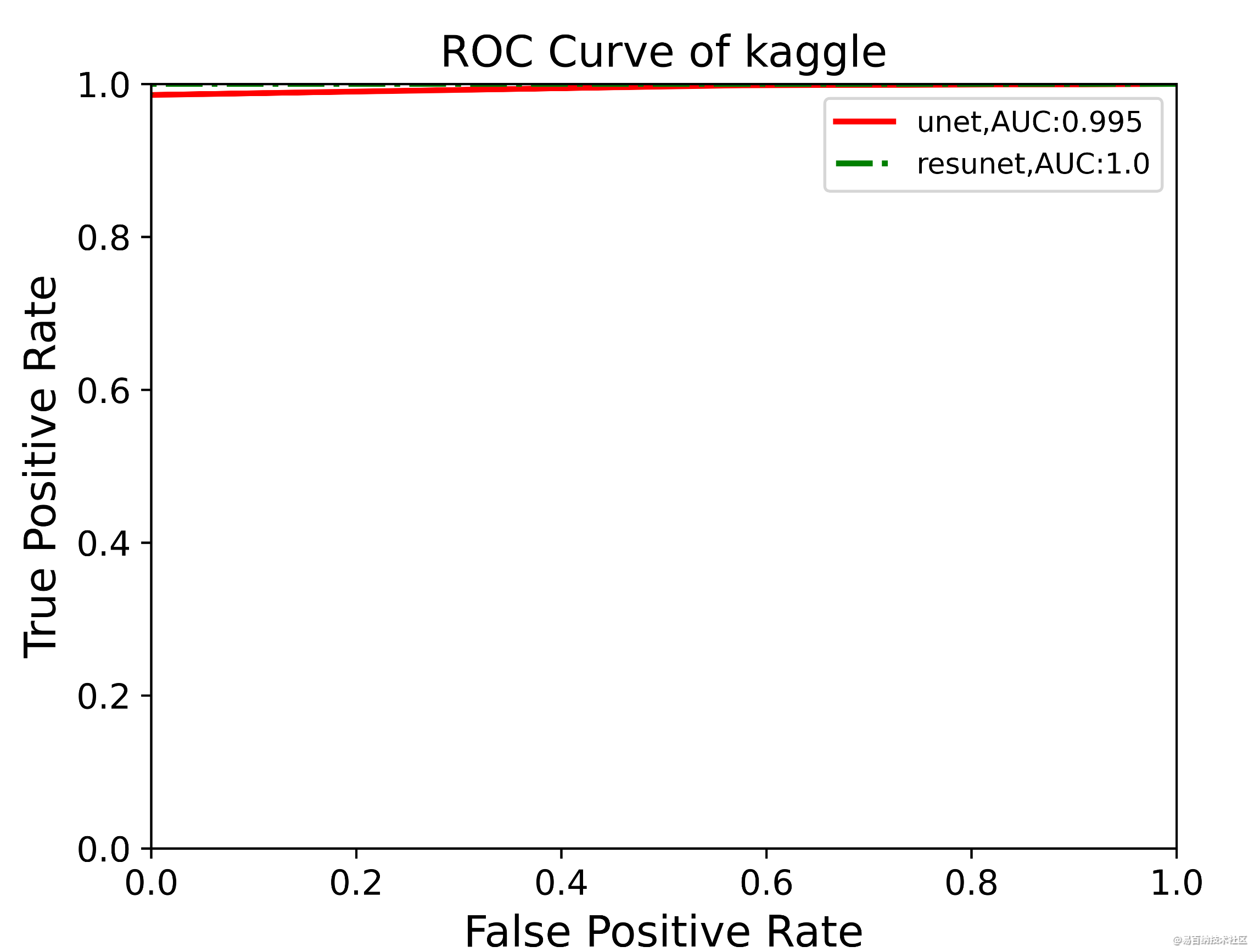
roc曲线：接收者操作特征(receiveroperating characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。

横轴：负正类率(false postive rate FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

纵轴：真正类率(true postive rate TPR)灵敏度，Sensitivity(正类覆盖率)

针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

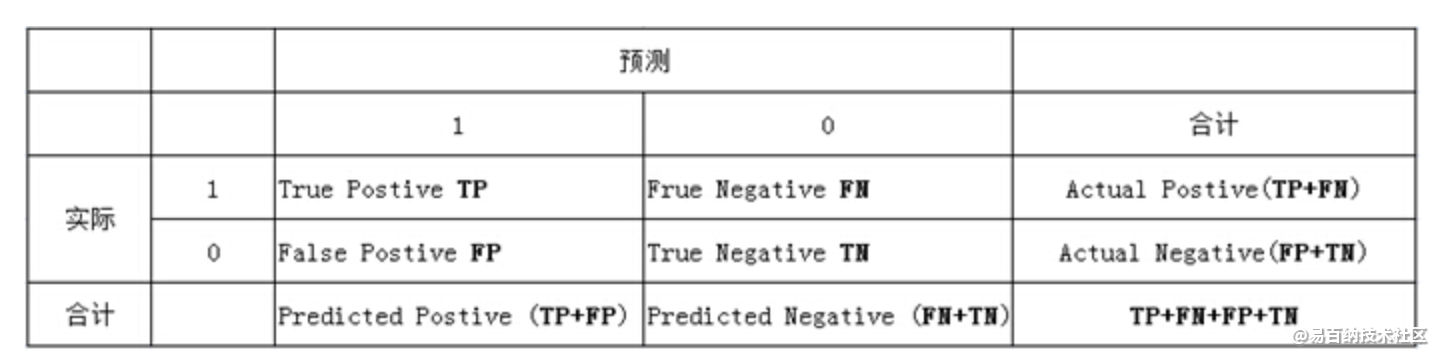
(1)若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)

(2)若一个实例是正类，但是被预测成为负类，即为假负类(False Negative FN)

(3)若一个实例是负类，但是被预测成为正类，即为假正类(False Postive FP)

(4)若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)
TP:正确的肯定数目

FN:漏报，没有找到正确匹配的数目

FP:误报，没有的匹配不正确

TN:正确拒绝的非匹配数目

列联表如下，1代表正类，0代表负类：

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity

(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity

(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。Specificity

从这个表格中可以引出一些其它的评价指标：

ACC：classification accuracy，描述分类器的分类准确率
计算公式为：ACC=(TP+TN)/(TP+FP+FN+TN)
BER：balanced error rate
计算公式为：BER=1/2*(FPR+FN/(FN+TP))
TPR：true positive rate，描述识别出的所有正例占所有正例的比例
计算公式为：TPR=TP/ (TP+ FN)
FPR：false positive rate，描述将负例识别为正例的情况占所有负例的比例
计算公式为：FPR= FP / (FP + TN)
TNR：true negative rate，描述识别出的负例占所有负例的比例
计算公式为：TNR= TN / (FP + TN)
PPV：Positive predictive value
计算公式为：PPV=TP / (TP + FP)
NPV：Negative predictive value
计算公式：NPV=TN / (FN + TN)
其中TPR即为敏感度（sensitivity），TNR即为特异度（specificity）。

1.2 AUC计算

最直观的，根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期 Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯 下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么 做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此 时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。

一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-Witney Test是等价的。这个等价关系的证明留在下篇帖子中给出。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。有了这个定义，我们就得到了另外一中计 算AUC的办法：得到这个概率。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。这 和上面的方法中，样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数（即n=M+N）

第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对score从大到小排序，然后令最大score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以M×N。即

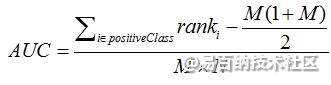
2 Precision和Recall

2.1 概述

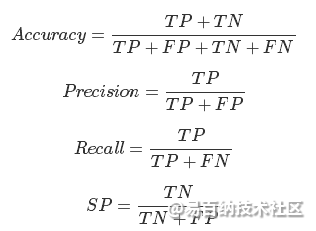
precision，准确率，表示预测结果中，预测为正样本的样本中，正确预测为正样本的概率；
recall，召回率，表示在原始样本的正样本中，最后被正确预测为正样本的概率；

在实际当中，我们往往希望得到的precision和recall都比较高，比如当FN和FP等于0的时候，他们的值都等于1。但是，它们往往在某种情况下是互斥的，比如这种情况，50个正样本，50个负样本，结果全部预测为正，那么它的precision为1而recall却为0.5.所以需要一种折衷的方式，因此就有了F1-score。

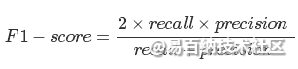
F1-score表示的是precision和recall的调和平均评估指标。

2.2 MAP

AP
我们可以通过一个简单的例子来说明平均准确率（AP）的计算。我们的数据集包含5个苹果。我们收集了模型关于苹果的所有预测结果并且根据置信水平对这些结果排序（从最高置信度到最低置信度）。第二列表明预测结果是否正确。如果跟真实值匹配并且IoU>=0.5表示正确。

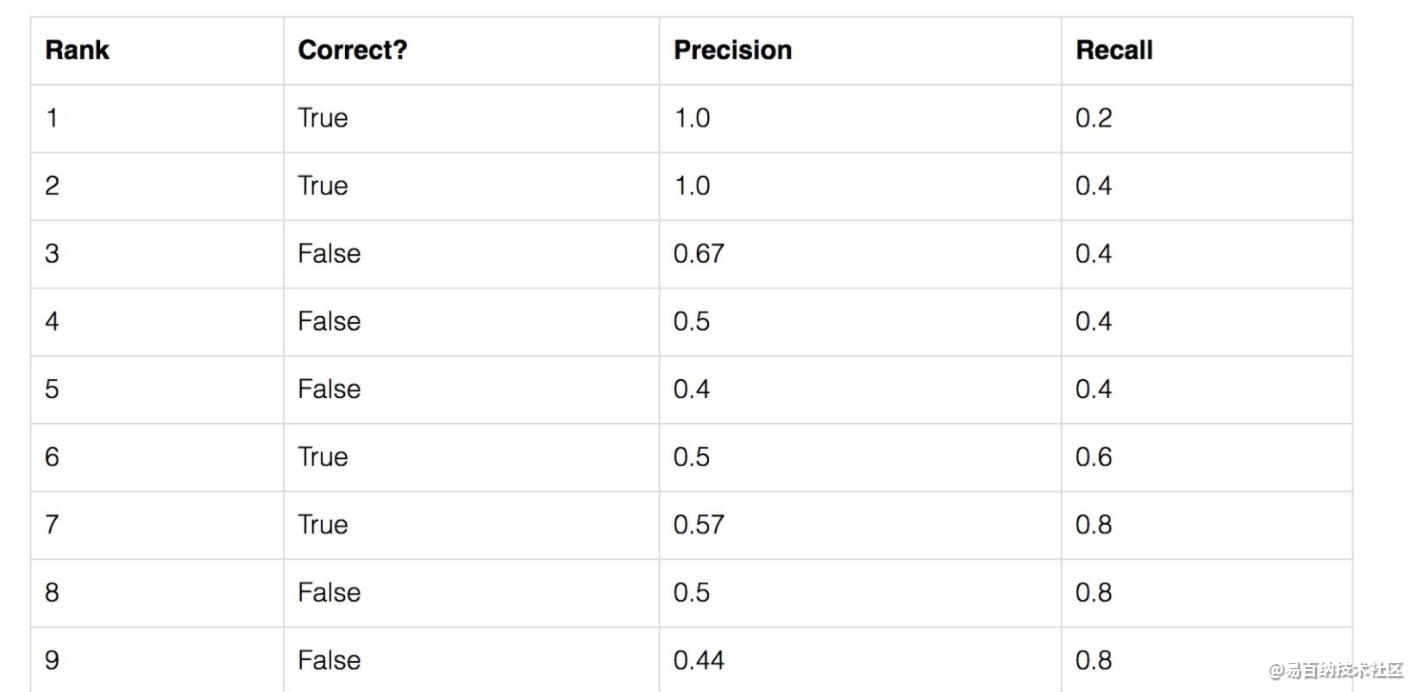
让我们计算Rank等于3这一行的精确率和召回率。
精确率是TP占预测结果的比例=2/3=0.67.
召回率是TP占所有正例的比例=2/5=0.4.
可以发现随着测试次数的增加，召回率在上升而精确率上下波动，精确率和召回率构成的曲线如下：

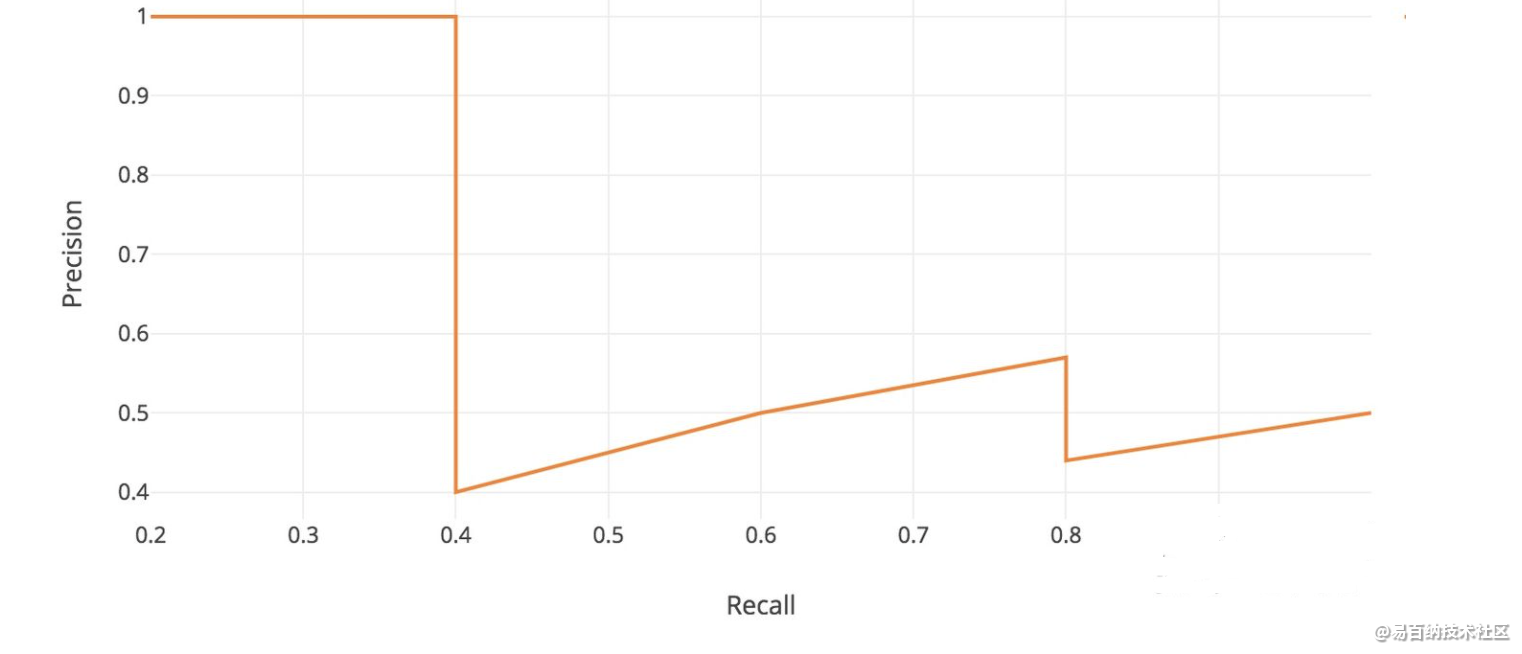
对于这个例子来说，可以轻易找到绿色曲线下面的区域并且除以11得到AP。下面是更加精确的定义。
从上面的例子可以看出，其实precision，recall都是选多少个样本k的函数，很容易想到，如果我总共有1000个样本，那么我就可以像这样计算1000对P-R，并且把他们画出来，这就是PR曲线：

这里有一个趋势，recall越高，precision越低。这是很合理的，因为假如说我把1000个全拿进来，那肯定正样本都包住了，recall=1，但是此时precision就很小了，因为我全部认为他们是正样本。recall=1时的precision的数值，等于正样本所占的比例。

所以AP，average precision，就是这个曲线下的面积，这里average，等于是对recall取平均。而mean average precision的mean，是对所有类别取平均（每一个类当做一次二分类任务）。现在的图像分类论文基本都是用mAP作为标准。

2.3 P-R曲线深入理解

精确率和召回率可以从混淆矩阵中计算而来，precision = TP/(TP + FP), recall = TP/(TP +FＮ)。那么P-R曲线是怎么来的呢？

算法对样本进行分类时，一般都会有置信度，即表示该样本是正样本的概率，比如99%的概率认为样本Ａ是正例，１％的概率认为样本B是正例。通过选择合适的阈值，比如50%，对样本进行划分，概率大于50%的就认为是正例，小于50%的就是负例。

通过置信度就可以对所有样本进行排序，再逐个样本的选择阈值，在该样本之前的都属于正例，该样本之后的都属于负例。每一个样本作为划分阈值时，都可以计算对应的precision和recall，那么就可以以此绘制曲线。那很多书上、博客上给出的P-R曲线，都长这样

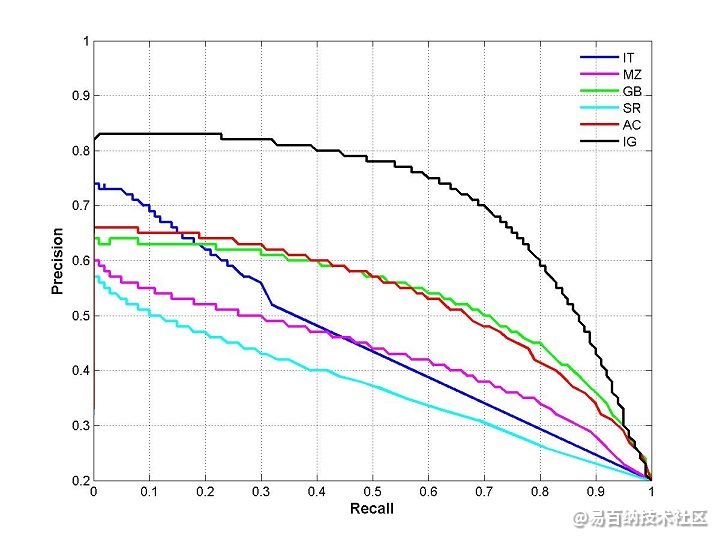
当然，这种曲线是有可能的。但是仔细琢磨就会发现一些规律和一些问题。

根据逐个样本作为阈值划分点的方法，可以推敲出，recall值是递增的（但并非严格递增），随着划分点左移，正例被判别为正例的越来越多，不会减少。而精确率precision并非递减，而是有可能振荡的，虽然正例被判为正例的变多，但负例被判为正例的也变多了，因此precision会振荡，但整体趋势是下降。

另外P-R曲线肯定会经过（0,0）点，比如讲所有的样本全部判为负例（或者是前面几个样本判决错了，将负例判决为了正例），则TP=0，那么P=R=0，因此会经过（0,0）点，但随着阈值点左移，precision初始很接近1，recall很接近0，因此有可能从（0,0）上升的线和坐标重合，不易区分。

曲线最终不会到（1,0）点。很多P-R曲线的终点看着都是（1,0）点，这可能是因为负例远远多于正例。

最后一个点表示所有的样本都被判为正例，因此FN=0，所以recall = TP/(TP + FN) = 1, 而FP = 所有的负例样本数，因此precision = TP/(TP+FP) = 正例的占所有样本的比例，故除非负例数很多，否则precision不会为0.

因此，较合理的P-R曲线应该是（曲线一开始被从（0，0）拉升到（0,1），并且前面的都预测对了，全是正例，因此precision一直是1,）

3 语义分割的评价指标——IoU

IoU指标就是大家常说的交并比，在语义分割中作为标准度量一直被人使用。交并比不仅仅在语义分割中使用，在目标检测等方向也是常用的指标之一。
计算公式为：


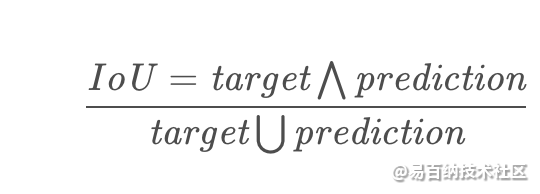
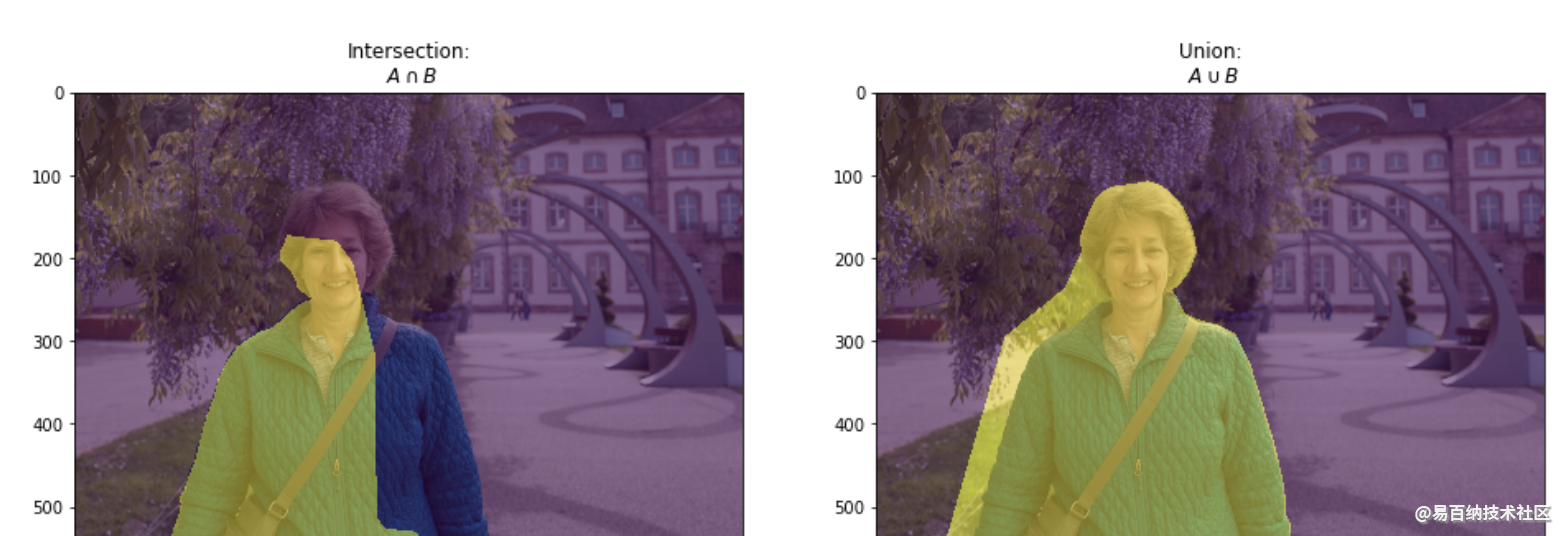
IoU一般都是基于类进行计算的，也有基于图片计算的。一定要看清数据集的评价标准，这里我吃过大亏，特意标注提醒。
基于类进行计算的IoU就是将每一类的IoU计算之后累加，再进行平均，得到的就是基于全局的评价，所以我们求的IoU其实是取了均值的IoU，也就是均交并比（mean IoU）

实现代码也很简单：intersection = np.logical_and(target, prediction) union = np.logical_or(target, prediction) iou_score = np.sum(intersection) / np.sum(union)
更具体的一些的如下所示：

import torch 
import pandas as pd  # For filelist reading
from torch.utils.data import Dataset
import myPytorchDatasetClass  # Custom dataset class, inherited from torch.utils.data.dataset

def iou(pred, target, n_classes = 37):
#n_classes ：the number of classes in your dataset
  ious = []
  pred = pred.view(-1)
  target = target.view(-1)

  # Ignore IoU for background class ("0")
  for cls in xrange(1, n_classes):  # This goes from 1:n_classes-1 -> class "0" is ignored
    pred_inds = pred == cls
    target_inds = target == cls
    intersection = (pred_inds[target_inds]).long().sum().data.cpu()[0]  # Cast to long to prevent overflows
    union = pred_inds.long().sum().data.cpu()[0] + target_inds.long().sum().data.cpu()[0] - intersection
    if union == 0:
      ious.append(float('nan'))  # If there is no ground truth, do not include in evaluation
    else:
      ious.append(float(intersection) / float(max(union, 1)))
  return np.array(ious)

def evaluate_performance(net):
    Dataloader for test data
    batch_size = 1  
    filelist_name_test = '/path/to/my/test/filelist.txt'
    data_root_test = '/path/to/my/data/'
    dset_test = myPytorchDatasetClass.CustomDataset(filelist_name_test, data_root_test)
    test_loader = torch.utils.data.DataLoader(dataset=dset_test,  
                                              batch_size=batch_size,
                                              shuffle=False,
                                              pin_memory=True)

    data_info = pd.read_csv(filelist_name_test, header=None)
    num_test_files = data_info.shape[0]  #reture data.info's hangshu that means dots in dataset 
    sample_size = num_test_files

    # Containers for results
    preds = torch.FloatTensor(sample_size, opt.imageSizeH, opt.imageSizeW)
    preds = Variable(seg,volatile=True)
    gts = torch.FloatTensor(sample_size, 1, opt.imageSizeH, opt.imageSizeW)
    gts = Variable(gts,volatile=True)

    dataiter = iter(test_loader) 
    for i in xrange(sample_size):
        images, labels, filename = dataiter.next()
        images = Variable(images).cuda()
        labels = Variable(labels)
        gts[i:i+batch_size, :, :, :] = labels
        outputs = net(images)
        outputs = outputs.permute(0, 2, 3, 4, 1).contiguous()
        val, pred = torch.max(outputs, 4)
        preds[i:i+batch_size, :, :, :] = pred.cpu()
    acc = iou(preds, gts)
    return acc