【机器学习】树回归和聚类算法解析和应用
【机器学习】树回归和聚类算法解析和应用

文章目录
1 树回归
2 CART ( Classification And Regression Tree) 分类回归树
3 K-means
3.1 合理选择 K 值
3.2 采用核函数
3.3 收敛证明
4 聚类应用1 树回归
树回归 概述
我们本章介绍 CART(Classification And Regression Trees, 分类回归树) 的树构建算法。该算法既可以用于分类还可以用于回归。
树回归 场景
当数据拥有众多特征并且特征之间关系十分复杂时,构建全局模型的想法就显得太难了,也略显笨拙。而且,实际生活中很多问题都是非线性的,不可能使用全局线性模型来拟合任何数据。
一种可行的方法是将数据集切分成很多份易建模的数据,然后利用我们的线性回归技术来建模。如果首次切分后仍然难以拟合线性模型就继续切分。在这种切分方式下,树回归和回归法就相当有用。
树回归 工作原理
1、找到数据集切分的最佳位置,函数 chooseBestSplit() 伪代码大致如下:
对每个特征:
对每个特征值:
将数据集切分成两份(小于该特征值的数据样本放在左子树,否则放在右子树)
计算切分的误差
如果当前误差小于当前最小误差,那么将当前切分设定为最佳切分并更新最小误差
返回最佳切分的特征和阈值
2、树构建算法,函数 createTree() 伪代码大致如下:
找到最佳的待切分特征:
如果该节点不能再分,将该节点存为叶节点
执行二元切分
在右子树调用 createTree() 方法
在左子树调用 createTree() 方法
1.4、树回归 开发流程
(1) 收集数据: 采用任意方法收集数据。
(2) 准备数据: 需要数值型数据,标称型数据应该映射成二值型数据。
(3) 分析数据: 绘出数据的二维可视化显示结果,以字典方式生成树。
(4) 训练算法: 大部分时间都花费在叶节点树模型的构建上。
(5) 测试算法: 使用测试数据上的R^2值来分析模型的效果。
(6) 使用算法: 使用训练处的树做预测,预测结果还可以用来做很多事情。
1.5、树回归 算法特点
优点: 可以对复杂和非线性的数据建模。
缺点: 结果不易理解。
适用数据类型: 数值型和标称型数据。

2 CART ( Classification And Regression Tree) 分类回归树
1、基尼指数:
在分类问题中,假设有KK 个类,样本点属于第kk 类的概率为PkPk ,则概率分布的基尼指数定义为:
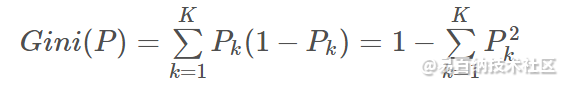
在CART 分类问题中,基尼指数作为特征选择的依据:选择基尼指数最小的特征及切分点做为最优特征和最优切分点。
2、在回归问题中,特征选择及最佳划分特征值的依据是:划分后样本的均方差之和最小!
二、算法分析:
CART 主要包括特征选择、回归树的生成、剪枝三部分
数据特征停止划分的条件:
1、当前数据集中的标签相同,返回当前的标签
2、划分前后的总方差差距很小,数据不划分,返回的属性为空,返回的最佳划分值为当前所有标签的均值。
3、划分后的左右两个数据集的样本数量较小,返回的属性为空,返回的最佳划分值为当前所有标签的均值。
若满足上述三个特征停止划分的条件,则返回的最佳特征为空,返回的最佳划分特征值会作为叶子结点。
注:CART是一棵二叉树。 在生成CART回归树过程中,一个特征可能会被使用不止一次,所以,不存在当前属性集为空的情况;
1、特征选择(依据:总方差最小)
输入:数据集、op = [m,n]
输出:最佳特征、最佳划分特征值
m表示剪枝前总方差与剪枝后总方差差值的最小值; n: 数据集划分为左右两个子数据集后,子数据集中的样本的最少数量;
1、判断数据集中所有的样本标签是否相同,是:返回当前标签;
2、遍历所有的样本特征,遍历每一个特征的特征值。计算出每一个特征值下的数据总方差,找出使总方差最小的特征、特征值
3、比较划分前和划分后的总方差大小;若划分后总方差减少较小,则返回的最佳特征为空,返回的最佳划分特征值会为当前数据集标签的平均值。
4、比较划分后的左右分支数据集样本中的数量,若某一分支数据集中样本少于指定数量op[1],则返回的最佳特征为空,
返回的最佳划分特征值会为当前数据集标签的平均值。
5、否则,返回使总方差最小的特征、特征值
二、回归树的生成函数 createTree
输入:数据集
输出:生成回归树
1、得到当前数据集的最佳划分特征、最佳划分特征值
2、若返回的最佳特征为空,则返回最佳划分特征值(作为叶子节点)
3、声明一个字典,用于保存当前的最佳划分特征、最佳划分特征值
4、执行二元切分;根据最佳划分特征、最佳划分特征值,将当前的数据划分为两部分
5、在左子树中调用createTree 函数, 在右子树调用createTree 函数。
6、返回树。
注:在生成的回归树模型中,划分特征、特征值、左节点、右节点均有相应的关键词对应。
三、(后)剪枝:(CART 树一定是二叉树,所以,如果发生剪枝,肯定是将两个叶子节点合并)
输入:树、测试集
输出:树
1、判断测试集是否为空,是:对树进行塌陷处理
2、判断树的左右分支是否为树结构,是:根据树当前的特征值、划分值将测试集分为Lset、Rset两个集合;
3、判断树的左分支是否是树结构:是:在该子集递归调用剪枝过程;
4、判断树的右分支是否是树结构:是:在该子集递归调用剪枝过程;
5、判断当前树结构的两个节点是否为叶子节点:
是:
a、根据当前树结构,测试集划分为Lset,Rset两部分;
b、计算没有合并时的总方差NoMergeError,即:测试集在Lset 和 Rset 的总方差之和;
c、合并后,取叶子节点值为原左右叶子结点的均值。求取测试集在该节点处的总方差MergeError,;
d、比较合并前后总方差的大小;若NoMergeError > MergeError,返回合并后的节点;否则,返回原来的树结构;
否:
返回树结构。
#-*- coding:utf-8 -*-
from numpy import *
import numpy as np
# 三大步骤:
'''
1、特征的选择:标准:总方差最小
2、回归树的生成:停止划分的标准
3、剪枝:
'''
# 导入数据集
def loadData(filaName):
dataSet = []
fr = open(filaName)
for line in fr.readlines():
curLine = line.strip().split('\t')
theLine = map(float, curLine) # map all elements to float()
dataSet.append(theLine)
return dataSet
# 特征选择:输入: 输出:最佳特征、最佳划分值
'''
1、选择标准
遍历所有的特征Fi:遍历每个特征的所有特征值Zi;找到Zi,划分后总的方差最小
停止划分的条件:
1、当前数据集中的标签相同,返回当前的标签
2、划分前后的总方差差距很小,数据不划分,返回的属性为空,返回的最佳划分值为当前所有标签的均值。
3、划分后的左右两个数据集的样本数量较小,返回的属性为空,返回的最佳划分值为当前所有标签的均值。
当划分的数据集满足上述条件之一,返回的最佳划分值作为叶子节点;
当划分后的数据集不满足上述要求时,找到最佳划分的属性,及最佳划分特征值
'''
# 计算总的方差
def GetAllVar(dataSet):
return var(dataSet[:,-1])*shape(dataSet)[0]
# 根据给定的特征、特征值划分数据集
def dataSplit(dataSet,feature,featNumber):
dataL = dataSet[nonzero(dataSet[:,feature] > featNumber)[0],:]
dataR = dataSet[nonzero(dataSet[:,feature] <= featNumber)[0],:]
return dataL,dataR
# 特征划分
def choseBestFeature(dataSet,op = [1,4]): # 三个停止条件可否当作是三个预剪枝操作
if len(set(dataSet[:,-1].T.tolist()[0]))==1: # 停止条件 1
regLeaf = mean(dataSet[:,-1])
return None, regLeaf # 返回标签的均值作为叶子节点
Serror = GetAllVar(dataSet)
BestFeature = -1; BestNumber = 0; lowError = inf
m,n = shape(dataSet) # m 个样本, n -1 个特征
for i in range(n-1): # 遍历每一个特征值
for j in set(dataSet[:,i].T.tolist()[0]):
dataL,dataR = dataSplit(dataSet,i,j)
if shape(dataR)[0]<op[1] or shape(dataL)[0]<op[1]: continue # 如果所给的划分后的数据集中样本数目甚少,则直接跳出
tempError = GetAllVar(dataL) + GetAllVar(dataR)
if tempError < lowError:
lowError = tempError; BestFeature = i; BestNumber = j
if Serror - lowError < op[0]: # 停止条件 2 如果所给的数据划分前后的差别不大,则停止划分(前剪枝操作)
return None, mean(dataSet[:,-1])
# dataL, dataR = dataSplit(dataSet, BestFeature, BestNumber)
# if shape(dataR)[0] < op[1] or shape(dataL)[0] < op[1]: # 停止条件 3
if BestFeature == -1 and BestNumber == 0:
return None, mean(dataSet[:, -1])
return BestFeature, BestNumber
# 决策树生成
def createTree(dataSet, op=[1, 4]):
bestFeat, bestNumber = choseBestFeature(dataSet, op)
if bestFeat==None: return bestNumber
regTree = {}
regTree['spInd'] = bestFeat
regTree['spVal'] = bestNumber
dataL,dataR = dataSplit(dataSet,bestFeat,bestNumber)
regTree['left'] = createTree(dataL,op)
regTree['right'] = createTree(dataR,op)
return regTree
# 后剪枝操作
# 用于判断所给的节点是否是叶子节点
def isTree(Tree):
return (type(Tree).__name__=='dict' )
# 计算两个叶子节点的均值
def getMean(Tree):
if isTree(Tree['left']): Tree['left'] = getMean(Tree['left'])
if isTree(Tree['right']):Tree['right'] = getMean(Tree['right'])
return (Tree['left']+ Tree['right'])/2.0
# 后剪枝
def pruneTree(Tree,testData):
if shape(testData)[0]==0: return getMean(Tree)
if isTree(Tree['left']) or isTree(Tree['right']):
dataL,dataR = dataSplit(testData,Tree['spInd'],Tree['spVal'])
if isTree(Tree['left']):
Tree['left'] = pruneTree(Tree['left'],dataL)
if isTree(Tree['right']):
Tree['right'] = pruneTree(Tree['right'],dataR)
if not isTree(Tree['left']) and not isTree(Tree['right']):
dataL,dataR = dataSplit(testData,Tree['spInd'],Tree['spVal'])
errorNoMerge = sum(power(dataL[:,-1] - Tree['left'],2)) + sum(power(dataR[:,-1] - Tree['right'],2))
leafMean = getMean(Tree)
errorMerge = sum(power(testData[:,-1] - leafMean,2))
if errorNoMerge > errorMerge:
print"the leaf merge"
return leafMean
else:
return Tree
else:
return Tree
# 预测
def forecastSample(Tree,testData):
if not isTree(Tree): return float(tree)
# print"选择的特征是:" ,Tree['spInd']
# print"测试数据的特征值是:" ,testData[Tree['spInd']]
if testData[0,Tree['spInd']]>Tree['spVal']:
if isTree(Tree['left']):
return forecastSample(Tree['left'],testData)
else:
return float(Tree['left'])
else:
if isTree(Tree['right']):
return forecastSample(Tree['right'],testData)
else:
return float(Tree['right'])
def TreeForecast(Tree,testData):
m = shape(testData)[0]
y_hat = mat(zeros((m,1)))
for i in range(m):
y_hat[i,0] = forecastSample(Tree,testData[i])
return y_hat
if __name__=="__main__":
print "hello world"
dataMat = loadData("ex2.txt")
dataMat = mat(dataMat)
op = [1, 6] # 参数1:剪枝前总方差与剪枝后总方差差值的最小值;参数2:将数据集划分为两个子数据集后,子数据集中的样本的最少数量;
theCreateTree = createTree(dataMat, op)
# 测试数据
dataMat2 = loadData("ex2.txt")
dataMat2 = mat(dataMat2)
# thePruneTree = pruneTree(theCreateTree, dataMat2)
#print"剪枝后的后树:\n",thePruneTree
y = dataMat2[:, -1]
y_hat = TreeForecast(theCreateTree,dataMat2)
# y_hat = TreeForecast(thePruneTree,dataMat2)
print corrcoef(y_hat,y,rowvar=0)[0,1] # 用预测值与真实值计算相关系数3 K-means
3.1 合理选择 K 值
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点,常见的选取 K 值的方法有:手肘法、Gap statistic 方法。
手肘法:
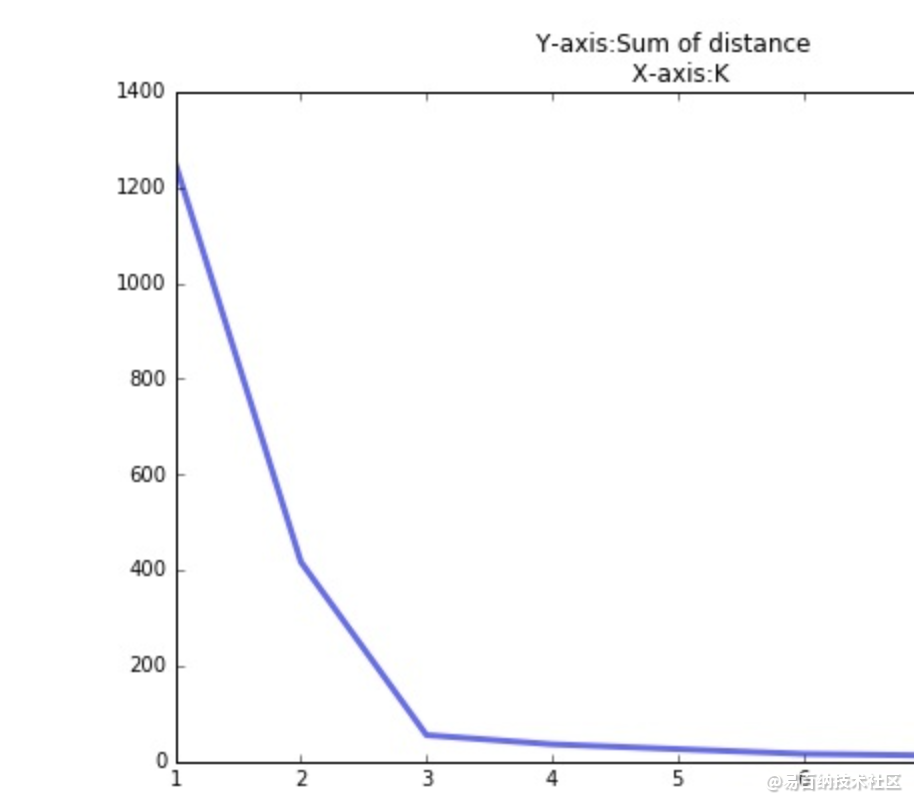
当 K < 3 时,曲线急速下降;当 K > 3 时,曲线趋于平稳,通过手肘法我们认为拐点 3 为 K 的最佳值。
手肘法的缺点在于需要人工看不够自动化,所以我们又有了 Gap statistic 方法,这个方法出自斯坦福大学的几个学者的论文:Estimating the number of clusters in a data set via the gap statistic
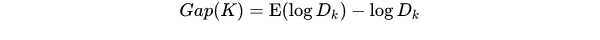
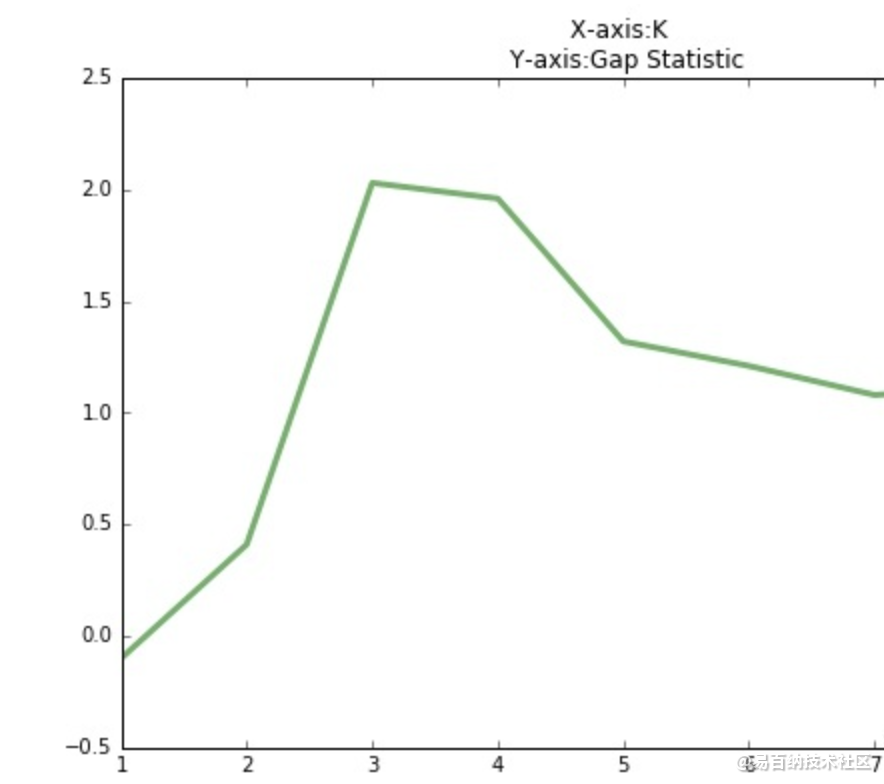
由图可见,当 K=3 时,Gap(K) 取值最大,所以最佳的簇数是 K=3。
Github 上一个项目叫 gap_statistic ,可以更方便的获取建议的类簇个数。
3.2 采用核函数
基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 K-means 算法,是核聚类方法的一种。核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
3.3 收敛证明
我们先来看一下 K-means 算法的步骤:先随机选择初始节点,然后计算每个样本所属类别,然后通过类别再跟新初始化节点。这个过程有没有想到之前介绍的 EM 算法 。
我们需要知道的是 K-means 聚类的迭代算法实际上是 EM 算法。EM 算法解决的是在概率模型中含有无法观测的隐含变量情况下的参数估计问题。在 K-means 中的隐变量是每个类别所属类别。K-means 算法迭代步骤中的 每次确认中心点以后重新进行标记 对应 EM 算法中的 E 步 求当前参数条件下的 Expectation 。而 根据标记重新求中心点 对应 EM 算法中的 M 步 求似然函数最大化时(损失函数最小时)对应的参数 。
4 聚类应用
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
iris = pd.read_csv(r'iris.csv')
# 设置聚为3类,n_clusters =3
X = iris.drop(labels = 'Species',axis = 1)
kmeans = KMeans(n_clusters =3 )
kmeans.fit(X)
X['cluster'] = kmeans.labels_
X.cluster.value_counts()
# 绘制花瓣长度与宽度的散点图
import seaborn as sns
centers = kmeans.cluster_centers_
print(centers)
sns.lmplot(x = 'Petal_Length',
y= 'Petal_Width',
hue = 'cluster',
markers = ['^','s','o'],
data = X,
fit_reg= False,
scatter_kws = {'alpha':0.8},
legend_out = False
)
plt.scatter(centers[:,2], centers[:,3], marker = '*',color = 'black', s =130) # 绘制簇中心点
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.show()
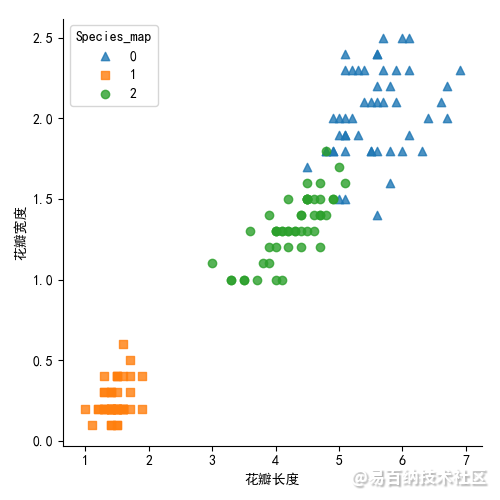
iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,"versicolor":2}) # 3种类型进行映射到0,1,2
sns.lmplot(x = 'Petal_Length',
y= 'Petal_Width',
hue = 'Species_map',
markers = ['^','s','o'],
data = iris,
fit_reg= False,
scatter_kws = {'alpha':0.8},
legend_out = False )
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.show()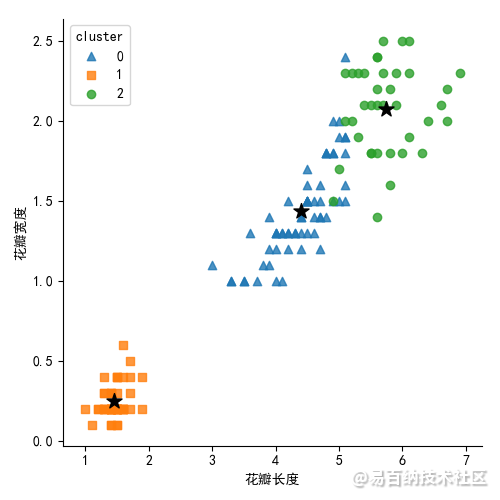
对簇中心做雷达图
import pygal
radar_chart = pygal.Radar(fill = True)
radar_chart.x_labels = ['花萼长度','花萼宽度', '花瓣长度','花瓣宽度']
# 雷达图区域绘制
radar_chart.add('C1',centers[0])
radar_chart.add('C2',centers[1])
radar_chart.add('C3',centers[2])
radar_chart.render_to_file('radar_chart.svg')
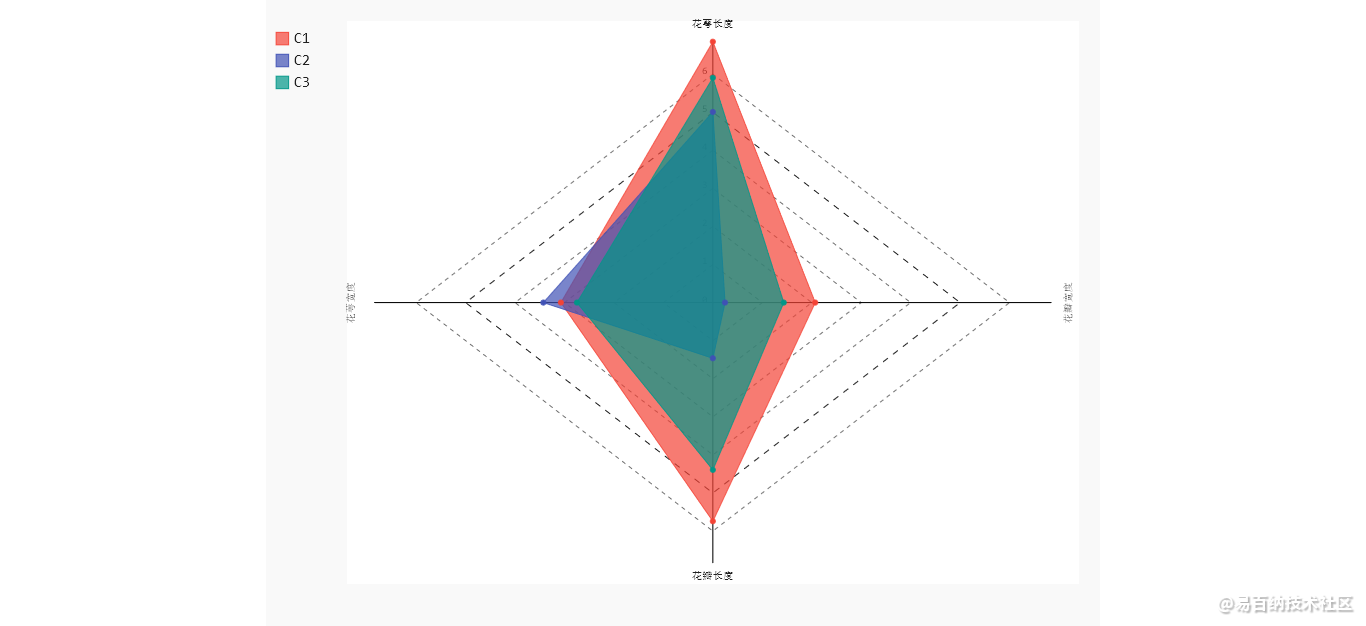
C1类型的花,花萼长和花瓣长都是最大的。C2类型的花,对应的3个指标值都比较小,C3类型的花,3个指标的平均值,恰好落在C1和C2之间。
NBA球员数据集聚类(未知k值)
数据集
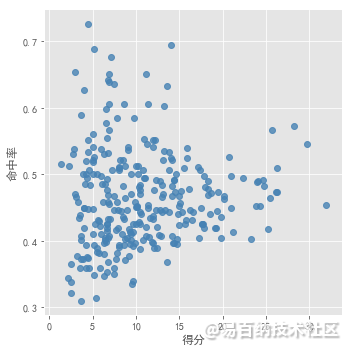
肉眼无法进行观察数据集适合分为几个簇。分别采用 以上确定k值的3种方法进行测试。
结果看出,k值在3、4斜率变化比较明显,在5以后斜率保持一定的水平。所以k取3,4,5均有可能。在比较其他方法。
轮廓系数法及Gap statistic法可视化效果如下:
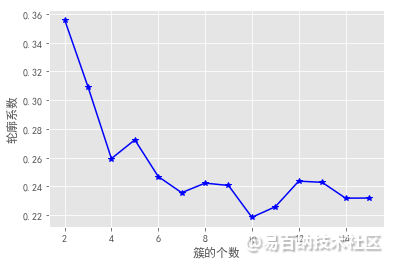
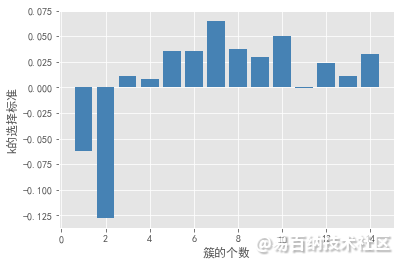
结合上图,轮廓系数在大于0的情况下,最大值对应的k值为2,统计量法首次出现正值的k值为3,综合考虑以上三种方法取k值为3,即将数据集分为3个簇最理想。
结果:
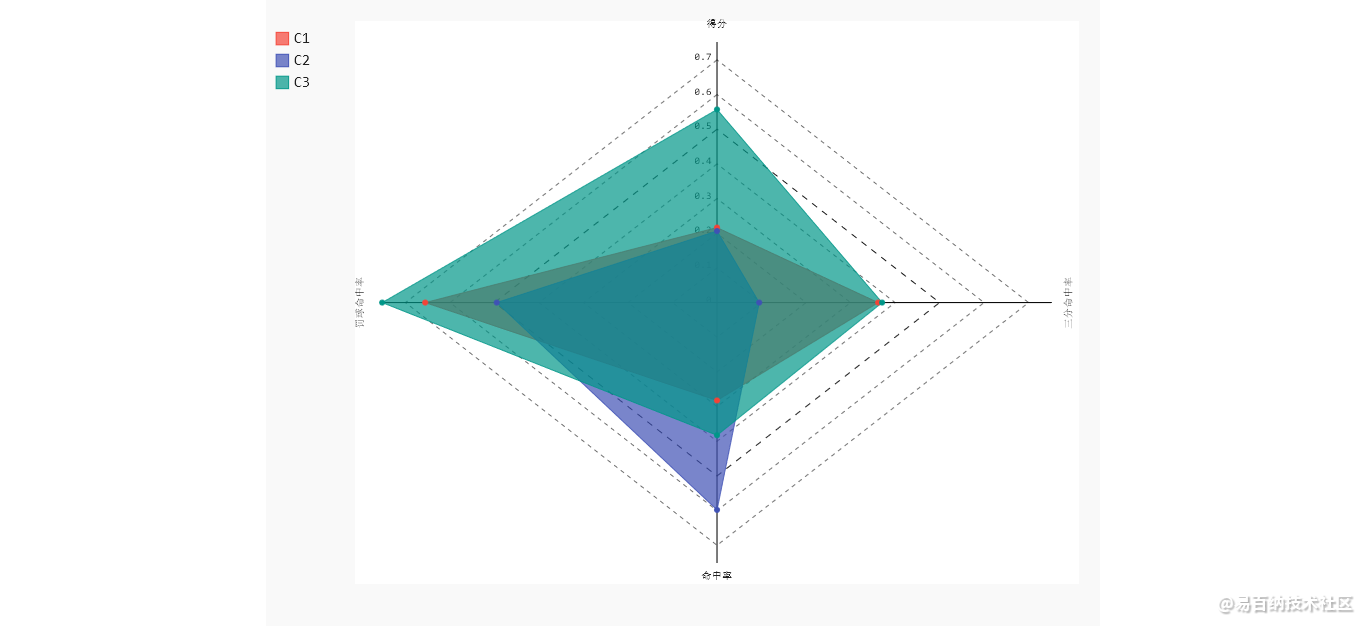
- 分享
- 举报
 暂无数据
暂无数据-
浏览量:4793次2021-06-28 14:10:22
-
浏览量:5330次2021-06-29 12:05:47
-
浏览量:999次2023-07-05 10:15:45
-
浏览量:919次2023-07-05 10:16:37
-
浏览量:12458次2021-07-07 16:10:35
-
浏览量:889次2023-07-24 15:23:06
-
浏览量:4337次2021-07-01 16:36:28
-
2023-01-13 11:35:13
-
浏览量:5370次2021-04-21 17:06:33
-
浏览量:902次2023-09-05 10:02:44
-
浏览量:5526次2021-08-05 09:20:49
-
浏览量:5362次2021-08-05 09:21:07
-
浏览量:4667次2021-06-30 11:34:00
-
浏览量:5246次2021-07-05 09:46:48
-
浏览量:3716次2019-09-18 22:22:32
-
浏览量:6011次2021-02-20 17:09:58
-
浏览量:5985次2021-04-20 15:43:03
-
浏览量:6167次2021-02-28 15:11:37
-
浏览量:6193次2021-04-14 16:24:29
-
广告/SPAM
-
恶意灌水
-
违规内容
-
文不对题
-
重复发帖
这把我C





 微信支付
微信支付举报类型
- 内容涉黄/赌/毒
- 内容侵权/抄袭
- 政治相关
- 涉嫌广告
- 侮辱谩骂
- 其他
详细说明


 微信扫码分享
微信扫码分享 QQ好友
QQ好友





