【机器学习】支持向量机和ensemble method的解析应用

【机器学习】支持向量机和ensemble method的解析应用

文章目录
1 SVM概述
2 项目案例: 手写数字识别的优化（有核函数）
3 随机森林
4 集成方法(Ensemble methods)
5 用Adaboost算法来预测森林火灾的发生
6 人脸识别（Adaboost）

1 SVM概述

支持向量机(Support Vector Machines, SVM): 是一种监督学习算法。

支持向量(Support Vector)就是离分隔超平面最近的那些点。
机(Machine)就是表示一种算法，而不是表示机器。
支持向量机 场景

要给左右两边的点进行分类
明显发现: 选择D会比B、C分隔的效果要好很多。

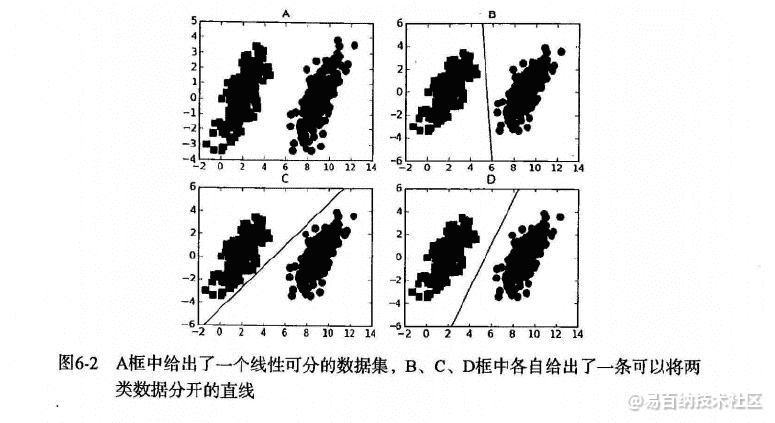
SVM 工作原理

对于上述的苹果和香蕉，我们想象为2种水果类型的zhadan。（保证距离最近的zhadan，距离它们最远）

寻找最大分类间距
转而通过拉格朗日函数求优化的问题
数据可以通过画一条直线就可以将它们完全分开，这组数据叫线性可分(linearly separable)数据，而这条分隔直线称为分隔超平面(separating hyperplane)。
如果数据集上升到1024维呢？那么需要1023维来分隔数据集，也就说需要N-1维的对象来分隔，这个对象叫做超平面(hyperlane)，也就是分类的决策边界。

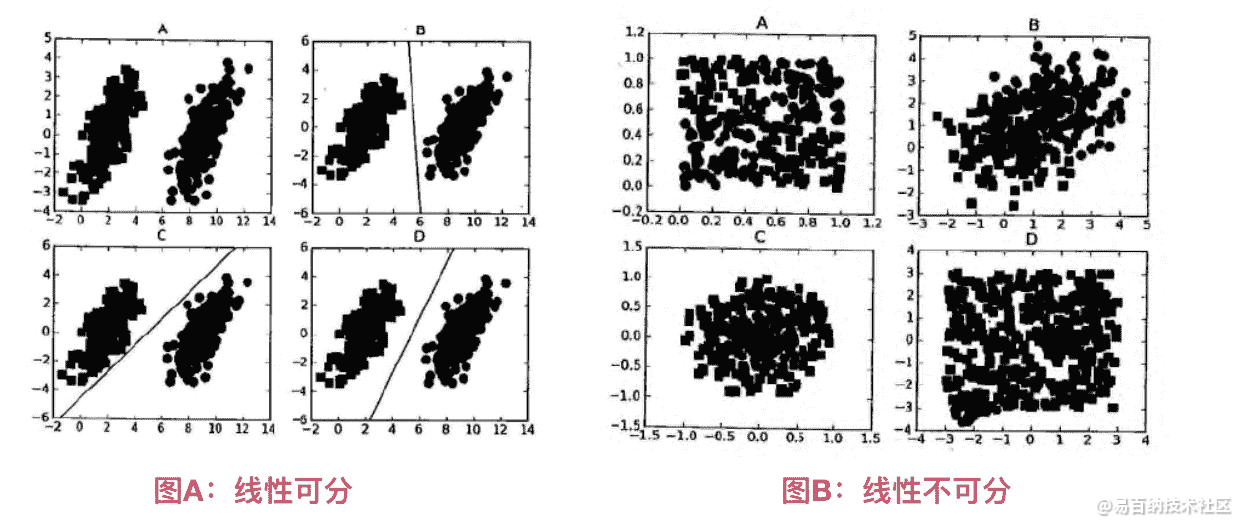
寻找最大间隔

为什么寻找最大间隔

摘录地址: http://slideplayer.com/slide/8610144 (第12条信息)
Support Vector Machines: Slide 12 Copyright © 2001, 2003, Andrew W. Moore Why Maximum Margin?

1.Intuitively this feels safest.
2.If we’ve made a small error in the location of the boundary (it’s been jolted in its perpendicular direction) this gives us least chance of causing a misclassification.
3.CV is easy since the model is immune to removal of any non-support-vector datapoints.
4.There’s some theory that this is a good thing.
5.Empirically it works very very well.

1. 直觉上是最安全的
2. 如果我们在边界的位置发生了一个小错误（它在垂直方向上被颠倒），这给我们最小的可能导致错误分类。
3. CV（cross validation 交叉验证）很容易，因为该模型对任何非支持向量数据点的去除是免疫的。
4. 有一些理论表明这是一件好东西。
5. 从经验角度上说它的效果非常非常好。
   怎么寻找最大间隔

点到超平面的距离
分隔超平面函数间距: $$y(x)=w^Tx+b$$
分类的结果: $$f(x)=sign(w^Tx+b)$$ (sign表示>0为1，<0为-1，=0为0)
点到超平面的几何间距: $$d(x)=(w^Tx+b)/||w||$$ （||w||表示w矩阵的二范数=> $$\sqrt{w^T*w}$$, 点到超平面的距离也是类似的）

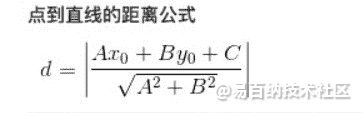
SVM 开发流程

收集数据: 可以使用任意方法。
准备数据: 需要数值型数据。
分析数据: 有助于可视化分隔超平面。
训练算法: SVM的大部分时间都源自训练，该过程主要实现两个参数的调优。
测试算法: 十分简单的计算过程就可以实现。
使用算法: 几乎所有分类问题都可以使用SVM，值得一提的是，SVM本身是一个二类分类器，对多类问题应用SVM需要对代码做一些修改。
SVM 算法特点

优点: 泛化（由具体的、个别的扩大为一般的，就是说: 模型训练完后的新样本）错误率低，计算开销不大，结果易理解。
缺点: 对参数调节和核函数的选择敏感，原始分类器不加修改仅适合于处理二分类问题。
使用数据类型: 数值型和标称型数据。

2 项目案例: 手写数字识别的优化（有核函数）

项目案例: 手写数字识别的优化（有核函数）

00000000000000001111000000000000
00000000000000011111111000000000
00000000000000011111111100000000
00000000000000011111111110000000
00000000000000011111111110000000
00000000000000111111111100000000
00000000000000111111111100000000
00000000000001111111111100000000
00000000000000111111111100000000
00000000000000111111111100000000
00000000000000111111111000000000
00000000000001111111111000000000
00000000000011111111111000000000
00000000000111111111110000000000
00000000001111111111111000000000
00000001111111111111111000000000
00000011111111111111110000000000
00000111111111111111110000000000
00000111111111111111110000000000
00000001111111111111110000000000
00000001111111011111110000000000
00000000111100011111110000000000
00000000000000011111110000000000
00000000000000011111100000000000
00000000000000111111110000000000
00000000000000011111110000000000
00000000000000011111110000000000
00000000000000011111111000000000
00000000000000011111111000000000
00000000000000011111111000000000
00000000000000000111111110000000
00000000000000000111111100000000

def kernelTrans(X, A, kTup):  # calc the kernel or transform data to a higher dimensional space
    """
    核转换函数
    Args:
        X     dataMatIn数据集
        A     dataMatIn数据集的第i行的数据
        kTup  核函数的信息

    Returns:

    """
    m, n = shape(X)
    K = mat(zeros((m, 1)))
    if kTup[0] == 'lin':
        # linear kernel:   m*n * n*1 = m*1
        K = X * A.T
    elif kTup[0] == 'rbf':
        for j in range(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T
        # 径向基函数的高斯版本
        K = exp(K / (-1 * kTup[1] ** 2))  # divide in NumPy is element-wise not matrix like Matlab
    else:
        raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
    return K

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    """
    完整SMO算法外循环，与smoSimple有些类似，但这里的循环退出条件更多一些
    Args:
        dataMatIn    数据集
        classLabels  类别标签
        C   松弛变量(常量值)，允许有些数据点可以处于分隔面的错误一侧。
            控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
            可以通过调节该参数达到不同的结果。
        toler   容错率
        maxIter 退出前最大的循环次数
        kTup    包含核函数信息的元组
    Returns:
        b       模型的常量值
        alphas  拉格朗日乘子
    """

    # 创建一个 optStruct 对象
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)
    iter = 0
    entireSet = True
    alphaPairsChanged = 0

    # 循环遍历: 循环maxIter次 并且 （alphaPairsChanged存在可以改变 or 所有行遍历一遍）
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0

        #  当entireSet=true or 非边界alpha对没有了；就开始寻找 alpha对，然后决定是否要进行else。
        if entireSet:
            # 在数据集上遍历所有可能的alpha
            for i in range(oS.m):
                # 是否存在alpha对，存在就+1
                alphaPairsChanged += innerL(i, oS)
                # print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1

        # 对已存在 alpha对，选出非边界的alpha值，进行优化。
        else:
            # 遍历所有的非边界alpha值，也就是不在边界0或C上的值。
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                # print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
            iter += 1

        # 如果找到alpha对，就优化非边界alpha值，否则，就重新进行寻找，如果寻找一遍 遍历所有的行还是没找到，就退出循环。
        if entireSet:
            entireSet = False  # toggle entire set loop
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b, oS.alphas

3 随机森林

构造随机森林的 4 个步骤

一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
按照步骤1~3建立大量的决策树，这样就构成了随机森林了

随机森林是由许多决策树组成的模型。这个模型不是简单地平均所有树（我们可以称之为“森林”）的预测，而是使用了两个关键概念，名字中的随机二字也是由此而来：

 ●  在构建树时对训练数据点进行随机抽样
 ●  分割节点时考虑特征的随机子集

随机抽样训练观测数据
在训练时，随机森林中的每棵树都会从数据点的随机样本中学习。样本被有放回的抽样，称为自助抽样法（bootstrapping），这意味着一些样本将在一棵树中被多次使用。背后的想法是在不同样本上训练每棵树，尽管每棵树相对于特定训练数据集可能具有高方差，但总体而言，整个森林将具有较低的方差，同时不以增加偏差为代价。

在测试时，通过平均每个决策树的预测来进行预测。这种在不同的自助抽样数据子集上训练单个学习器，然后对预测进行平均的过程称为bagging，是bootstrap aggregating的缩写。

4 集成方法(Ensemble methods)

1.1 什么是集成方法
简单来说，集成方法 就是组合多个模型，以获得更好效果。

1.2 两种集成方法
平均法(averaging methods)：也有人直接称之为“袋装法”，所有算法进行 相互独立 训练得到各自的模型，然后再进行投票选择最好的模型。如 随机森林(Forests of randomized trees) 与 袋装法(Bagging methods) 。
提升法(boosting methods)： 训练开始后，从第二个模型开始，每个模型是针对前一个模型进行加权叠加。如 自适应提升(Adaboost) 与 梯度树提升(Gradient Tree Boosting) 。
2 随机森林(Random Forests)
2.1 “森林”
在随机森林中，集合中的每棵树都是 从训练集中抽取的替换样本中构建的。大量的这样的树，即构成了所说的“森林”。

2.2 “随机”
在树的构造过程中分割每个节点时，可以从所有输入特征中找到最佳分割，也可以在1~max_features 范围中随机选取若干个特征进行分割节点操作。

2.3 作用
这两种随机性来源的目的是降低森林估计器的方差。事实上，单个决策树通常表现出高方差，并且倾向于过度拟合。森林中的注入随机性使得决策树具有一定程度的解耦预测误差。
通过取这些预测的平均值，一些错误可以抵消。随机森林通过组合不同的树来减少方差，有时以稍微增加偏差为代价。在实践中，方差的减少通常是显著的，因此产生了一个整体上更好的模型。

2.4 优点
对于很多种数据，它可以产生高准确度的分类器；
它可以处理大量的输入变数；
它可以在决定类别时，评估变数的重要性；
在建造森林时，它可以在内部对于一般化后的误差产生不偏差的估计；
它包含一个好方法可以估计遗失的资料，并且，如果有很大一部分的资料遗失，仍可以维持准确度；
它提供一个实验方法，可以去侦测variable interactions；
对于不平衡的分类资料集来说，它可以平衡误差；
它计算各例中的亲近度，对于数据挖掘、侦测离群点（outlier）和将资料视觉化非常有用；
使用上述。它可被延伸应用在未标记的资料上，这类资料通常是使用非监督式聚类。也可侦测偏离者和观看资料；
学习速度快。

5 用Adaboost算法来预测森林火灾的发生

数据来源：http://archive.ics.uci.edu/ml/machine-learning-databases/forest-fires/

1.问题与数据阐述
根据数据集，来预测森立火灾的发生与否。

数据类型：标称型和数值型

数据样本：

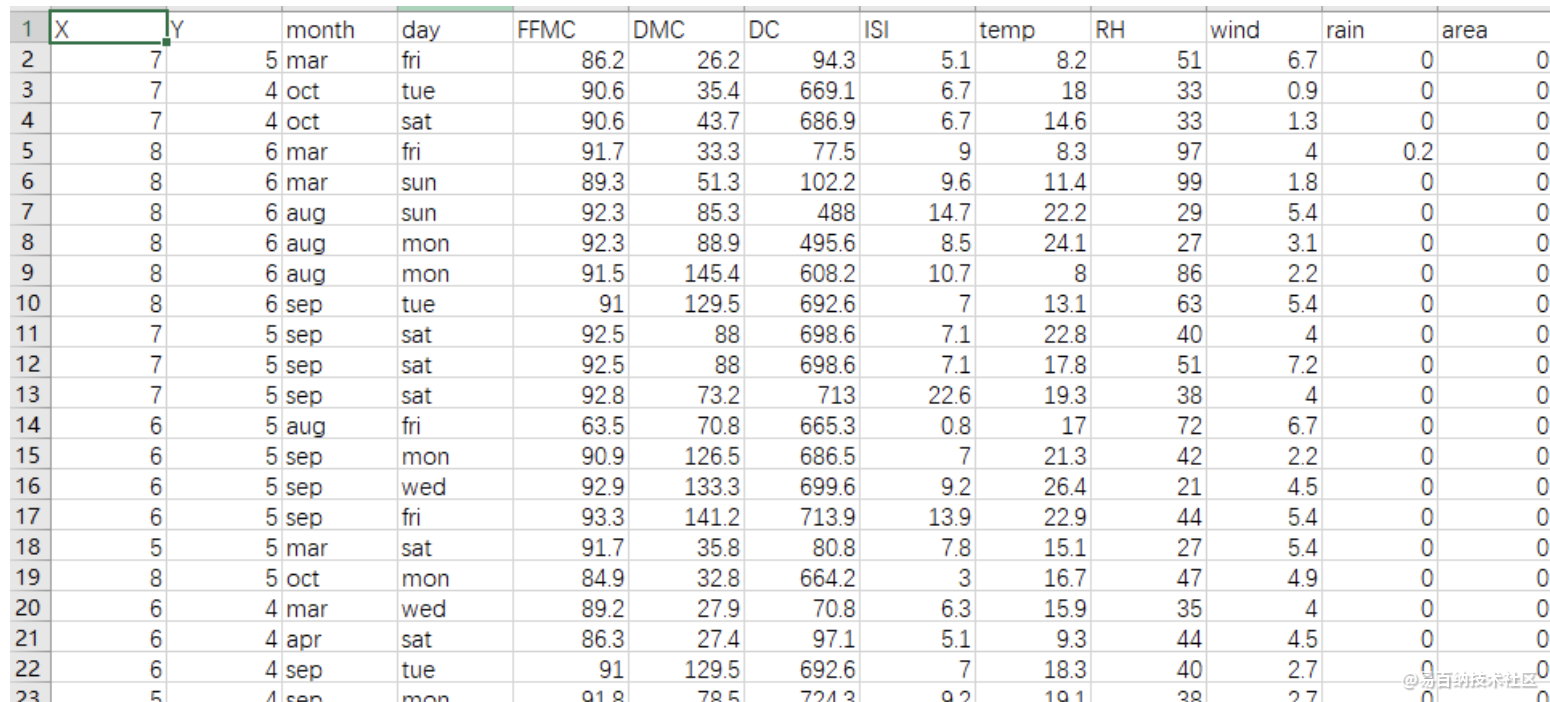
X:代表森林区域的横坐标，范围是1-9

Y:代表森林区域的纵坐标，范围是1-9

month:代表月份

day:代表一星期中的周几

FFMC:FWI系统中的一项数据（具体是啥我也不知道...应该是跟火灾密切相关的数据。），范围是18.7-96.2

DMC:FWI系统中的一项数据，范围是1.1-291.3

DC:FWI系统中的一项数据，范围是7.9-860.6

ISI:FWI系统中的一项数据，范围是0.0-56.1

temp:摄氏度，范围是2.2-33.3

RH:相对湿度，范围是15%-100%

wind:风速，单位：km/h，范围是0.4-9.4

rain:单位面积降水量，单位：mm/平方米，范围是0-6.4

area:森林火灾区域面积，单位：ha，范围是0-1090.84

2.数据预处理
数据集中每个样本特征并不是都影响到最后的分类结果，首先认为判断month与day这两项与火灾发生没有关联，将这2项特征排除。在审查数据集，发现rain这一项的值只有极少数样本不为0，可以判断这一项对分类也没有影响。

最关键的一点是，area的数据不是只有两种值（当然该数据集应该是用来判断火灾面积= =！，我这里为了使用Adaboost算法，只好改成分类问题），应该人为处理将area的值变成有且只有两种值。在这里，我们将area等于0的样本，area赋值为1，其余样本的area，赋值为-1。这样就能判断火灾是否发生。

数据集没有缺失项。

def plotROC(predStrengths, classLabels):
    import matplotlib.pyplot as plt
    cur = (1.0,1.0) #cursor
    ySum = 0.0 #variable to calculate AUC
    numPosClas = sum(array(classLabels)==1.0)
    yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
    sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
    fig = plt.figure()
    fig.clf()
    ax = plt.subplot(111)
    #loop through all the values, drawing a line segment at each point
    for index in sortedIndicies.tolist()[0]:
        if classLabels[index] == 1.0:
            delX = 0; delY = yStep;
        else:
            delX = xStep; delY = 0;
            ySum += cur[1]
        #draw line from cur to (cur[0]-delX,cur[1]-delY)
        ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
        cur = (cur[0]-delX,cur[1]-delY)
    ax.plot([0,1],[0,1],'b--')
    plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
    plt.title('ROC curve for AdaBoost forestfires')
    ax.axis([0,1,0,1])
    plt.show()
    print("the Area Under the Curve is: ",ySum*xStep)\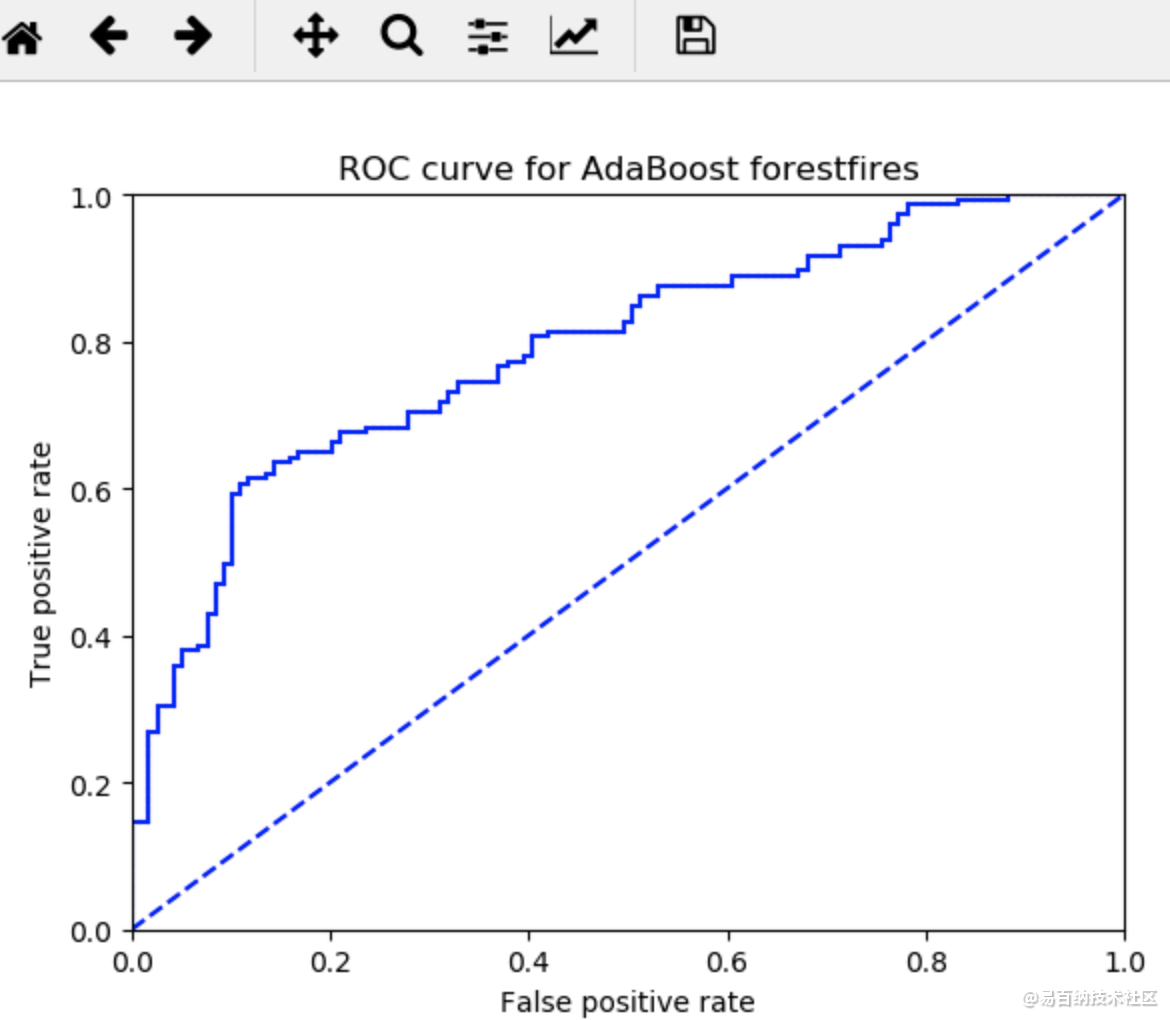

可以看出，预测的错误率很高，需要更改分类器数量。

6 人脸识别（Adaboost）

https://download.csdn.net/download/mark_jz/1050957?utm_medium=distribute.pc_relevant.none-task-download-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-download-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control