【机器学习】基于概率论的分类方法和Logistic回归

jm

文章目录
1 朴素贝叶斯
2 朴素贝叶斯图像像素分割实战——Nemo鱼图像分割（python代码+详细注释）
3 Logistic回归
4 梯度上升法
5 Logistic回归总结

1 朴素贝叶斯

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。本章首先介绍贝叶斯分类算法的基础——贝叶斯定理。最后，我们通过实例来讨论贝叶斯分类的中最简单的一种: 朴素贝叶斯分类。

贝叶斯理论

我们现在有一个数据集，它由两类数据组成，数据分布如下图所示:

我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别 1（图中用圆点表示的类别）的概率，用 p2(x,y) 表示数据点 (x,y) 属于类别 2（图中三角形表示的类别）的概率，那么对于一个新数据点 (x,y)，可以用下面的规则来判断它的类别:

如果 p1(x,y) > p2(x,y) ，那么类别为1
如果 p2(x,y) > p1(x,y) ，那么类别为2
也就是说，我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想，即选择具有最高概率的决策。
使用条件概率来分类

上面我们提到贝叶斯决策理论要求计算两个概率 p1(x, y) 和 p2(x, y):

如果 p1(x, y) > p2(x, y), 那么属于类别 1;
如果 p2(x, y) > p1(X, y), 那么属于类别 2.
这并不是贝叶斯决策理论的所有内容。使用 p1() 和 p2() 只是为了尽可能简化描述，而真正需要计算和比较的是 p(c1|x, y) 和 p(c2|x, y) .这些符号所代表的具体意义是: 给定某个由 x、y 表示的数据点，那么该数据点来自类别 c1 的概率是多少？数据点来自类别 c2 的概率又是多少？注意这些概率与概率 p(x, y|c1) 并不一样，不过可以使用贝叶斯准则来交换概率中条件与结果。具体地，应用贝叶斯准则得到

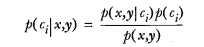
如果 P(c1|x, y) > P(c2|x, y), 那么属于类别 c1;
如果 P(c2|x, y) > P(c1|x, y), 那么属于类别 c2.
在文档分类中，整个文档（如一封电子邮件）是实例，而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词，并把每个词作为一个特征，而每个词的出现或者不出现作为该特征的值，这样得到的特征数目就会跟词汇表中的词的数目一样多。

我们假设特征之间 相互独立 。所谓 独立(independence) 指的是统计意义上的独立，即一个特征或者单词出现的可能性与它和其他单词相邻没有关系，比如说，“我们”中的“我”和“们”出现的概率与这两个字相邻没有任何关系。这个假设正是朴素贝叶斯分类器中 朴素(naive) 一词的含义。朴素贝叶斯分类器中的另一个假设是，每个特征同等重要。

Note: 朴素贝叶斯分类器通常有两种实现方式: 一种基于伯努利模型实现，一种基于多项式模型实现。这里采用前一种实现方式。该实现方式中并不考虑词在文档中出现的次数，只考虑出不出现，因此在这个意义上相当于假设词是等权重的。

朴素贝叶斯 场景

机器学习的一个重要应用就是文档的自动分类。

在文档分类中，整个文档（如一封电子邮件）是实例，而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词，并把每个词作为一个特征，而每个词的出现或者不出现作为该特征的值，这样得到的特征数目就会跟词汇表中的词的数目一样多。

朴素贝叶斯是上面介绍的贝叶斯分类器的一个扩展，是用于文档分类的常用算法。下面我们会进行一些朴素贝叶斯分类的实践项目。

朴素贝叶斯 原理

朴素贝叶斯 工作原理

提取所有文档中的词条并进行去重
获取文档的所有类别
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现在文档中-->增加该词条的计数值（for循环或者矩阵相加）
增加所有词条的计数值（此类别下词条总数）
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到的条件概率（P(词条|类别)）
返回该文档属于每个类别的条件概率（P(类别|文档的所有词条)）
朴素贝叶斯 开发流程

收集数据: 可以使用任何方法。
准备数据: 需要数值型或者布尔型数据。
分析数据: 有大量特征时，绘制特征作用不大，此时使用直方图效果更好。
训练算法: 计算不同的独立特征的条件概率。
测试算法: 计算错误率。
使用算法: 一个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器，不一定非要是文本。
朴素贝叶斯 算法特点

优点: 在数据较少的情况下仍然有效，可以处理多类别问题。
缺点: 对于输入数据的准备方式较为敏感。
适用数据类型: 标称型数据。

2 朴素贝叶斯图像像素分割实战——Nemo鱼图像分割（python代码+详细注释）

图像fish.bmp与掩膜mask.mat，掩膜点乘图像，即可获得待分割区域ROI。小鱼区域主要有两种类型的区域，以下就是要用朴素贝叶斯把这两个部分分出来——用不同的颜色表示不同区域。

训练数据sample.mat，它是一个二维的matlab数组，第一列为灰度值，第2-4列为RGB值，第五列为当前灰度值或者RGB值对应的类别标签（1，-1）。它蕴含着两种类型区域的灰度值或者RGB值的分布，根据它来估计两种类型区域的类概率密度函数的参数。

任务
  任务1：对训练数据用极大似然，估计出两类区域灰度值的概率密度函数，并用最小错误贝叶斯对fish.bmpROI灰度图像进行分割。
  任务2：对训练数据用极大似然，估计出两类区域RGB值的概率密度函数，并用最小错误贝叶斯对fish.bmpROI彩色图像进行分割。

理论与实现
  统计模型的训练过程就是类条件概率密度函数参数的估计过程。通过参数估计方法，从训练样本中估计出参数，便完成了训练。测试或者说应用过程就是用估计出的类概率密度函数和代表类别占比的先验概率进行统计决策或者分类的过程。最大似然是常用的参数估计方法，用在高斯混合模型（GMM）中。

极大似然估计
  假定我们面对的就是一个高斯混合模型（GMM），即每个类别训练样本的灰度值或者RGB值均服从正态分布，正态分布含有两个参数，均值方差或者均值协方差。

  我们知道，极大似然的目的是要找到最可能产生该样本序列的概率密度函数的参数。而在某概率密度函数参数下产生该样本序列的概率如式（1），即似然函数。

算法流程
  算法流程如下图所示，前半部分时统计模型的训练过程，即用最大似然（MLE）进行参数估计。测试过程，就是用决策的过程，图中为为Nemo鱼逐像素做灰度或者颜色决策或者分割的过程。PDF为scipy包中包含的正态分布PDF函数，只需给其参数和输入即可得到输出值。

 一维贝叶斯决策，计算一维输入时贝叶斯后验概率。

# 一维时，贝叶斯
# ------------------------------------------------------------------------------------#
# 数据为一维时(灰度图像)，用最大似然估计两个类别条件概率pdf的参数——标准差与均值
gray1_m = np.mean(gray1)
gray1_s = np.std(gray1)
gray2_m = np.mean(gray2)
gray2_s = np.std(gray2)
# print(gray1_s, gray2_s)

# 绘制最大似然估计出的类条件pdf
x = np.arange(0, 1, 1/1000)
gray1_pdf = norm.pdf(x, gray1_m, gray1_s)
gray2_pdf = norm.pdf(x, gray2_m, gray2_s)

plt.figure(0)
ax = plt.subplot(2, 1, 1)
ax.set_title('p(x|w)')

ax.plot(x, gray1_pdf, 'r', x, gray2_pdf, 'b')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
ax1 = plt.subplot(2, 1, 2)
ax1.plot(x, P_pre1*gray1_pdf, 'r', x, P_pre2*gray2_pdf, 'b')
ax1.set_title('p(w)*p(x|w)')
ax1.set_xlabel('x')
ax1.set_ylabel('f(x)')

# 用最大后验贝叶斯对灰度图像进行分割
gray_out = np.zeros_like(Gray_img)
for i in range(len(Gray_ROI)):
    for j in range(len(Gray_ROI[0])):
        if Gray_ROI[i][j] == 0:
            continue
        elif P_pre1*norm.pdf(Gray_ROI[i][j], gray1_m, gray1_s) > P_pre2*norm.pdf(Gray_ROI[i][j], gray2_m, gray2_s):   # 贝叶斯公式分子比较
            gray_out[i][j] = 100
        else:
            gray_out[i][j] = 255

# plt.imshow(RGB_ROI)
plt.figure(1)
bx = plt.subplot(1, 1, 1)
bx.set_title('gray ROI')
bx.imshow(Gray_ROI, cmap='gray')
plt.figure(2)
bx1 = plt.subplot(1, 1, 1)
bx1.set_title('gray segment result')
bx1.imshow(gray_out, cmap='gray')

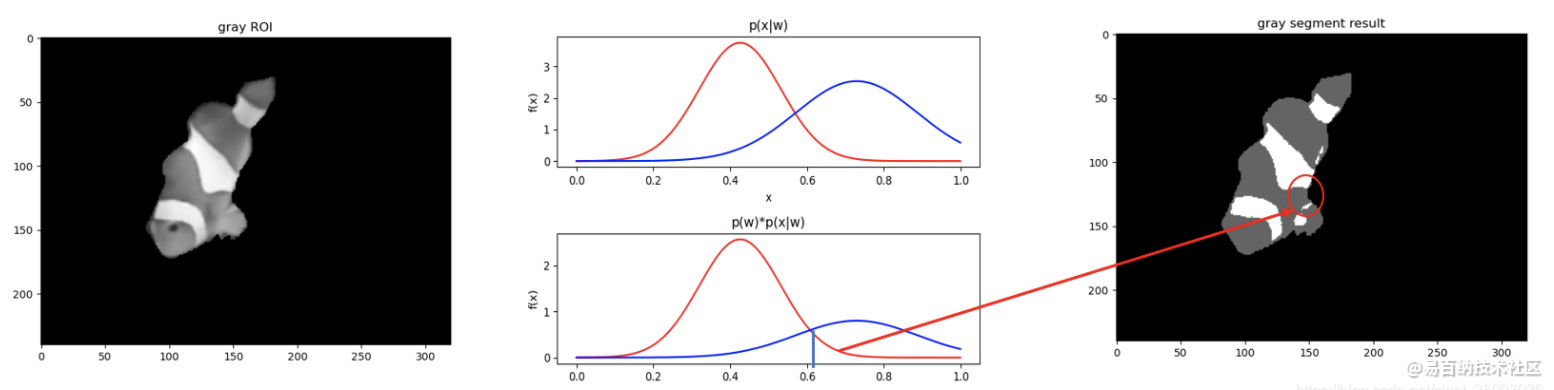
三维贝叶斯决策，计算三维输入时的贝叶斯后验概率。

# 三维时，贝叶斯
# ------------------------------------------------------------------------------------#
# 数据为三维时(彩色图像)，用最大似然估计两个类别条件概率pdf的参数——协方差与均值
RGB1_m = np.mean(RGB1, axis=0)
RGB2_m = np.mean(RGB2, axis=0)

cov_sum1 = np.zeros((3, 3))
cov_sum2 = np.zeros((3, 3))

for i in range(len(RGB1)):
    # print((RGB1[i]-RGB1_m).reshape(3, 1))
    cov_sum1 = cov_sum1 + np.dot((RGB1[i]-RGB1_m).reshape(3, 1), (RGB1[i]-RGB1_m).reshape(1, 3))

for i in range(len(RGB2)):
    cov_sum2 = cov_sum2 + np.dot((RGB2[i]-RGB2_m).reshape(3, 1), (RGB2[i]-RGB2_m).reshape(1, 3))

RGB1_cov = cov_sum1/(len(RGB1)-1)                      # 无偏估计除以N-1
RGB2_cov = cov_sum2/(len(RGB2)-1)

xx = np.array([x, x, x])
# print(P_pre1*multivariate_normal.pdf(RGB1, RGB1_m, RGB1_cov))

# 用最大后验贝叶斯对彩色图像进行分割
RGB_out = np.zeros_like(RGB_ROI)
for i in range(len(RGB_ROI)):
    for j in range(len(RGB_ROI[0])):
        if np.sum(RGB_ROI[i][j]) == 0:
            continue
        elif P_pre1*multivariate_normal.pdf(RGB_ROI[i][j], RGB1_m, RGB1_cov) > P_pre2*multivariate_normal.pdf(RGB_ROI[i][j], RGB2_m, RGB2_cov): # 贝叶斯公式分子比较
            RGB_out[i][j] = [255, 0, 0]
        else:
            RGB_out[i][j] = [0, 255, 0]
# print(RGB_ROI.shape)

# 显示RGB ROI，与彩色分割结果
plt.figure(3)
cx = plt.subplot(1, 1, 1)
cx.set_title('RGB ROI')
cx.imshow(RGB_ROI)
plt.figure(4)
cx1 = plt.subplot(1, 1, 1)
cx1.set_title('RGB segment result')
cx1.imshow(RGB_out)
plt.show()

3 Logistic回归

ogistic 回归 概述

Logistic 回归 或者叫逻辑回归 虽然名字有回归，但是它是用来做分类的。其主要思想是: 根据现有数据对分类边界线(Decision Boundary)建立回归公式，以此进行分类。

须知概念

Sigmoid 函数

回归 概念

假设现在有一些数据点，我们用一条直线对这些点进行拟合（这条直线称为最佳拟合直线），这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程，那么我们根据这个回归方程，怎么进行分类呢？请看下面。

二值型输出分类函数

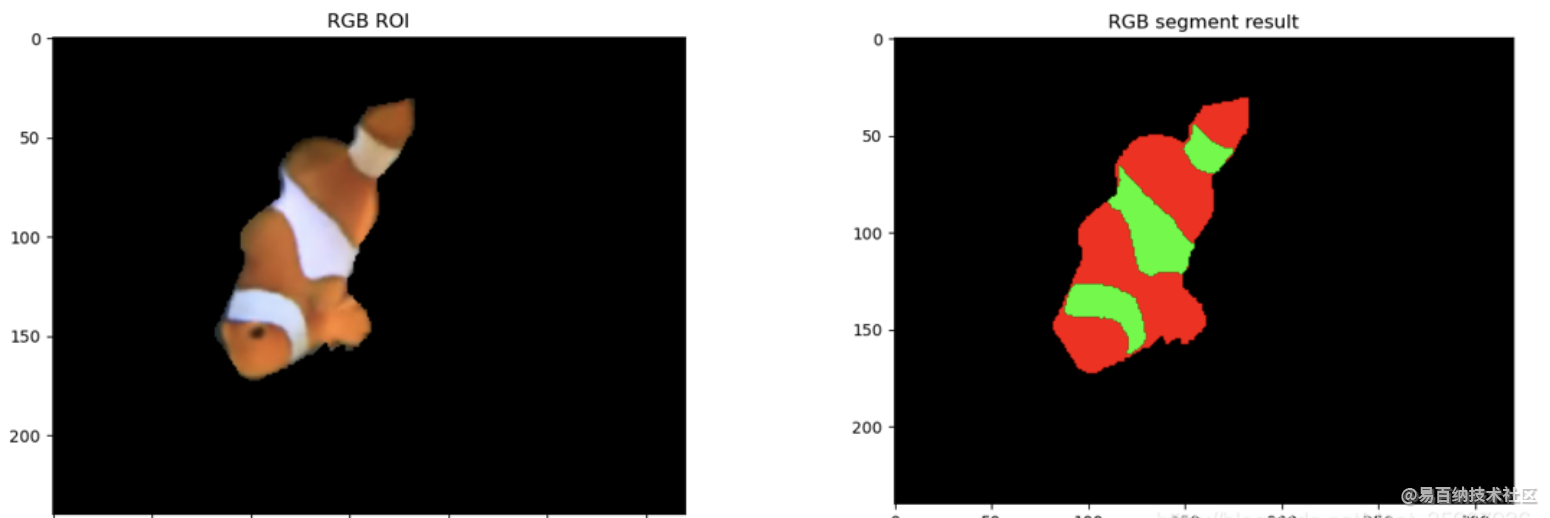
我们想要的函数应该是: 能接受所有的输入然后预测出类别。例如，在两个类的情况下，上述函数输出 0 或 1.或许你之前接触过具有这种性质的函数，该函数称为 海维塞得阶跃函数(Heaviside step function)，或者直接称为 单位阶跃函数。然而，海维塞得阶跃函数的问题在于: 该函数在跳跃点上从 0 瞬间跳跃到 1，这个瞬间跳跃过程有时很难处理。幸好，另一个函数也有类似的性质（可以输出 0 或者 1 的性质），且数学上更易处理，这就是 Sigmoid 函数。 Sigmoid 函数具体的计算公式如下:

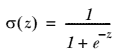
下图给出了 Sigmoid 函数在不同坐标尺度下的两条曲线图。当 x 为 0 时，Sigmoid 函数值为 0.5 。随着 x 的增大，对应的 Sigmoid 值将逼近于 1 ; 而随着 x 的减小， Sigmoid 值将逼近于 0 。如果横坐标刻度足够大， Sigmoid 函数看起来很像一个阶跃函数。

4 梯度上升法

梯度的介绍

需要一点点向量方面的数学知识

向量 = 值 + 方向
梯度 = 向量
梯度 = 梯度值 + 梯度方向
梯度上升法的思想

要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。如果梯度记为 ▽ ，则函数 f(x, y) 的梯度由下式表示:

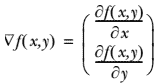
上图展示的，梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始，计算完该点的梯度，函数就根据梯度移动到下一点 P1。在 P1 点，梯度再次被重新计算，并沿着新的梯度方向移动到 P2 。如此循环迭代，直到满足停止条件。迭代过程中，梯度算子总是保证我们能选取到最佳的移动方向。

上图中的梯度上升算法沿梯度方向移动了一步。可以看到，梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向，而未提到移动量的大小。该量值称为步长
局部最优现象 （Local Optima）

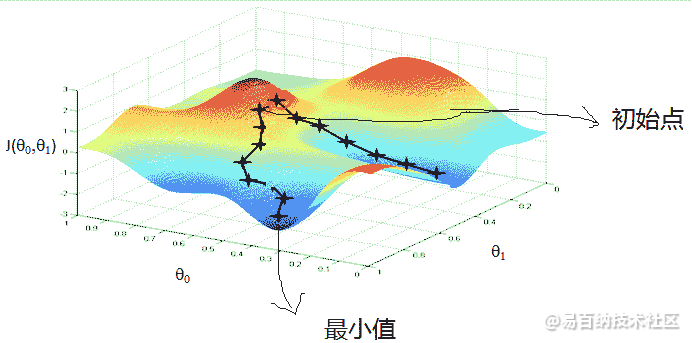
5 Logistic回归总结

Logistic 回归 工作原理

每个回归系数初始化为 1
重复 R 次:
计算整个数据集的梯度
使用 步长 x 梯度 更新回归系数的向量
返回回归系数
Logistic 回归 开发流程

收集数据: 采用任意方法收集数据
准备数据: 由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳。
分析数据: 采用任意方法对数据进行分析。
训练算法: 大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数。
测试算法: 一旦训练步骤完成，分类将会很快。
使用算法: 首先，我们需要输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定它们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作。
Logistic 回归 算法特点

优点: 计算代价不高，易于理解和实现。
缺点: 容易欠拟合，分类精度可能不高。
适用数据类型: 数值型和标称型数据。