【深度学习】softmax后处理和弹性形变前处理

【深度学习】softmax后处理和弹性形变前处理

文章目录
1 softmax的一个例子
2 后处理：通过平均来集成softmax概率
3 神经网络中的蒸馏技术，从Softmax开始说起
4 softmax加权集成
5 弹性形变前处理

1 softmax的一个例子

首先咱们先来规定一些参数,首先假设分割的前景目标一共有三种类别(行人, 车辆,红绿灯),分割图片的大小依然是200*200.那么题主在问题中描述的,40000个像素都各有一个值是不准确的,准确的说,是40000个像素都各有4个值,softmax之前以及之后的结果的对应tensor的shape都是(4, 200, 200),这里为什么第一个维度是4呢,因为有三种目标和一个背景,所以本分割任务相当于逐像素的在做四分类的问题,所以这时候想要得到最终的分割结果,应该对第一个维度也就是4那个维度取最大值,意思就是在每一个像素点,在四种类别中选取概率最高的那个类别。

1.函数用于卷积神经网络最后一层，对数据进行分类，不过该分类对每个可能结果都进行分类（小概率照样分类）：

定义：

假设有一个数组V，Vi 表示V中第i 个元素，

SoftMax就是该元素的指数与所有元素的指数和之比。

2.举例

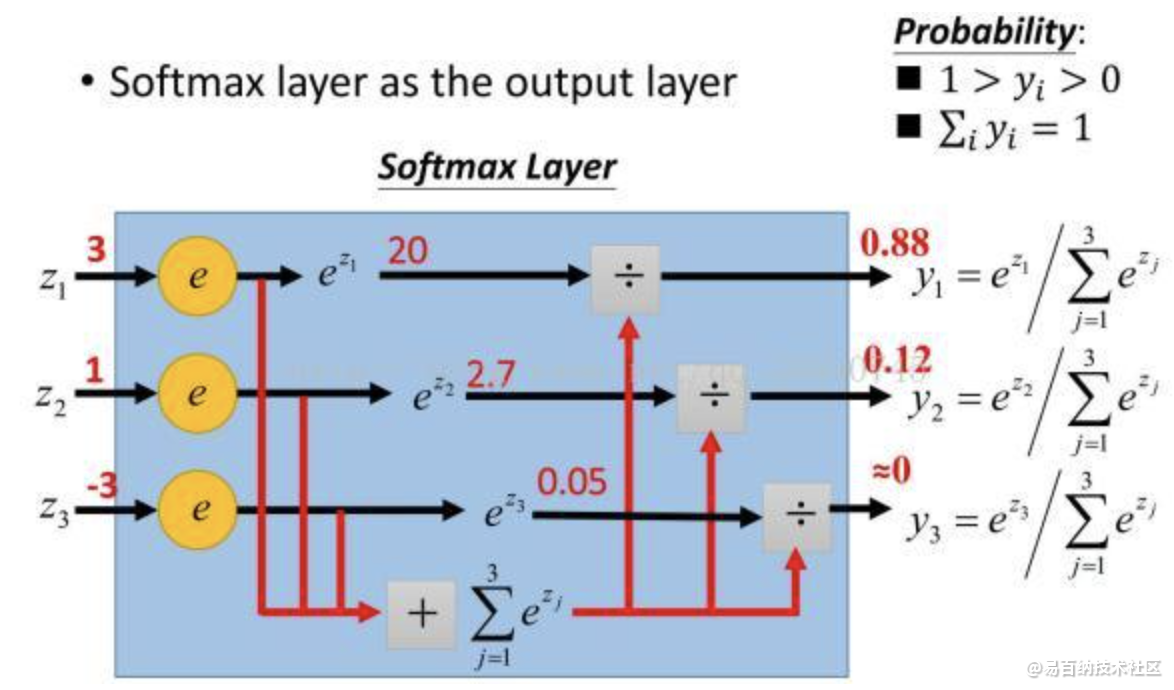
2 后处理：通过平均来集成softmax概率

传统的集成方法是集成几种不同的模型，再用相同的输入对模型进行预测，然后使用某种平均方法来确定集成模型的最终预测。平均方法 ( averaging ) 可以采用简单的投票方法 ( voting ) ，平均法或甚至使用集成模型中的一个模型去学习并预测输入的正确值或标签。岭回归 ( Ridge Regression ) 是一种特别的集成预测方式，也是被 Kaggle 竞赛冠军使用过的一种模型集成方法。

简单加权融合
  简单加权融合也叫做像素加权平均法（Weighted Averaging，WA）是最简单、直接的图像融合方法。它具有简单易实现、运算速度快的优点，并能提高融合图像的信噪比，但是这种方法削弱了图像中的细节信息，降低了图像的对比度，在一定程度上使得图像中的边缘变模糊，在多数应用场合难以取得满意的融合效果。

  优化：主成分分析(Principal Component Analysis，PCA)就是一种常用的系数优化方法，利用主成分分析确定的权值可以得到一幅亮度方差最大的融合图像。PCA方法运用于高分辨率全色图像与低分辨率多光谱图像的融合时，通过用高分辨率全色图像替代由低分辨率多光谱图像提取出的第一主成分，得到同时具有高空间分辨率和高光谱分。
　　
  从性能上讲，主成分分析法更像是对源图像的选择而不是对源图像中显著信息的融和。局限性：以全局方差作为信息显著性度量通常会把较大的权值分配给方差较大的源图像。实际应用中，当某一传感器输出图像对比度较低时，这种权值分配方法效果会比较好，但就一般情况而言，这种分配方法并不科学。此外，主成分分析法对图像中的死点、噪声等干扰信息非常敏感，这些干扰信息会显著的提高图像的全局方差。

function [y1,y2,y3]= jdfusion( x1,x2 )
%函数x= jdfusion( x1,x2 )实现基于加权平均的简单图像融合
%输入参数：
%      x1----输入原图像1
%      x2----输入原图像2
%输出参数：
%      y1----基于加权平均的融合图像
%      y2----基于像素值选大的融合图像
%      y3----基于像素值选小的融合图像
%----------------------------------------------------%
figure(1);imshow(x1);title('图像1');
figure(2);imshow(x2);title('图像2');
x1=double(x1);
x2=double(x2);
[m,n]=size(x1);

for i=1:m
    for j=1:n
        y1(i,j)=0.5*x1(i,j)+0.5*x2(i,j);  %基于加权平均的简单图像融合方法
    end
end

figure(3);imshow(uint8(y1));title('基于加权平均的融合图像');

for i=1:m
    for j=1:n
        if x1(i,j)>=x2(i,j)               %基于像素值选大的简单图像融合方法
            y2(i,j)=x1(i,j);
        else
            y2(i,j)=x2(i,j);
        end
    end
end

figure(4);imshow(uint8(y2));title('基于像素值选大的融合图像');

for i=1:m
    for j=1:n
        if x1(i,j)<x2(i,j)                %基于像素值选小的简单图像融合方法
            y3(i,j)=x1(i,j);
        else
            y3(i,j)=x2(i,j);
        end
    end
end

figure(5);imshow(uint8(y3));title('基于像素值选小的融合图像');

end

3 神经网络中的蒸馏技术，从Softmax开始说起

从各个层次给大家讲解模型的知识蒸馏的相关内容，并通过实际的代码给大家进行演示。

公众号后台回复“模型蒸馏”，下载已打包好的代码。

本报告讨论了非常厉害模型优化技术 —— 知识蒸馏，并给大家过了一遍相关的TensorFlow的代码。

“模型集成是一个相当有保证的方法，可以获得2%的准确性。“ —— Andrej Karpathy

我绝对同意！然而，部署重量级模型的集成在许多情况下并不总是可行的。有时，你的单个模型可能太大(例如GPT-3)，以至于通常不可能将其部署到资源受限的环境中。这就是为什么我们一直在研究一些模型优化方法 ——量化和剪枝。在这个报告中，我们将讨论一个非常厉害的模型优化技术 —— 知识蒸馏。
当处理一个分类问题时，使用softmax作为神经网络的最后一个激活单元是非常典型的用法。这是为什么呢？因为softmax函数接受一组logit为输入并输出离散类别上的概率分布。比如，手写数字识别中，神经网络可能有较高的置信度认为图像为1。不过，也有轻微的可能性认为图像为7。如果我们只处理像[1,0]这样的独热编码标签(其中1和0分别是图像为1和7的概率)，那么这些信息就无法获得。

人类已经很好地利用了这种相对关系。更多的例子包括，长得很像猫的狗，棕红色的，猫一样的老虎等等。正如Hinton等人所认为的

一辆宝马被误认为是一辆垃圾车的可能性很小，但被误认为是一个胡萝卜的可能性仍然要高很多倍。

这些知识可以帮助我们在各种情况下进行极好的概括。这个思考过程帮助我们更深入地了解我们的模型对输入数据的想法。它应该与我们考虑输入数据的方式一致。

所以，现在该做什么？一个迫在眉睫的问题可能会突然出现在我们的脑海中 —— 我们在神经网络中使用这些知识的最佳方式是什么？让我们在下一节中找出答案。
知识蒸馏的高层机制
所以，这是一个高层次的方法：

训练一个在数据集上表现良好神经网络。这个网络就是“教师”模型。

使用教师模型在相同的数据集上训练一个学生模型。这里的问题是，学生模型的大小应该比老师的小得多。

本工作流程简要阐述了知识蒸馏的思想。

为什么要小？这不是我们想要的吗？将一个轻量级模型部署到生产环境中，从而达到足够的性能。

用图像分类的例子来学习
对于一个图像分类的例子，我们可以扩展前面的高层思想：

训练一个在图像数据集上表现良好的教师模型。在这里，交叉熵损失将根据数据集中的真实标签计算。

在相同的数据集上训练一个较小的学生模型，但是使用来自教师模型(softmax输出)的预测作为ground-truth标签。这些softmax输出称为软标签。稍后会有更详细的介绍。

我们为什么要用软标签来训练学生模型？

请记住，在容量方面，我们的学生模型比教师模型要小。因此，如果你的数据集足够复杂，那么较小的student模型可能不太适合捕捉训练目标所需的隐藏表示。我们在软标签上训练学生模型来弥补这一点，它提供了比独热编码标签更有意义的信息。在某种意义上，我们通过暴露一些训练数据集来训练学生模型来模仿教师模型的输出。

希望这能让你们对知识蒸馏有一个直观的理解。在下一节中，我们将更详细地了解学生模型的训练机制。
扩展Softmax
这些弱概率的问题是，它们没有捕捉到学生模型有效学习所需的信息。例如，如果概率分布像[0.99, 0.01]，几乎不可能传递图像具有数字7的特征的知识。

Hinton等人解决这个问题的方法是，在将原始logits传递给softmax之前，将教师模型的原始logits按一定的温度进行缩放。这样，就会在可用的类标签中得到更广泛的分布。然后用同样的温度用于训练学生模型。

我们可以把学生模型的修正损失函数写成这个方程的形式：

其中，pi是教师模型得到软概率分布，si的表达式为：

def get_kd_loss(student_logits, teacher_logits,
true_labels, temperature,
alpha, beta):

teacher_probs = tf.nn.softmax(teacher_logits / temperature)
kd_loss = tf.keras.losses.categorical_crossentropy(
    teacher_probs, student_logits / temperature, 
    from_logits=True)

return kd_loss

使用扩展Softmax来合并硬标签
Hinton等人还探索了在真实标签(通常是独热编码)和学生模型的预测之间使用传统交叉熵损失的想法。当训练数据集很小，并且软标签没有足够的信号供学生模型采集时，这一点尤其有用。

当它与扩展的softmax相结合时，这种方法的工作效果明显更好，而整体损失函数成为两者之间的加权平均。

def get_kd_loss(student_logits, teacher_logits,
true_labels, temperature,
alpha, beta):
teacher_probs = tf.nn.softmax(teacher_logits / temperature)
kd_loss = tf.keras.losses.categorical_crossentropy(
teacher_probs, student_logits / temperature,
from_logits=True)

ce_loss = tf.keras.losses.sparse_categorical_crossentropy(
    true_labels, student_logits, from_logits=True)

total_loss = (alpha * kd_loss) + (beta * ce_loss)
return total_loss / (alpha + beta)

建议β的权重小于α。

在原始Logits上进行操作
Caruana等人操作原始logits，而不是softmax值。这个工作流程如下：

这部分保持相同 —— 训练一个教师模型。这里交叉熵损失将根据数据集中的真实标签计算。

现在，为了训练学生模型，训练目标变成分别最小化来自教师和学生模型的原始对数之间的平均平方误差。

mse = tf.keras.losses.MeanSquaredError()

def mse_kd_loss(teacher_logits, student_logits):
return mse(teacher_logits, student_logits)
使用这个损失函数的一个潜在缺点是它是无界的。原始logits可以捕获噪声，而一个小模型可能无法很好的拟合。这就是为什么为了使这个损失函数很好地适合蒸馏状态，学生模型需要更大一点。

Tang等人探索了在两个损失之间插值的想法：扩展softmax和MSE损失。数学上，它看起来是这样的：

根据经验，他们发现当α = 0时，(在NLP任务上)可以获得最佳的性能。

如果你在这一点上感到有点不知怎么办，不要担心。希望通过代码，事情会变得清楚。

4 softmax加权集成

1 什么是模型的集成？
集成方法是指由多个弱分类器模型组成的整体模型，我们需要研究的是：

① 弱分类器模型的形式
② 这些弱分类器是如何组合为一个强分类器
学习过机器学习相关基础的童鞋应该知道，集成学习有两大类——以Adaboost为代表的Boosting和以RandomForest为代表的Bagging。它们在集成学习中属于同源集成（homogenous ensembles）方法；而今天我将主要对一种目前在kaggle比赛中应用的较为广泛的集成方法——Stacked Generalization （SG），也叫堆栈泛化的方法（属于异源集成（heterogenous ensembles）的典型代表）进行介绍。

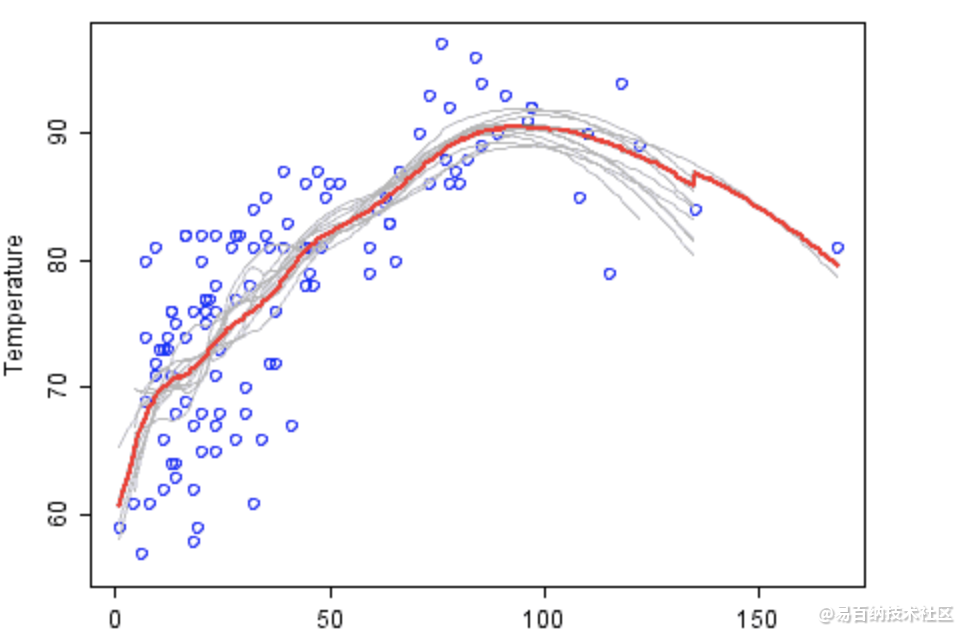
如上图，弱分类器是灰色的，其组合预测是红色的。图中展示的是温度——臭氧的相关关系。

2 堆栈泛化（Stacked Generalization）的概念
作为一个在kaggle比赛中高分选手常用的技术，SG在部分情况下，甚至可以让错误率相比当前最好的方法进一步降低30%之多。

以下图为例，简单介绍一个什么是SG：

① 将训练集分为3部分，分别用于让3个基分类器（Base-leaner）进行学习和拟合
② 将3个基分类器预测得到的结果作为下一层分类器（Meta-learner）的输入
③ 将下一层分类器得到的结果作为最终的预测结果

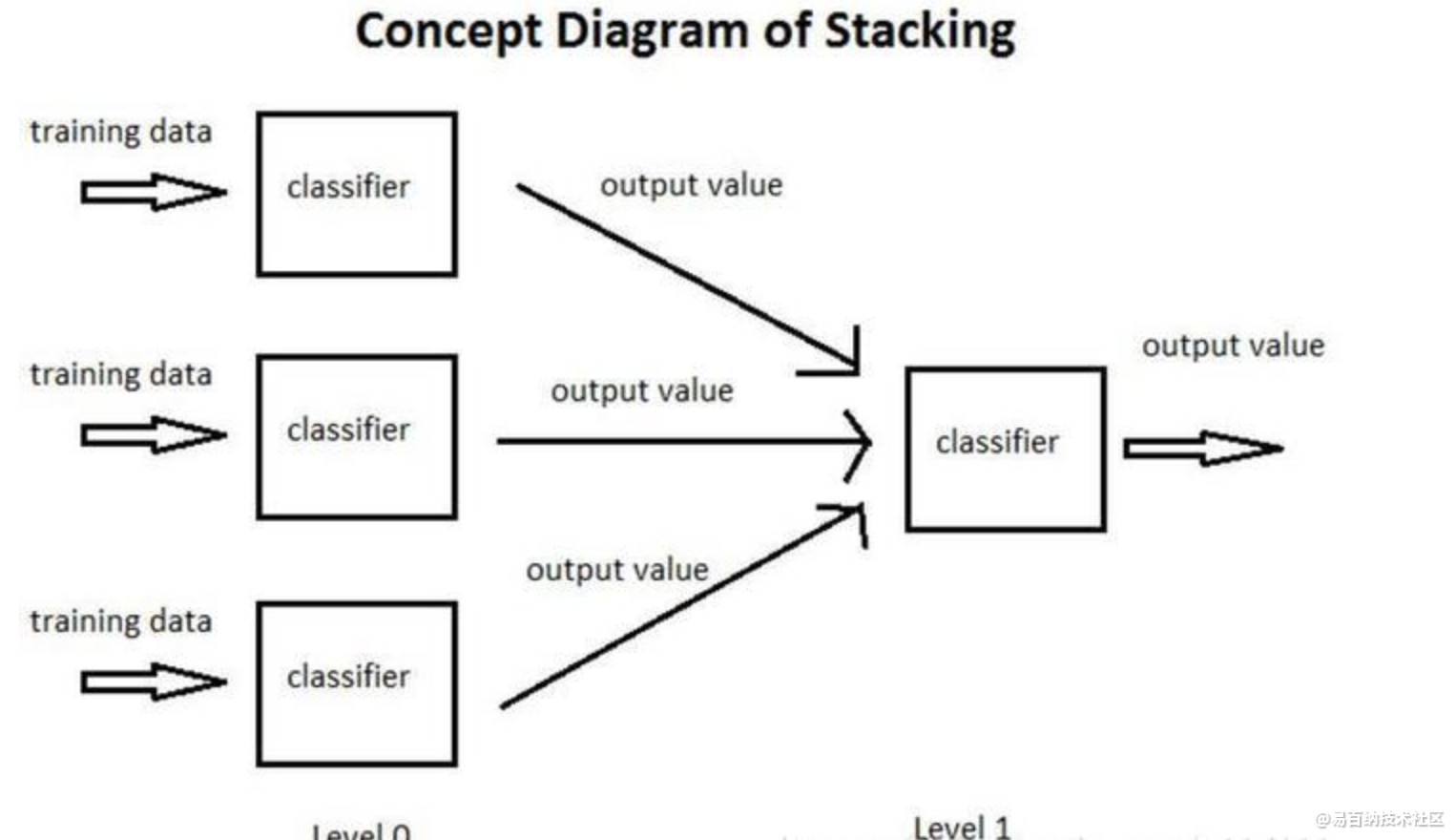
这个模型的特点就是通过使用第一阶段（level 0）的预测作为下一层预测的特征，比起相互独立的预测模型能够有更强的非线性表述能力，降低泛化误差。它的目标是同时降低机器学习模型的Bias-Variance。

总而言之，堆栈泛化就是集成学习（Ensemble learning）中Aggregation方法进一步泛化的结果， 是通过Meta-Learner来取代Bagging和Boosting的Voting/Averaging来综合降低Bias和Variance的方法。 譬如： Voting可以通过kNN来实现， weighted voting可以通过softmax（Logistic Regression）， 而Averaging可以通过线性回归来实现。

3 一个小例子
上面提到了同源集成经典方法中的Voting和Averaging，这里以分类任务为例，对Voting进行说明，那么什么是Voting呢？

Voting，顾名思义，就是投票的意思，假设我们的测试集有10个样本，正确的情况应该都是1：
我们有3个正确率为70%的二分类器记为A,B,C。你可以将这些分类器视为伪随机数产生器，即以70%的概率产生”1”，30%的概率产生”0”。

下面我们可以根据从众原理（少数服从多数），来解释采用集成学习的方法是如何让正确率从70%提高到将近79%的。

All three are correct
  0.7 * 0.7 * 0.7
= 0.3429

Two are correct
  0.7 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.7
= 0.4409

Two are wrong
  0.3 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.3
= 0.189

All three are wrong
  0.3 * 0.3 * 0.3
= 0.027

堆栈泛化的发展

最早重视并提出Stacking技术的是David H. Wolpert，他在1992年发表的论文Stacked Generalization
它可以看做是交叉验证（cross-validation）的复杂版， 通过胜者全得（winner-takes-all）的方式来进行集成的方法。

5 弹性形变前处理

仿射变换：
相当于对于图像做了一个平移、旋转、放缩、剪切、对称。与刚体变换相同的是，可以保持线点之间的平行和共线关系。即，原来平行的直线变化后还是平行的。但是和刚体变换不同的是线段之间的长度会发生变化。

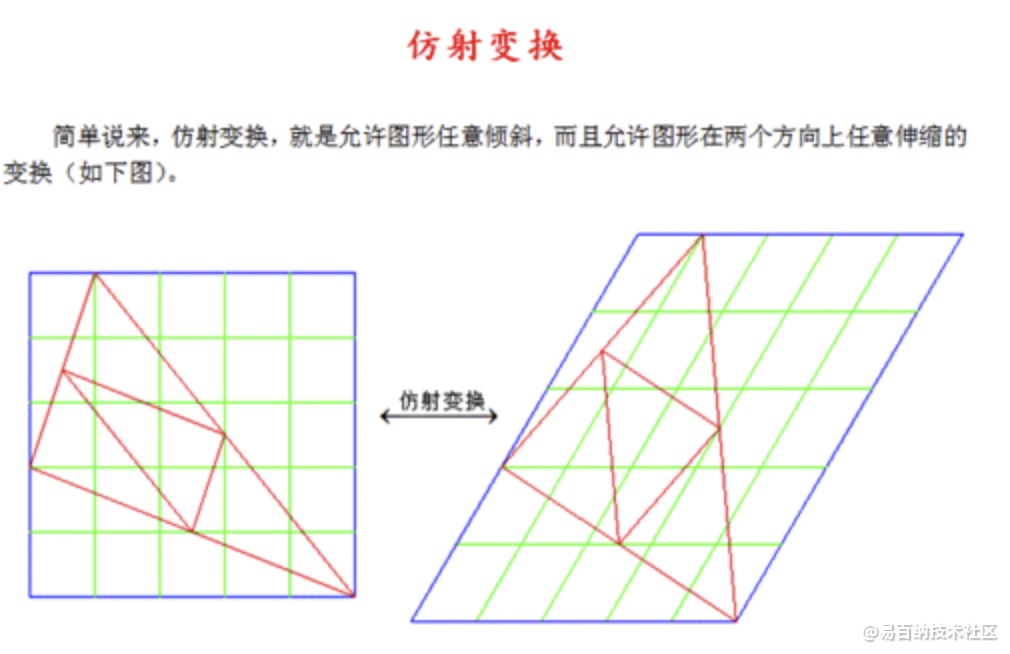
仿射变换是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。在有限维的情况，每个仿射变换可以由一个矩阵A和一个向量b给出，它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1。
设有图像A， 大小：M*N， 对于 任意像素（x1, y1）其变换为：
在python中用opencv实现：
由于变换矩阵的确定太过复杂，所以会采用3点去定法。即给出3个点在原图和变换后图像的位置，返回一个变换矩阵。pts1和pts2是3个点的list

    shape = image.shape
    shape_size = shape[:2]
    # Random affine
    center_square = np.float32(shape_size) // 2
    square_size = min(shape_size) // 3
    pts1 = np.float32([center_square + square_size, [center_square[0]+square_size, center_square[1]-square_size], center_square - square_size])
    pts2 = pts1 + random_state.uniform(-alpha_affine, alpha_affine, size=pts1.shape).astype(np.float32)
    M = cv2.getAffineTransform(pts1, pts2)
    image = cv2.warpAffine(image, M, shape_size[::-1], borderMode=cv2.BORDER_REFLECT_101)  

弹性变化：
弹性变换算法(Elastic Distortion)最先是由Patrice等人在2003年的ICDAR上发表的《Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis》提出的，最开始应用在mnist手写体数字识别数据集中，发现对原图像进行弹性变换的操作扩充样本以后，对于手写体数字的识别效果有明显的提升。此后成为一种很普遍的扩充字符样本图像的方式。

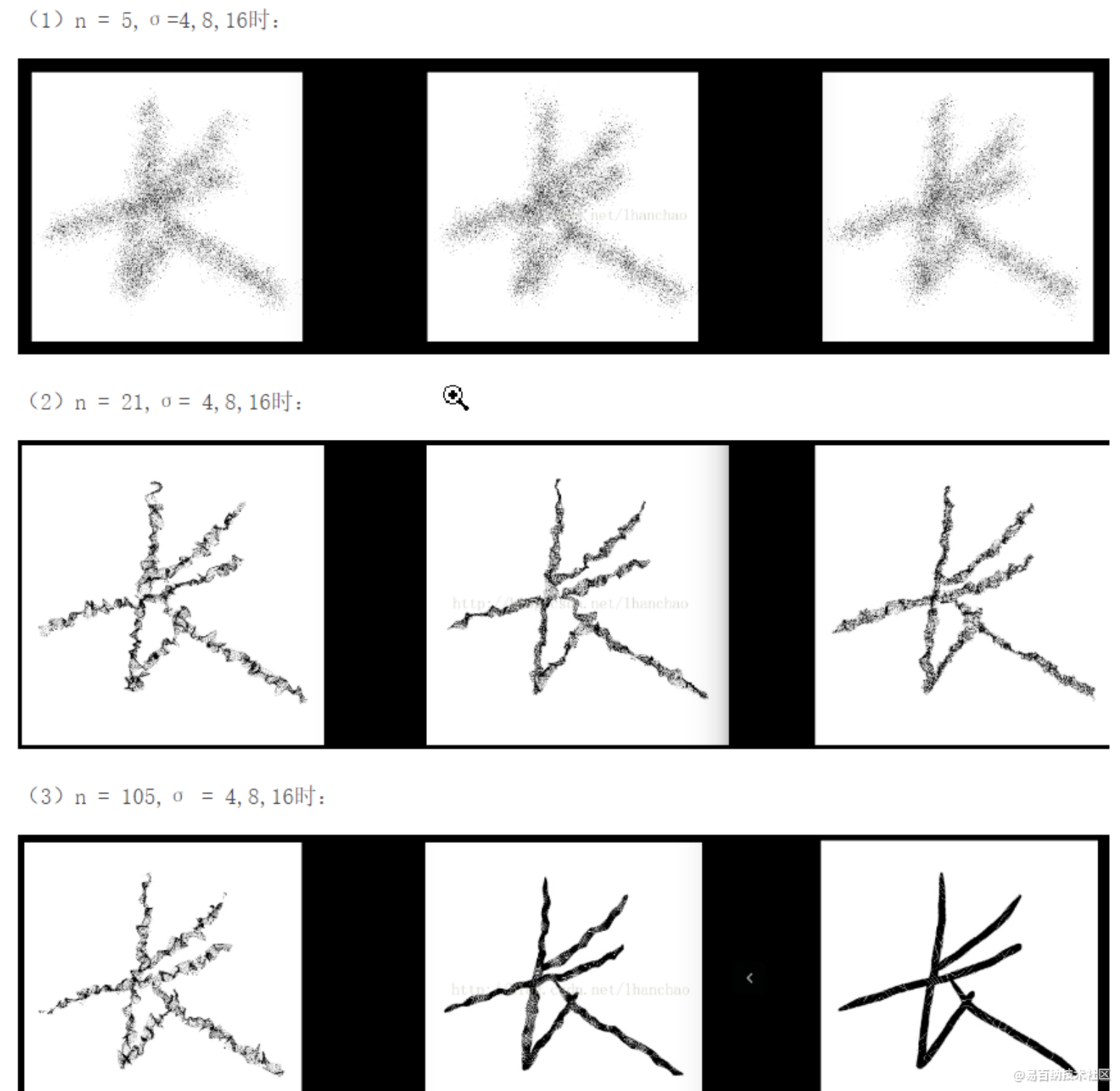
弹性变化是对像素点各个维度产生(-1，1)区间的随机标准偏差，并用高斯滤波（0，sigma）对各维度的偏差矩阵进行滤波，最后用放大系数alpha控制偏差范围。因而由A(x,y)得到的A’(x+delta_x,y+delta_y)。A‘的值通过在原图像差值得到，A’的值充当原来A位置上的值。一般来说，alpha越小，sigma越大，产生的偏差越小，和原图越接近。
代码实现：

import numpy as np
import pandas as pd
import cv2
from scipy.ndimage.interpolation import map_coordinates
from scipy.ndimage.filters import gaussian_filter
import matplotlib.pyplot as plt
def Elastic_transform(image, alpha, sigma):
    shape = image.shape
    shape_size = shape[:2]
    dx = gaussian_filter((random_state.rand(*shape) * 2 - 1), sigma) * alpha
    dy = gaussian_filter((random_state.rand(*shape) * 2 - 1), sigma) * alpha
    dz = np.zeros_like(dx)

    x, y, z = np.meshgrid(np.arange(shape[1]), np.arange(shape[0]), np.arange(shape[2]))
    indices = np.reshape(y+dy, (-1, 1)), np.reshape(x+dx, (-1, 1)), np.reshape(z, (-1, 1))

    return map_coordinates(image, indices, order=1, mode='reflect').reshape(shape)