【深度学习】快照集成等网络训练优化算法系列

【深度学习】快照集成等网络训练优化算法系列

文章目录
1 什么是快照集成?
2 什么是余弦退火学习率？
3 权重空间中的解决方案
4 局部与全局最优解
5 特别数据增强
6 机器学习中解决数据不平衡问题
    6.1 重新采样训练集
    6.2 使用K-fold交叉验证
7 集群丰富类

1 什么是快照集成?

快照集成一句话概括就是在同一个训练过程中，将不同节点的，且存在多样性的模型保存下来，再用于集成。这里有两个需要关注的点。

第一点是“同一个训练过程”。不同于一般的集成方法，快照集成不需要重新训练模型，而是在同一个训练过程中，产生成多个模型。我们知道，一个神经网络模型的训练时间很长。如果要训练多个模型，就需要更多时间和算力。快照集成的好处就是在不增加训练成本的前提下，仍然实现集成的效果。

第二点是“存在多样性的模型”。一般的集成方法之所有需要重新训练，就是为了保证模型的多样性，即预测错误的地方是不同的。正因为模型存在多样性，所以集成才能够比单个模型效果更好。而快照集成是如何使得同一训练过程中的模型存在多样性呢？这就需要了解余弦退火这个概念。

2 什么是余弦退火学习率？

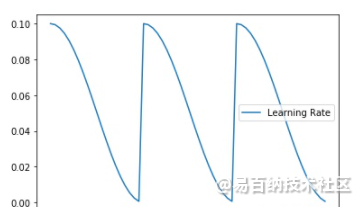
余弦退火学习率是一种在训练过程中，调整学习率的方法。余弦退火学习率不同于传统的学习率，随着epoch的增加，learning rate 先急速下降，再陡然提升，然后不断重复这个过程。
这样剧烈波动的目的在于：逃离当前的最优点。

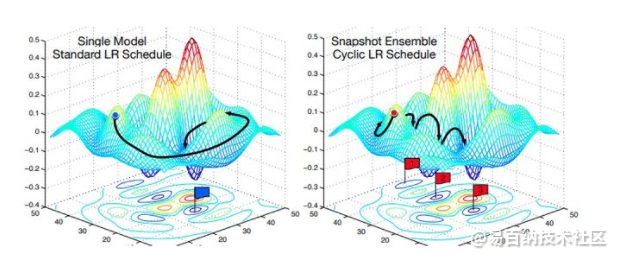
如上图左，传统的训练过程中学习率逐渐减小，所以模型逐渐找到局部最优点。这个过程中，因为一开始的学习率较大，模型不会踏入陡峭的局部最优点，而是快速往平坦的局部最优点移动。随着学习率逐渐减小，模型最终收敛到一个比较好的最优点。

如上图右，由于余弦退火的学习率急速下降，所以模型会迅速踏入局部最优点（不管是否陡峭），并保存局部最优点的模型。⌈快照集成⌋中⌈快照⌋的指的就是这个意思。保存模型后，学习率重新恢复到一个较大值，逃离当前的局部最优点，并寻找新的最优点。因为不同局部最优点的模型则存到较大的多样性，所以集合之后效果会更好。

两种方式比较起来，可以理解为模型训练的“起点”和“终点”是差不多的。不同的是，余弦退火学习率使得模型的训练过程比较“曲折”。

3 权重空间中的解决方案

第一个重要的观点是：一个训练好的网络是多维权重空间中的一个点。对于一个给定的网络结构，每一种不同的权重组合将得到不同的模型。因为所有模型结构都有无限多种权重组合，所以将有无限多种组合方法。训练神经网络的目标是找到一个特别的解决方案（权重空间中的点），从而使训练集和测试集上的损失函数的值达到很小。

训练过程中，通过改变权重，训练算法改变网络的结构，并在权重空间中不断搜索。随机梯度下降法在损失平面上传播，损失平面的高低由损失函数的值决定。

4 局部与全局最优解

可视化与理解多维权重空间的几何特点是非常困难的。同时，这也是非常重要的，因为在训练时，随机梯度下降法的本质是在多维空间的损失平面上传播，并努力找到一个好的解决方案--损失平面上的一个损失函数值很低的"点”。众所周知，这些平面有许多局部最优解，但并不是所有局部最优解都是优秀的解决方案。

局部和全局最优解。在训练和测试过程中，平滑的最低值会产生相似的损失。然而，训练和测试过程中产生的局部损失，有非常大的差异。换句话说，全局最小值比局部最小值更通用。

判断解决方案好坏的一个标准就是该方案解的平滑性。 这一思想在于训练数据和测试数据会产生类似的但并不完全一样的损失面。你可以想象一下，一个测试表面相对于训练表面移动一点。对于一个局部解，在测试过程中，因为这一点移动，一个给出低损失值的点会给出一个高损失值。这意味着这个”局部“解决方案没有产生最优值——训练损失小，而测试损失大。另一方面，对于一个”全局“平滑解决方案，这一点移动会导致训练和测试损失的差值很小。

5 特别数据增强

   对于UNet_cascade的full_resolution_UNet来说，额外对low_resolution_3D_UNet生成的mask采用下面的增强方法。注意这个mask是按独热编码进行保存的。

1. 二值操作
   对所有的labels以0.4的概率进行这个二值操作，这个操作是从膨胀、腐蚀、开操作、闭操作中随机选取的。结构元素是一个半径为r ~ U(1,8)的球体。该操作以随机顺序应用于标签。因此，独热编码特性被保留。例如，一个标签的膨胀会导致膨胀区域的所有其他标签被移除。
2. 小连接分支移除
   小于15% patch大小的连通分支以0.2的概率从独热编码中移除。

   6 机器学习中解决数据不平衡问题

   在机器学习中我们经常会遇到数据不平衡问题。数据不平衡主要存在于有监督机器学习任务中。当遇到数据不平衡时，以总体分类准确率为学习目标的传统分类算法会过多地关注多数类，从而使得少数样本的分类性能下降。绝大多数常见的机器学习算法对于不平衡数据集都不能很好地工作。
   本文主要介绍几种有效的解决数据不平衡情况下有效训练有监督算法的思路。

6.1 重新采样训练集

可以使用不同的数据集。有两种方法使不平衡的数据集来建立一个平衡的数据集——欠采样和过采样。

1.1 欠采样
欠采样是通过减少丰富类的大小来平衡数据集，当数据量足够时就该使用此方法。通过保存所有稀有类样本，并在丰富类别中随机选择与稀有类别样本相等数量的样本，可以检索平衡的新数据集以进一步建模。

1.2 过采样
相反，当数据量不足时就应该使用过采样，它尝试通过增加稀有样本的数量来平衡数据集，而不是去除丰富类别的样本的数量。通过使用重复、自举或合成少数类过采样等方法（SMOTE）来生成新的稀有样品。

注意：欠采样和过采样这两种方法相比而言，都没有绝对的优势。这两种方法的应用取决于它适用的用例和数据集本身。另外将过采样和欠采样结合起来使用也是成功的。

6.2 使用K-fold交叉验证

值得注意的是，使用过采样方法来解决不平衡问题时应当适当地应用交叉验证。这是因为过采样会观察到罕见的样本，并根据分布函数应用自举生成新的随机数据，如果在过采样之后应用交叉验证，那么我们所做的就是将我们的模型过拟合于一个特定的人工引导结果。这就是为什么在过度采样数据之前应该始终进行交叉验证，就像实现特征选择一样。只有重复采样数据可以将随机性引入到数据集中，以确保不会出现过拟合问题。

K-fold交叉验证就是把原始数据随机分成K个部分，在这K个部分中选择一个作为测试数据，剩余的K-1个作为训练数据。交叉验证的过程实际上就是将实验重复做K次，每次实验都从K个部分中选择一个不同的部分作为测试数据，剩余的数据作为训练数据进行实验，最后把得到的K个实验结果平均。

1.为什么不直接拆分训练集与数据集，来验证模型性能，反而采用多次划分的形式，岂不是太麻烦了？

我们为了防止在训练过程中，出现过拟合的问题，通行的做法通常是将数据分为训练集和测试集。测试集是与训练独立的数据，完全不参与训练，用于最终模型的评估。这样的直接划分会导致一个问题就是测试集不会参与训练，这样在小的数据集上会浪费掉这部分数据，无法使模型达到最优（数据决定了程性能上限，模型与算法会逼近这个上限）。但是我们又不能划分测试集，因为需要验证网络泛化性能。采用K-Fold 多次划分的形式就可以利用全部数据集。最后采用平均的方法合理表示模型性能。

2.为什么还要进行所有数据集重新训练，是否太浪费时间？

我们通过K-Fold 多次划分的形式进行训练是为了获取某个模型的性能指标，单一K-Fold训练的模型无法表示总体性能，但是我们可以通过K-Fold训练的训练记录下来较为优异的超参数，然后再以最优模型最优参数进行重新训练，将会取得更优结果。

也可以采取方法一的方式不再进行训练使用模型融合的方式。

3.何时使用K-Fold

我的看法，数据总量较小时，其他方法无法继续提升性能，可以尝试K-Fold。其他情况就不太建议了，例如数据量很大，就没必要更多训练数据，同时训练成本也要扩大K倍（主要指的训练时间）。
交叉验证是用于估计机器学习模型技能的统计方法。也是一种用于评估有限数据样本的机器学习模型的重采样方法。该方法简单且易于理解。K-Fold将将数据集拆分为k个部分。每次使用k-1个部分当做训练集，剩下的一个部分当做验证集进行模型训练，即训练K次模型。其具体步骤如下：

7 集群丰富类

Sergey Quora提出了一种优雅的方法，他建议不要依赖随机样本来覆盖训练样本的种类，而是将r个群体中丰富类别进行聚类，其中r为r中的例数。每个组只保留集群中心(medoid)。然后，基于稀有类和仅保留的类别对该模型进行训练。

7.1 对丰富类进行聚类操作

首先，我们可以对具有大量样本的丰富类进行聚类操作。假设我们使用的方法是K-means聚类算法。此时，我们可以选择K值为稀有类中的数据样本的个数，并将聚类后的中心点以及相应的聚类中心当做富类样本的代表样例，类标与富类类标一致。

7.2 聚类后的样本进行有监督学习
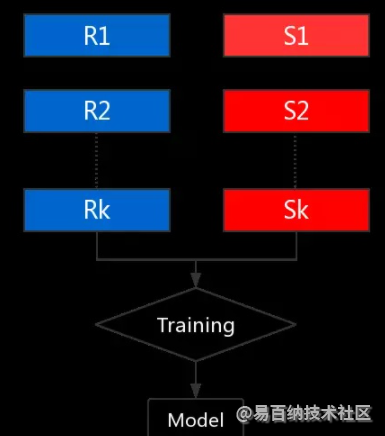
经过上述步骤的聚类操作，我们对富类训练样本进行了筛选，接下来我们就可以将相等样本数的K个正负样本进行有监督训练，如下图所示: