【深度学习】模式识别技术探索之决策树（Decision tree）

【深度学习】模式识别技术探索之决策树（Decision tree）

文章目录
1 什么是模式和模式识别？
2 常见的模式识别系统
3 应用领域
4 举例：随机森林（Random Forest）
    4.1 基本思想
    4.2 决策树 – Decision tree
    4.3 3 种典型的决策树算法
4.4 实现

1 什么是模式和模式识别？

当我们人眼看到一幅画时，我们能够很清晰的知道其中哪里是动物，哪里是山，水，人等等，但是人眼又是如何识别和分辨的呢，其实很简单，人类也是在先验知识和对以往多个此类事物的具体实例进行观察的基础上得到的对此类事物整体性质和特点的认识的，并不是人类原本就有对这类事物的记忆，就好比婴孩时期的我们，并不知道什么是狗，什么是帅哥，什么是meinv，但是随着我们的慢慢长大，我们观察的多了，见的多了，再加上过来人的经验指导，我们就知道的多了，也懂得的多了，就觉得自己很牛逼了。
其实，每一种外界的事物都是一种模式，人类平均每天都在进行着很多很多的各种各样的模式识别，人们对外界事物的识别，很大部分是把事物进行分类来完成的；那么如何让机器活计算机做到人眼这么牛逼呢，哪怕是达到人眼识别的10%也好啊，哈哈，答案显而易见了，模仿人眼的分类啊。

《说文》中记载，模，法也；式，法也。可以看出，模和式的意思是一样的，简单来说就是一种规律；而在英文中，模式pattern这个词的意思有两层，第一层是代表事物（个体或一组事物）的模板或原型；第二层是表征事物特点的特征或性状的组合。在模式识别学科中，模式可以看做是对象的组成成分或影响因素间存在的规律性关系，或者是因素间存在的确定性或随机性规律的对象、过程或事件的集合。因此，也有人把模式成为模式类，模式识别也被称作为模式分类（Pattern Classification）。

模式识别作为一门交叉学科，其研究的重点不是人类进行模式识别的神经生理学或生物学原理，而是研究如何通过一系列数学方法让机器来实现类人的识别能力。这是我们的长期奋斗目标，也是有着极大研究意义的学科，希望它能够在各专家和学者的不懈努力下实现更大的突破。

    这里，要记住一些模式识别的专业术语：

    样本（sample），要研究对象的一个个体，注意与统计学中的不同，类似于统计学中的实例（instance）；

    样本集（sample set），样本的集合，统计学中的样本就是指样本集；

    类或类别（class），在所有样本上定义的一个子集，处于同一类的样本，我们说她们具有相同的模式；习惯性地，我们用w1，w2等来表示类别，两类问题中也会用{0,1}或{-1,1}；

    特征（feature），表征样本的特点或性状的量化集合，通常是数值表示（对于非数值形式，要转化为数值特征），也被称作为属性，如果是多个特征，就组成了特征向量（feature vector）。样本的特征构成了样本特征空间，空间的维数就是特征的个数，每一个样本就是特征空间中的一个点。

   已知样本（known sample），已经事先知道类别的样本；

   未知样本（unknown sample），类别标签未知但特征已知的样本；

2 常见的模式识别系统

主要有：语音识别，说话人识别，OCR，复杂图像中特定目标的识别，根据地震勘探数据对地下储层性质的识别，利用基因表达数据进行癌症的分类等等；
计算机识别的显著特点是速度快、准确性高、效率高，在将来完全可以取代人工录入。

识别过程与人类的学习过程相似。以光学识别“中华文化”为例：首先将汉字图像进行处理，抽取主要表达特征并将特征与汉字的代码存在计算机中。就像老师教我们“这个字叫什么、如何写”记在大脑中。这一过程叫做“训练”。识别过程就是将输入的汉字图像经处理后与计算机中的所有字进行比较，找出最相近的字就是识别结果。这一过程叫做“匹配”

3 应用领域

1.计算机视觉

医学影像分析
光学文字识别
2.自然语言处理

语音识别
手写识别
3.生物特征识别

人脸识别
指纹识别
虹膜识别

4.文字分类

5.搜索引擎

6.信用测分

7.测绘学

摄影测量与遥感学

4 举例：随机森林（Random Forest）

模式识别是一门基于数据的学科，因此所有的模式识别问题都会面临的同一个问题就是数据的随机性问题。模式识别中每个方法的实现都是基于一个特定的数据样本集的，但是这个样本集只是所有可能的样本中的一次随机抽样，毕竟在我们的生活实际中存在着万物众生，多到我们数也数不清，甚至计算机都无法统计的清，而我们搜集到的充其量只是其中很小很小的一部分，这也是为什么机器学习中缺少的只是数据，只要有足够多的学习数据，就一定能取得惊人的结果，因此模式识别和机器学习中的很多方法的实现结果都无疑会受到这种随机性的影响，我们训练得到的分类器也因此具有偶然性，尤其是样本不足够多时更为明显。

   对于决策树而言，其树的生长是采用的贪心算法，只考虑当前局部的最优，因此其受这种随机性影响会更加严重，这也是为什么有的决策树泛化能力那么差的原因。

   针对这种随机性的影响，最早在统计学中有人提出了一种叫做”自举（Bootstrap）“的策略，基本思想是对现有样本进行重复采样而产生多个样本子集，通过这种多次重复采样来模拟数据的随机性，然后在最后的输出结果中加进去这种随机性的影响。随后有人把这种自举的思想运用到了模式识别中，衍生出了一系列的解决方法，像随机森林、Bagging、Adaboost等，这篇博客就来学习下什么是随机森林

4.1 基本思想

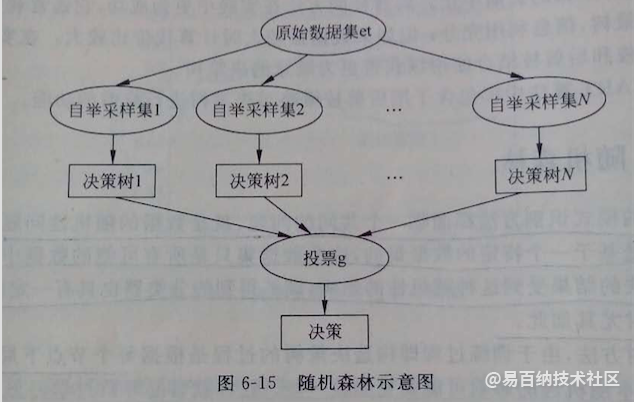
随机森林是以决策树为基础的，从其名字”森林“俩字可以看出肯定有很多个什么鬼组成的一片茂密的大森林啊，那到底是什么鬼捏，其实就是决策树；随机森林其实就是建立很多个决策树，组建成决策树”森林“，然后通过对多个决策树投票来进行决策，通常决策为投票最多的。随机森林跟C4.5算法一样，不光可以处理离散数值特征，而且可以处理连续数值特征，这是ID3算法所不具备的。

1）根据实际需要，得出需要构造的决策树数目T；

2）首先对样本数据进行自举重采样，生成多个样本子集；什么是自举重采样，就是高中学概率问题的时候接触到最多的有放回问题，即每次从N个样本中有放回的随机取出一个，这样取N次，最后会得到N个样本，当然有可能取到重复样本，但是没关系；

3）随机抽取用来构造决策树的特征：每次从所有候选特征中随机的选出m个特征，作为当前节点下决策用的备选特征，然后根据比较信息增益的方法选取出可以最好划分训练样本的特征；

4）利用上述已经选好的代表性特征，将每个重采样的样本集作为训练样本构造决策树；

5）得到事先给定的决策树数目的众多决策树后，分别对每棵树的输出结果进行投票，将票数最多的类决策为随机森林最后的决策；

上述原理如图所示，一目了然：

4.2 决策树 – Decision tree

决策树是一种解决分类问题的算法，

决策树算法采用树形结构，使用层层推理来实现最终的分类。决策树由下面几种元素构成：

根节点：包含样本的全集
内部节点：对应特征属性测试
叶节点：代表决策的结果

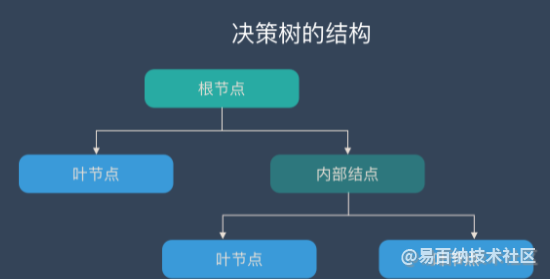
预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。

这是一种基于 if-then-else 规则的有监督学习算法，决策树的这些规则通过训练得到，而不是人工制定的。

决策树是最简单的机器学习算法，它易于实现，可解释性强，完全符合人类的直观思维，有着广泛的应用。

举个栗子：

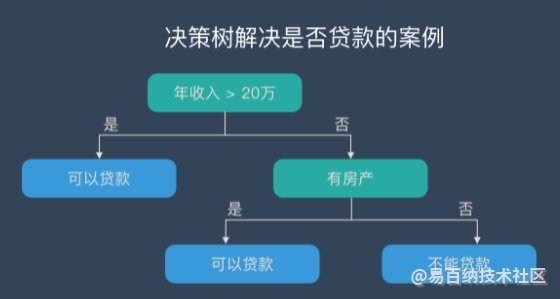
上面的说法过于抽象，下面来看一个实际的例子。银行要用机器学习算法来确定是否给客户发放daikuan，为此需要考察客户的年收入，是否有房产这两个指标。领导安排你实现这个算法，你想到了最简单的线性模型，很快就完成了这个任务。

决策树学习的 3 个步骤

特征选择

特征选择决定了使用哪些特征来做判断。在训练数据集中，每个样本的属性可能有很多个，不同属性的作用有大有小。因而特征选择的作用就是筛选出跟分类结果相关性较高的特征，也就是分类能力较强的特征。

在特征选择中通常使用的准则是：信息增益。

决策树生成

选择好特征后，就从根节点触发，对节点计算所有特征的信息增益，选择信息增益最大的特征作为节点特征，根据该特征的不同取值建立子节点；对每个子节点使用相同的方式生成新的子节点，直到信息增益很小或者没有特征可以选择为止。

决策树剪枝

剪枝的主要目的是对抗「过拟合」，通过主动去掉部分分支来降低过拟合的风险。

4.3 3 种典型的决策树算法

ID3 算法

ID3 是最早提出的决策树算法，他就是利用信息增益来选择特征的。

C4.5 算法

他是 ID3 的改进版，他不是直接使用信息增益，而是引入“信息增益比”指标作为特征的选择依据。

CART（Classification and Regression Tree）

这种算法即可以用于分类，也可以用于回归问题。CART 算法使用了基尼系数取代了信息熵模型。

决策树的优缺点
优点

决策树易于理解和解释，可以可视化分析，容易提取出规则；
可以同时处理标称型和数值型数据；
比较适合处理有缺失属性的样本；
能够处理不相关的特征；
测试数据集时，运行速度比较快；
在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
缺点

容易发生过拟合（随机森林可以很大程度上减少过拟合）；
容易忽略数据集中属性的相互关联；
对于那些各类别样本数量不一致的数据，在决策树中，进行属性划分时，不同的判定准则会带来不同的属性选择倾向；信息增益准则对可取数目较多的属性有所偏好（典型代表ID3算法），而增益率准则（CART）则对可取数目较少的属性有所偏好，但CART进行属性划分时候不再简单地直接利用增益率尽心划分，而是采用一种启发式规则）（只要是使用了信息增益，都有这个缺点，如RF）。
ID3算法计算信息增益时结果偏向数值比较多的特征。

4.4 实现

利用训练数据，训练决策树，主要思路如下，共8个步骤，重点在于递归：

自定义信息熵计算函数，用于计算数据集的信息熵
自定义数据划分函数，用于根据指定特征的指定取值，划分数据集
step2的自数据集作为输入给step1的函数，可以计算出按某指定特征的某指定取值(A=ai)划分的数据集的信息熵H(Di)，同时计算按某指定特征的某指定取值(A=ai)划分的数据集的样本概率|Di|/|D|
遍历该特征各个取值，计算各取值下划分的数据集的信息熵H(Di)和样本概率|Di|/|D|，相乘，再求和得到得到特征A对数据集D的经验条件熵H(D|A)
计算特征A对数据集的信息增益g(D,A)=H(D)-H(D|A)
以此类推，计算各特征对数据集的信息增益，取信息增益最大的特征为最佳划分特征，得到树T1
对T1各结点继续step3-6,选择信息增益最大的特征，继续划分数据，得到新的决策树
直到信息增益小于阈值，或无特征可划分，或每个分支下的所有实例都具有相同的分类，决策树完成

step1 自定义信息熵计算函数，用于计算数据集的信息熵

"""
输入：数据集，每一行是一条数据，最后一列是各条数据集的类别
输出：该数据集的信息熵
思路：
建立一个字典，对数据集各数据的类别计数，
从而计算各类别出现频率(作为概率pi)，
最后调用信息熵公式计算 H(D)=-求和(pi*logpi)
"""
def calEntropy(dataset):
n=len(dataset)
labelCounts={}

#对数据集各数据的类别计数
for data in dataset:
    datalabel=data[-1] #取data最后一列，类别列
    if datalabel not in labelCounts.keys():
        labelCounts[datalabel]=0
    labelCounts[datalabel]+=1

entropy=0.0

#计算各类别出现频率(作为概率pi),调用信息熵公式计算 H(D)=-求和(pi*logpi)
for key in labelCounts.keys():
    prob=float(labelCounts[key])/n
    entropy -= prob*log(prob,2)
return entropy

step2 自定义数据划分函数，用于根据指定特征的指定取值，划分数据集

"""
输入：数据集、特征所在列索引、特征取值
输出：满足指定特征等于指定取值的数据子集
"""
def splitDataset(dataset,index,value):
subDataset=[]
for data in dataset:
if data[index]==value:

抽取除了data[index]的内容(一个特征用于计算其对数据集的经验条件熵时，不需要此特征在子数据集中)

        splitData=data[:index] #取索引之前的元素
        splitData.extend(data[index+1:]) #再合并索引之后的元素
        subDataset.append(splitData)
return subDataset

step3~6 选择信息增益最大的特征作为数据集划分特征

"""
输入：数据集
输出：该数据集的最佳划分特征
"""
def chooseFeature(dataset):

初始化

numFeature=len(dataset[0])-1 #因为最后一列是类别
baseEntropy=calEntropy(dataset) #H(D)
bestInfoGain=0.0
bestFeatureIndex=-1

#创建特征A各取值a的列表
for i in range(numFeature):
    featureList=[data[i] for data in dataset]
    uniqueValue=set(featureList)
    empEntropy=0.0 #初始化特征A对数据集D的经验条件熵H(D|A)

    #计算特征A各取值a的信息熵H(Di)和样本概率|Di|/|D|，并相乘
    for value in uniqueValue:
        subDataset=splitDataset(dataset,i,value) #(列索引为i的特征)特征A取value值所划分的子数据集
        prob=len(subDataset)/float(len(dataset)) #计算|Di|/|D|
        empEntropy += prob*calEntropy(subDataset) #H(D|A)

    #取信息增益最大的特征为最佳划分特征
    infoGain=baseEntropy-empEntropy #信息增益
    if infoGain>bestInfoGain:
        bestInfoGain=infoGain
        bestFeatureIndex=i
return bestFeatureIndex

step7~8 递归构建决策树

def majorClass(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1

#对classCount按value降序排序
sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0] #返回类别最大的类别名

"""
输入：数据集(list类型)，数据集特征列表(按在数据集的位置排序)(list类型)
输出：该数据集的决策树
思路：【递归】

1. 若数据集属于同一类，则返回该类别，划分停止
2. 若数据集所有特征已经遍历，返回当前计数最多的类别为该结点类别，划分停止
3. 否则继续分支，调用chooseFeature()函数，选择当前数据集最优特征
4. 遍历当前最优特征各属性值，划分数据集，并递归调用自身createTree()构建子数据集的决策树

5. 完成
   """
   def createTree(dataset,featureLabels):
   classList=[data[-1] for data in dataset] #取数据集各数据类别

   若数据集属于同一类，则返回该类别，划分停止

   if classList.count(classList[0])==len(classList):
   return classList[0]

   若数据集所有特征已经遍历，返回当前计数最多的类别为该结点类别，划分停止

   if len(dataset[0])==1:
   return majorClass(classList)

   否则继续分支，调用chooseFeature()函数，选择当前数据集最优特征

   bestFeatureIndex=chooseFeature(dataset)
   bestFeature=featureLabels[bestFeatureIndex]

   用于存储决策树，字典结构存储树的所有信息，并可体现包含关系

   desitionTree={bestFeature:{}}
   del(featureLabels[bestFeatureIndex]) #删除已被用于划分数据的特征

   得到当前最优划分特征的各属性值

   featureValues=[data[bestFeatureIndex] for data in dataset]
   uniqueValues=set(featureValues)

   遍历当前最优特征各属性值，划分数据集，并递归调用自身createTree()构建子数据集的决策树

   for value in uniqueValues:

   得到已删除当前最优划分特征的特征列表,用于递归调用

   subFeatureLabels=featureLabels[:] 
   
   #用当前最优划分特征的指定值分割子数据集，用于递归调用
   subData=splitDataset(dataset,bestFeatureIndex,value) 
   desitionTree[bestFeature][value]=createTree(subData,subFeatureLabels)

   return desitionTree
   至此，决策树训练函数完成，下面我们利用西瓜分类数据集来简单测试一下吧~

04 测试

西瓜分类数据集长这样，基于西瓜的各个特征，判断西瓜是好瓜还是坏瓜：

我们直接调用刚才写好的决策树训练函数，看看西瓜分类数据的决策树吧

watermalon=pd.read_csv(r"D:\python\data\watermalon.txt",sep="\t")
watermalon_list=np.array(watermalon).tolist() #构建数据集
features=watermalon.columns.tolist()[0:-1] #提取特征列表
my_tree=createTree(watermalon_list,features)