【机器学习】朴素贝叶斯、SVM和数据分布检验分析

【机器学习】朴素贝叶斯、SVM和数据分布检验分析

文章目录
1 朴素贝叶斯
2 SVM
    2.1 线性可分
    2.2 最大间隔超平面
    2.3 SVM 最优化问题
3 数据分布检验方法
    3.1 数据分布检验
    3.2 t检验
    3.3 如何检测两组数据是否同分布

1 朴素贝叶斯

朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法，它的核心算法又是什么呢？

是下面这个贝叶斯公式：

换个表达形式就会明朗很多，如下：

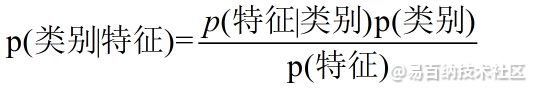
我们最终求的p(类别|特征)即可！就相当于完成了我们的任务。
例题分析
下面我先给出例子问题。

给定数据如下：

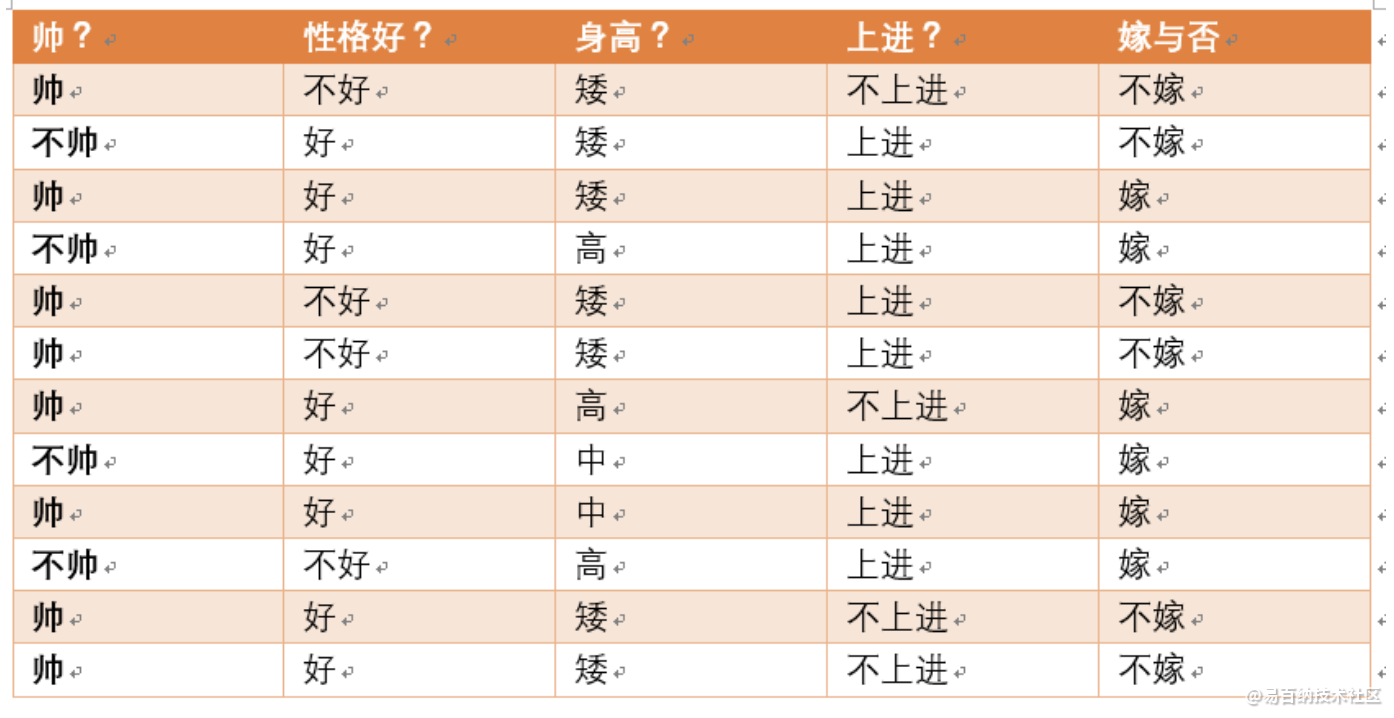
现在给我们的问题是，如果一对男女朋友，男生想女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？

这是一个典型的分类问题，转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率，谁的概率大，我就能给出嫁或者不嫁的答案！

这里我们联系到朴素贝叶斯公式：

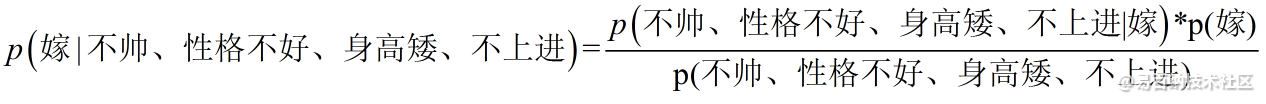
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的，但是通过朴素贝叶斯公式可以转化为好求的三个量，p(不帅、性格不好、身高矮、不上进|嫁)、p（不帅、性格不好、身高矮、不上进)、p(嫁)（至于为什么能求，后面会讲，那么就太好了，将待求的量转化为其它可求的值，这就相当于解决了我们的问题！）

朴素贝叶斯分类的优缺点
优点：

（1） 算法逻辑简单,易于实现

（2）分类过程中时空开销小

缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2 SVM

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

2.1 线性可分

首先我们先来了解下什么是线性可分。

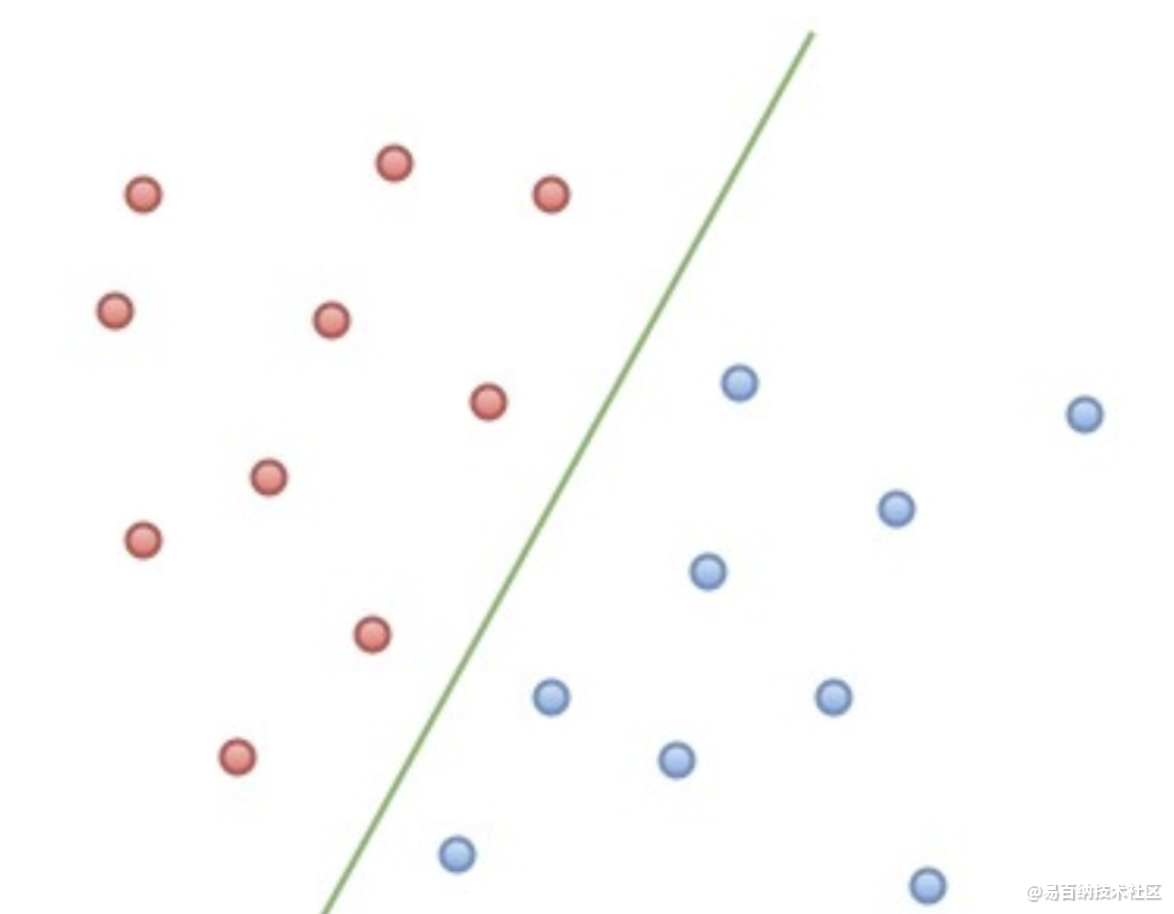
在二维空间上，两类点被一条直线完全分开叫做线性可分。

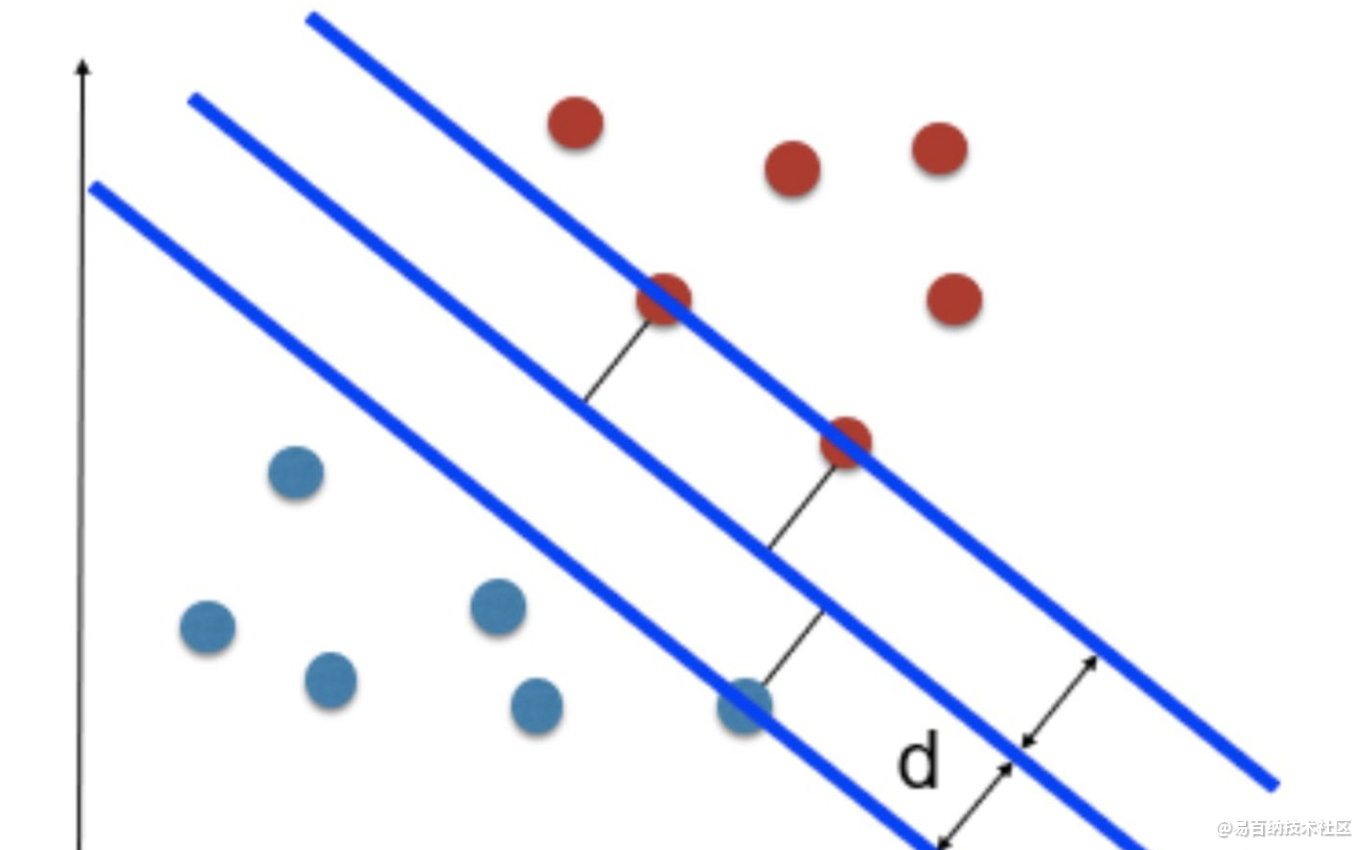
2.2 最大间隔超平面

为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

两类样本分别分割在该超平面的两侧；
两侧距离超平面最近的样本点到超平面的距离被最大化了。

2.3 SVM 最优化问题

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：

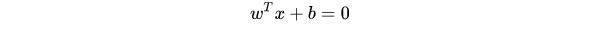
如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。

3 数据分布检验方法

不管是在练习项目还是实际工作中，我们基本上是抽样获取数据，通过一定的抽样设置得到一定数据量，然后从样本数据推断总体分布。但是不同情景下的数据分布是不同的，为了数据分析和后期模型建立，我们需要了解数据的实际分布。

3.1 数据分布检验

1. 判断一组数据是否服从正态分布

 python 
import scipy.stats as stats
 Shapiro-Wilk test, x 为待检测数据，返回统计量和P值,适合样本量小于50
stats.shapiro(x)  

 Kolmogorov–Smirnov,K-S 检验，
 样本量适合50~300，x 待检测数据，cdf为待检验分布，norm可检验正态，返回统计量和P值
stats.kstest (x, cdf, args = ( ), alternative ='two-sided', mode ='approx')stats.anderson (x, dist ='norm' )  # x 为待检测数据，dist为待检测分布，可以正态、指数、二项等
stats.normaltest (a, axis=0) # 样本量大于300

2. 判断两组数据是否服从同一分布-- K-S检验

统计量为各阶段两组数据的累计概率分布差值的最大值

stats.ks_2samp(x, y)

3. 方差齐性检验--F检验

比较两组数据方差是否存在显著性差异，适用于两样本t检验之前。

正态分布 F 检验

p = stats.f.sf(var1, var2, n1-1, n2-1)  

非正态分布

stats.bartlett(*args)  # Bartlett's test 球状检验  ,输入为array_like的sample1,sample2, sample3 ...,返回统计量和P值
stats.levene(*args)   # Levene's test 参数同上，对于显著非正常人群，鲁棒性强

3.2 t检验

t检验（t test）又称学生t检验（Student t-test）可以说是统计推断中非常常见的一种检验方法，用于统计量服从正态分布，但方差未知的情况。

有关t检验的历史（以及学生t检验的由来）可以参考维基百科。

t检验的前提是要求样本服从正态分布或近似正态分布，不然可以利用一些变换（取对数、开根号、倒数等等）试图将其转化为服从正态分布是数据，如若还是不满足正态分布，只能利用非参数检验方法。不过当样本量大于30的时候，可以认为数据近似正态分布。

t检验最常见的四个用途：

单样本均值检验（One-sample t-test）
用于检验 总体方差未知、正态数据或近似正态的 单样本的均值 是否与 已知的总体均值相等
两独立样本均值检验（Independent two-sample t-test）
用于检验 两对独立的 正态数据或近似正态的 样本的均值 是否相等，这里可根据总体方差是否相等分类讨论
配对样本均值检验（Dependent t-test for paired samples）
用于检验 一对配对样本的均值的差 是否等于某一个值
回归系数的显著性检验（t-test for regression coefficient significance）
用于检验 回归模型的解释变量对被解释变量是否有显著影响

3.3 如何检测两组数据是否同分布

一个模型中，很重要的技巧就是要确定训练集与测试集特征是否同分布，这也是机器学习的一个很重要的假设，但很多时候我们默认这个道理，却很难有方法来保证数据同分布。

T检验是一种适合小样本的统计分析方法，通过比较不同数据的均值，研究两组数据是否存在差异。

单样本t检验
单样本t检验是样本均值与总体均值的比较问题。其中总体服从正态分布，从正态总体中抽样得到n个个体组成抽样样本，计算抽样样本均值和标准差，判断总体均值与抽样样本均值是否相同。

from scipy.stats import ttest_1samp
import numpy as np

print("Null Hypothesis:μ=μ0=30，α=0.05")
ages = [25,36,15,40,28,31,32,30,29,28,27,33,35]
t = (np.mean(ages)-30)/(np.std(ages,ddof=1)/np.sqrt(len(ages)))

ttest,pval = ttest_1samp(ages,30)
print(t,ttest)
if pval < 0.05:
    print("Reject the Null Hypothesis.")
else:
    print("Accept the Null Hypothesis.")