机器学习（三）：使用更复杂的回归模型进行房价预测_专栏

在上一篇文章中，我们介绍了如何使用线性回归模型进行房价预测。我们发现虽然结果能够预测数据的走向，但是并不能很好地贴合数据。因此我们将尝试使用更加复杂的模型对数据进行预测，观察预测结果并尝试分析并解决随之而来的诸多问题。

一、使用二次模型进行预测

线性回归模型中，我们用来拟合数据的函数模型为直线函数，格式为y=ax+b，该模型一共有两个参数a，b。二次模型中，拟合的函数模型为y=ax^2+bx+c，一共有三个参数a，b，c。同样，损失函数定义为：

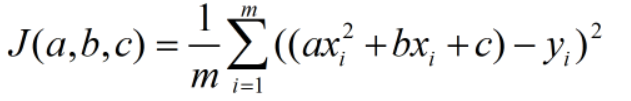
损失函数对三个参数的偏导数为：

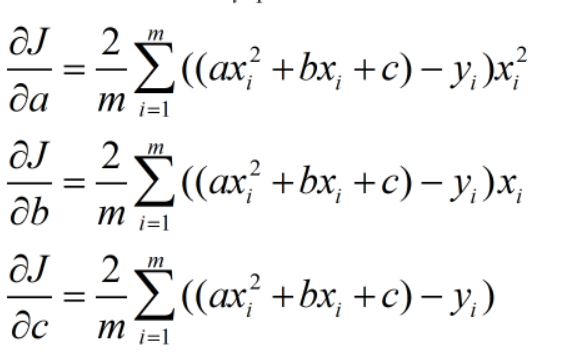
具体编程实现如下：
导入数据集并进行处理：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 导入数据
datasFile=pd.read_csv('data/data1810/data.txt',names=['size','price'])
datas=np.array(datasFile)
# 划分数据集
trainSet=datas[0:600,:]
testSet=datas[600:,:]

trainX=trainSet[:,0]
trainY=trainSet[:,1]

testX=testSet[:,0]
testY=testSet[:,1]

# 归一化数据，最大最小值按照训练数据集来取
trainX_min_max=(trainX-np.min(trainX))/(np.max(trainX)-np.min(trainX));
trainY_min_max=(trainY-np.min(trainY))/(np.max(trainY)-np.min(trainY));

testX_min_max=(testX-np.min(testX))/(np.max(testX)-np.min(testX));
testY_min_max=(testY-np.min(testY))/(np.max(testY)-np.min(testY));

使用回归模型进行训练，注意，回归模型为二次模型：

import random
# 初始化回归相关参数值
a=random.random()# 随机初始化一个值
b=random.random()
c=random.random()

x=trainX_min_max
y=trainY_min_max

lr=0.05# 学习率
iter=1000 # 训练次数
# 开始训练
for i in range(iter):
    predict=a*x*x+b*x+c # 使用二次函数预测
    # 计算损失函数
    J=np.mean((predict-y)*(predict-y))
    # 计算损失函数的梯度值
    J_grad_a=np.mean((predict-y)*x*x)
    J_grad_b=np.mean((predict-y)*x)
    J_grad_c=np.mean(predict-y)
    # 进行参数迭代
    a=a-lr*J_grad_a
    b=b-lr*J_grad_b
    c=c-lr*J_grad_c
    # 打印参数的值
    print("iter=%d," % i)
    print("cost=%.3f" % J)
    print("a=%.3f," % a)
    print("b=%.3f," % b)
    print("c=%.3f," % c)
    print("\n")

训练结果如图：

结果可视化：

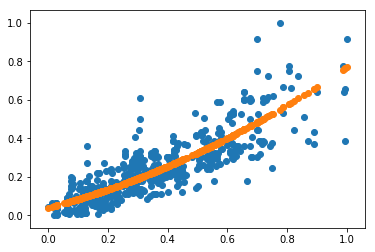
用训练好的模型进行预测：

# 进行预测
x=testX_min_max
y=testY_min_max
result=a*x*x+b*x+c
# 计算预测误差
err=np.mean((result-y)*(result-y))
# 打印误差
print('err=%.3f' % err)
# 绘制拟合结果
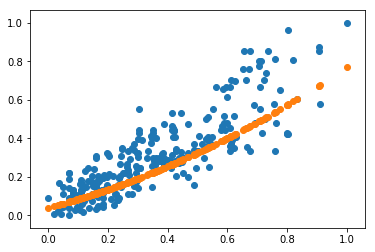
plt.scatter(x,y)
plt.scatter(x,result)

误差为：

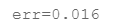
结果可视化：

相关完整代码如下：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random
# 导入数据
datasFile=pd.read_csv('data/data1810/data.txt',names=['size','price'])
datas=np.array(datasFile)
# 划分数据集
trainSet=datas[0:600,:]
testSet=datas[600:,:]

trainX=trainSet[:,0]
trainY=trainSet[:,1]

testX=testSet[:,0]
testY=testSet[:,1]

# 归一化数据，最大最小值按照训练数据集来取
trainX_min_max=(trainX-np.min(trainX))/(np.max(trainX)-np.min(trainX));
trainY_min_max=(trainY-np.min(trainY))/(np.max(trainY)-np.min(trainY));

testX_min_max=(testX-np.min(testX))/(np.max(testX)-np.min(testX));
testY_min_max=(testY-np.min(testY))/(np.max(testY)-np.min(testY));
import random
# 初始化回归相关参数值
a=random.random()# 随机初始化一个值
b=random.random()
c=random.random()

x=trainX_min_max
y=trainY_min_max

lr=0.05# 学习率
iter=1000 # 训练次数
# 开始训练
for i in range(iter):
    predict=a*x*x+b*x+c # 使用二次函数预测
    # 计算损失函数
    J=np.mean((predict-y)*(predict-y))
    # 计算损失函数的梯度值
    J_grad_a=np.mean((predict-y)*x*x)
    J_grad_b=np.mean((predict-y)*x)
    J_grad_c=np.mean(predict-y)
    # 进行参数迭代
    a=a-lr*J_grad_a
    b=b-lr*J_grad_b
    c=c-lr*J_grad_c
    # 打印参数的值
    print("iter=%d," % i)
    print("cost=%.3f" % J)
    print("a=%.3f," % a)
    print("b=%.3f," % b)
    print("c=%.3f," % c)
    print("\n")
# 结果可视化
plt.scatter(trainX_min_max,trainY_min_max)
plt.scatter(trainX_min_max,predict)
# 进行预测
x=testX_min_max
y=testY_min_max
result=a*x*x+b*x+c
# 计算预测误差
err=np.mean((result-y)*(result-y))
# 打印误差
print('err=%.3f' % err)
# 绘制拟合结果
plt.scatter(x,y)
plt.scatter(x,result)

我们发现，使用二次模型时训练数据的误差没有发生改变，但是测试集的误差有所降低。可见，采用更复杂的模型的确能够更精准地预测数据。