机器学习之回归

一、前言

  什么是机器学习？机器学习的本质就是函数的拟合，也就是我们这篇文章的主题——拟合。举个例子，比如人脸识别就是拟合出这样一个函数：输入为人脸图片，输出为这张脸的主人；又或者是语音识别的目标是拟合出这样一个函数：输入为一条语音，输出为这条语音所含的信息。本篇文章，将考虑最简单的一元线性回归的情况，为大家介绍一下处理回归问题的基本方法。

二、损失函数

  我们需要用一个函数来衡量机器的输出与真实情况之间的误差，这个函数就称为损失函数。在本文，我们将误差函数J定义为每个预测值与实际值误差平方和的平均值。在输入输出关系确定的情况下，对于给定的一个输入，那么我们对于这个输入数据的预测值就能唯一确定，预测值与真实值之间的误差也就唯一确定，即损失函数能够唯一确定，我们需要做的就是改变当前的函数关系，使得损失函数的值减小。那么，如何降低损失函数呢？这就是机器学习任务的一个难点。

三、梯度下降法

  在机器学习任务中，我们采用梯度下降法来降低损失函数的值。为了便于读者理解，我们首先考虑损失函数为一元可导函数的情况，此时，设损失函数为J(a)。我们知道，在处处可导的一段一元函数曲线上，极小值的导数必定为零；单调增加的区域上，导数必定大于零；单调减小的区域上，导数必定小于零。利用这个原理，我们可以计算损失函数J(a)在当前状态的导数值，若导数值大于0，说明损失函数处于单调增加的情况，则需要减小自变量a；若导数值小于0，说明损失函数处于单调减小的情况，此时需要增大自变量a；若导数等于0，则a的值不变，此时损失函数处于极小值（局部最小值）。以上过程可以用图示法更为清晰地表示出来。
  导数的几何意义便是曲线上某个点的切线，导数值便是切线的斜率。如图，A点的位置代表当前的状态。我们做出a点处的切线，观察切线的斜率。当A点在极小值的左边时，切线斜率小于0，我们需要将A点右移，即增大自变量a的值：

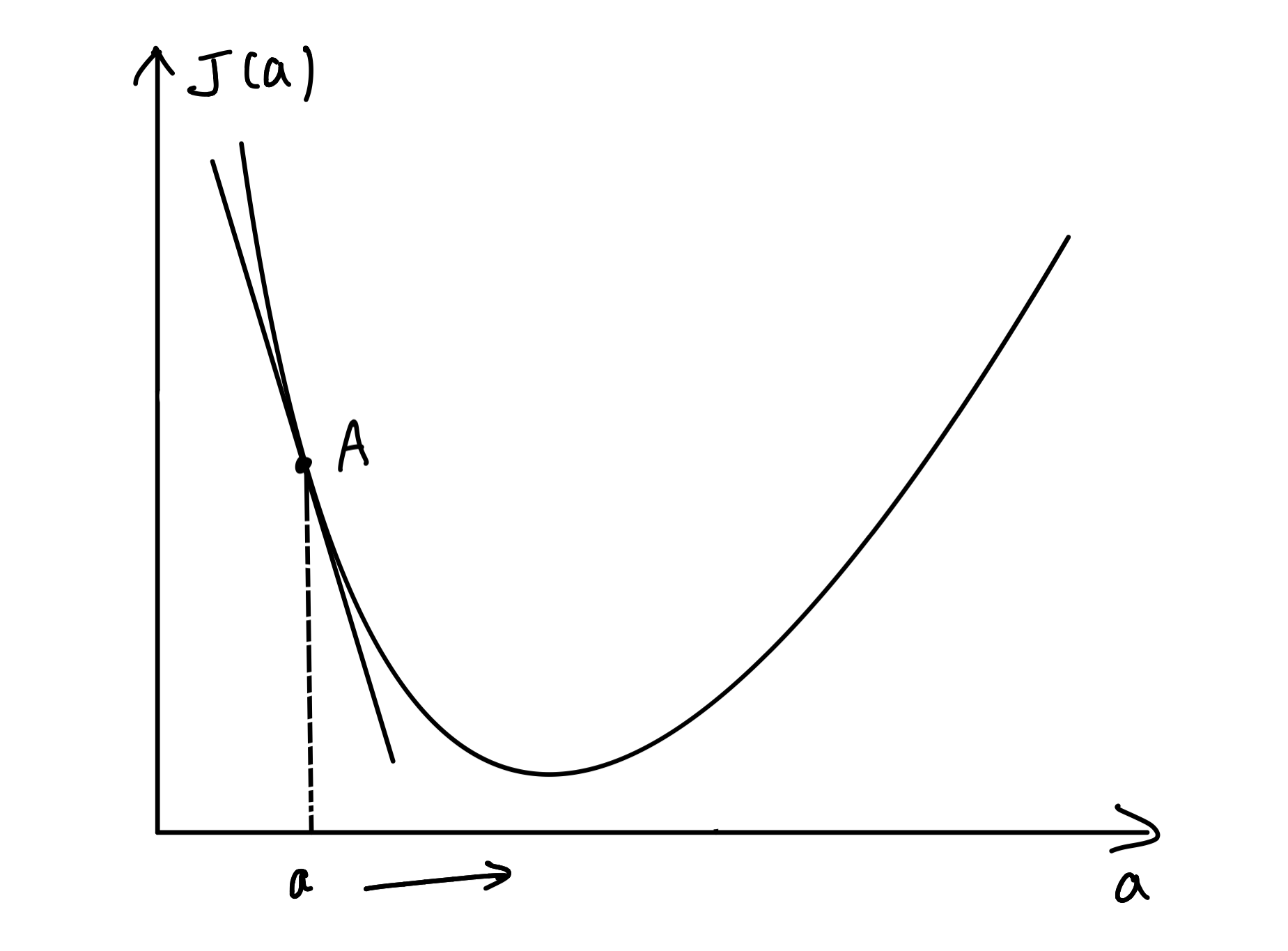
当A点在极小值右边时，切线斜率则大于0，我们需要将A点左移，即减小自变量a的值：

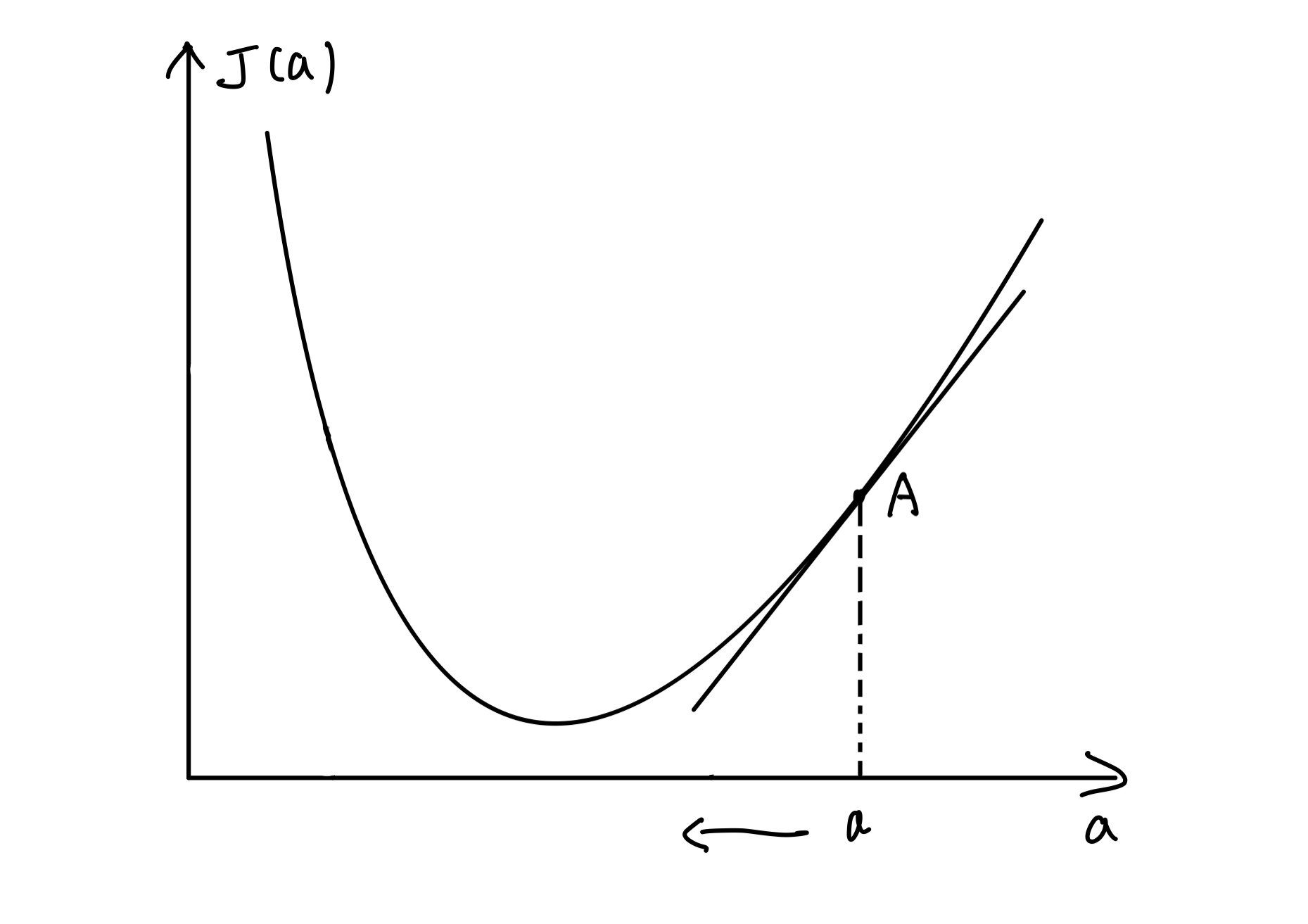
我们把每一步自变量a的更新过程抽象为以下公式：

其中，n为大于0的值，决定着每一步自变量更新的步长。可以看出，当导数值大于0时，a值减小；当导数值小于0时，a值增大，最终a值会稳定在导数值为0的点，也就是极小值点。
  本文的主题为一元线性回归，即输入输出的关系为一元线性函数，在几何上表示为一条直线。我们知道，直线方程一般由两个参数决定：斜率a和截距b，方程可以表示为y=ax+b。则损失函数定义为：

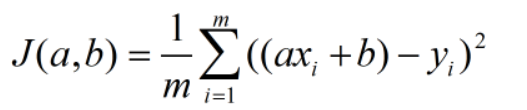
当参数值不唯一时，我们需要计算损失函数对于每个参数的偏导值，然后和单变量的处理方法一样，分别更新每一个参数，我们可以将此过程抽象为以下公式：

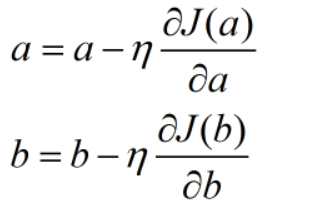
其中，利用导数运算公式，损失函数对参数a，b的偏导数分别表示为：

以上式中，m为样本数量。

四、一元线性回归的编程实现

  下面，我们将用python对梯度下降法进行一个简单的实现，以演示机器学习算法工作的过程。首先，我们准备一个数据集，该数据集上的每一个点都来自某一条直线，该直线的参数我们不会事先告知，让我们一起来看看梯度下降法加持下的机器能否拟合出这条直线呢？
  首先我们制作一个数据集，该数据集中的数据点均在直线y=2x+3上，我们来看一下我们通过梯度下降法你和出来的关系式是否为y=2x+3.部分数据集信息如下图：

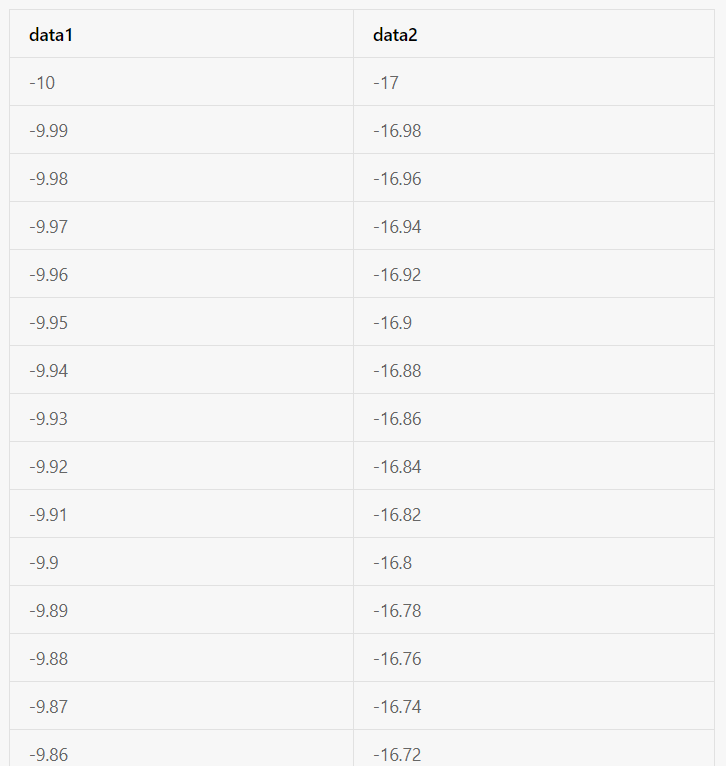
编程实现如下：
  首先我们导入数据集：

import pandas as pd
import numpy as np

datas=pd.read_csv('data/data71150/data.csv')# 读取数据集
datas=np.array(datas)# 将数据转换为np数组的形式
# 提取x和y值，本次回归任务的目的，就是拟合出x与y的关系式。
x=datas[:,0]
y=datas[:,1]

  然后初始化我们需要拟合的参数。在线性回归任务中，损失函数仅有一个极小值，因此我们可以使用任何方法对参数进行初始化。但在其他的回归任务中，损失函数存在多个极小值，算法会收敛到局部最优点，初始化参数的方法直接影响着我们的回归结果。我们在本次任务中直接将参数初始化为0即可：

# 初始化参数a，b
a=0
b=0

  设置迭代次数iter以及学习率lr，lr也就是之前我们迭代公式中的η。接着开始迭代，代码如下：

iter=1000;# 迭代次数设为1000
lr=0.01;#学习率
for i in range(iter):
    # 计算损失函数
    J=np.mean(((a*x+b)-y)*((a*x+b)-y))
    # 计算损失函数的梯度值
    J_grad_a=np.mean(((a*x+b)-y)*x)
    J_grad_b=np.mean((a*x+b)-y)
    # 进行参数迭代
    a=a-lr*J_grad_a
    b=b-lr*J_grad_b
    # 打印参数的值
    print("iter=%d," % i)
    print("cost=%.3f" % J)
    print("a=%.3f," % a)
    print("b=%.3f," % b)
    print("\n")

迭代过程中我们打印每一个状态的参数值以及损失函数值，部分结果如下图：


可以看到，最终算法收敛时，参数a为2，b为3。符合我们之前设定的关系是y=2*x+3.并且损失函数值最终降为0，我们的梯度下降法运行得十分完美。

五、总结

  一元线性回归是机器学习任务中最简单的情况，但又是机器学习算法的基础。我们在此基础上，还可以通过更改学习率从而降低迭代次数，使得算法更快地收敛。此外，对于其他回归任务，损失函数不止一个极小值，这就意味着我们的算法很有可能会收敛到某一个极小值（局部最优解）而不是全局的最小值，因此，我们还需在此基础上进一步地优化算法。