模式识别之数据降维（一）：使用遗传算法进行特征提取_专栏

一、前言

在之前的文章中，我们已经接触了一些分类器，在使用这些分类器的时候，我们直接将数据集作为输入，虽然能够达到不错的分类效果，但是程序耗时普遍较高，尤其是多分类任务。毕竟我们使用的数据集维数为190，也就是说我们的数据集中每个数据都有190个特征。聪明的读者可能会想，这190个特征缺一不可吗？我们能不能只使用其中的个别特征就实现性能不错的分类器呢？答案当然是可以，本篇文章开始，我们将介绍数据降维的方法。
数据降维可以分为两个大类：特征选择和特征提取。特征选择是直接选择对分类有用的特征，放弃其他的特征，以降低数据的维度。特征提取是将数据进行一定的变换，比如前面所讲的fisher线性判别，我们可以使用类似投影的方法，将高维数据变换到低维，以实现数据降维。我们先从特征选择开始介绍。本篇文章，我们将为大家介绍其中一种特征选择的方法，即使用遗传算法进行特征选择。关于遗传算法，我在另一个系列的文章中专门介绍过，感兴趣的读者可以自行查阅。

二、matlab实现

使用遗传算法进行特征选择。经过20轮选择、交叉、变异的过程，选出最优的40个维度的特征。适应度设为bayes分类器的正确率。
相关代码如下：

（1）读取数据集并产生初始化种群

（2）经过20轮迭代，每轮进行一次选择、交叉、变异过程

（3）在最后一轮迭代生成的50个个体中，选出最优的一个，作为最终特征选择的结果

（4）初始化种群的函数

（5）选择过程函数。使用赌轮算法，适应度越大的个体越容易被选中

（6）交叉过程函数

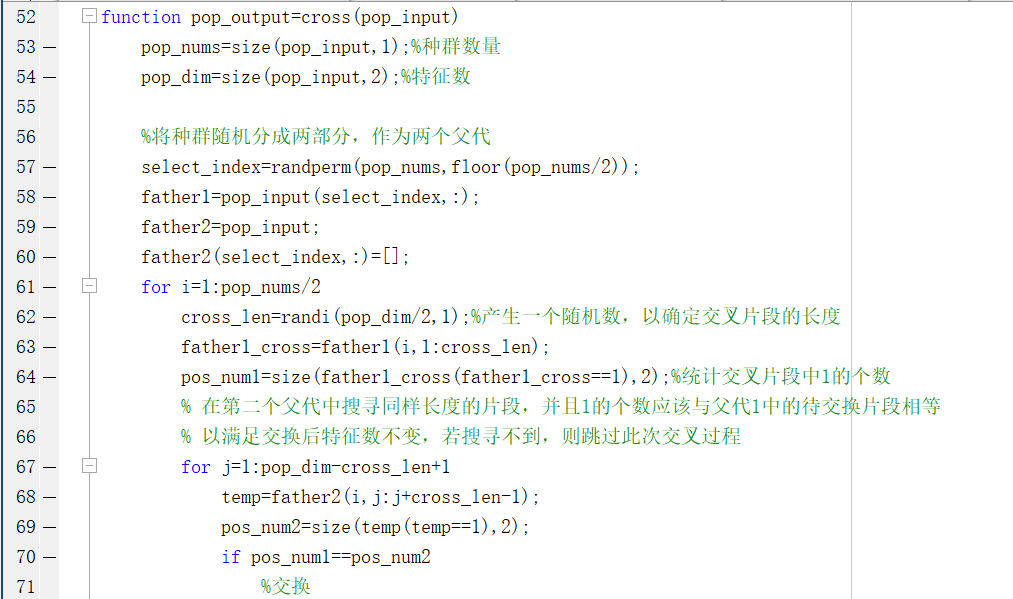
（7）变异过程

（8）适应度函数。即贝叶斯分类过程，分类的正确率作为输出的适应度

完整代码如下：

%使用遗传算法进行特征选择，学习算法采用贝叶斯
clear
load('2-Class Problem.mat');
tic
% 产生初始化种群，其中含有50个个体，一个个体含有190个维度，最终选择出40个最优的维度
pop_init=pop_init_genrator(50,190,40);
pop_last=pop_init;
% 开始迭代
for iter=1:20
    fprintf('开始第%d次迭代\n',iter);
    pop_new=pop_select(pop_last,Training_class1,Training_class2,Testing,Label_Testing);%选择
    pop_new=cross(pop_new);%交叉
    pop_new=variation(pop_new);%变异
    pop_last=pop_new;
end
pop_selected=pop_last;
%计算适应度，选择最优的个体，即选出最终的特征
% fit=fitness_jd(pop_selected,Training_class1,Training_class2);
fit=fitness_bayes(pop_selected,Training_class1,Training_class2,Testing,Label_Testing);
fit_sort=sort(fit);
best_pop=pop_selected(fit==fit_sort(end),:);
feature_selected=find(best_pop==1);
save('feature_selected_GA','feature_selected');
toc
% 产生初始种群的函数 pop_nums:种群数量 precision:精度，这里指特征的总数量 
% positive：一个个体中‘1’的个数，这里指最终选择40个特征
function pop_init=pop_init_genrator(pop_nums,precision,positive)
    pop_init=zeros(pop_nums,precision);
    for i=1:pop_nums
        pop_init(i,:)=randerr(1,precision,positive);
    end
end
% 选择，使用赌轮算法
function pop_new=pop_select(pop_last,train_class1,train_class2,Testing,Label_Testing)
    disk=0;%初始化轮盘
%     fit=fitness_jd(pop_last,train_class1,train_class2);%计算上一代每个个体的适应度
    fit=fitness_bayes(pop_last,train_class1,train_class2,Testing,Label_Testing);
    pop_nums=size(fit,2);
%     定义轮盘，每一个个体的区域正比于个体的适应度，个体适应度越高，被选中的概率越大
    for i=1:pop_nums
        disk(i)=sum(fit(1:i));
    end
    rand_=max(fit)*rand(1,pop_nums);%产生一组随机数，随机数的个数等于种群的个体数
    %选择
    for i=1:pop_nums
        temp=find(disk<rand_(i));
        index=size(temp,2)+1;%找到随机数落在轮盘的位置
        pop_new(i,:)=pop_last(index,:);
    end
end
%交叉
function pop_output=cross(pop_input)
    pop_nums=size(pop_input,1);%种群数量
    pop_dim=size(pop_input,2);%特征数

    %将种群随机分成两部分，作为两个父代
    select_index=randperm(pop_nums,floor(pop_nums/2));
    father1=pop_input(select_index,:);
    father2=pop_input;
    father2(select_index,:)=[];
    for i=1:pop_nums/2
        cross_len=randi(pop_dim/2,1);%产生一个随机数，以确定交叉片段的长度
        father1_cross=father1(i,1:cross_len);
        pos_num1=size(father1_cross(father1_cross==1),2);%统计交叉片段中1的个数
        % 在第二个父代中搜寻同样长度的片段，并且1的个数应该与父代1中的待交换片段相等
        % 以满足交换后特征数不变，若搜寻不到，则跳过此次交叉过程
        for j=1:pop_dim-cross_len+1
            temp=father2(i,j:j+cross_len-1);
            pos_num2=size(temp(temp==1),2);
            if pos_num1==pos_num2
                %交换
                father1(i,1:cross_len)=temp;
                father2(i,j:j+cross_len-1)=father1_cross;
                break;
            end
        end
    end
    pop_output=[father1;father2];
end
%变异
function pop_output=variation(pop_input)
    pop_nums=size(pop_input,1);%种群数量
    pop_dim=size(pop_input,2);%特征数
    prob=rand(1,pop_nums);%产生一组随机数，决定是否变异的概率，大于0.5则变异
    for i=1:pop_nums
        if prob(i)<0.5
            continue;
        else
            %产生两个个随机数，确定变异的位置，为确保变异后特征数不变，需要变异的两个位置值不能相等
            index1=randi(pop_dim,1);
            index2=randi(pop_dim,1);
            while pop_input(i,index1)==pop_input(i,index2)
                index2=randi(pop_dim,1);
            end
            pop_input(i,index1)=~pop_input(i,index1);
            pop_input(i,index2)=~pop_input(i,index2);
        end
    end
    pop_output=pop_input;
end
% 适应度函数,选择类间距离，距离度量采用欧氏距离
function fit=fitness_jd(pop,train_class1,train_class2)
    pop_num=size(pop,1);
    class1_num=size(train_class1,2);
    class2_num=size(train_class2,2);
    for i=1:pop_num
        d=0;
        for j=1:class1_num
            for k=1:class2_num
                d=d+(train_class1(pop(i,:)==1,j)-train_class2(pop(i,:)==1,k))'*(train_class1(pop(i,:)==1,j)-train_class2(pop(i,:)==1,k));
            end
        end
        jd=d/(class1_num*class2_num);
        fit(i)=jd;
    end
end    
%贝叶斯算法的准确度作为可分性依据
function fit=fitness_bayes(pop,Training_class1,Training_class2,testing_data,Testing_label)
    pop_num=size(pop,1);
    %获取训练数量
    n1=size(Training_class1,2);
    n2=size(Training_class1,2);
    % 先验概率
    pw1=n1/(n1+n2);
    pw2=n2/(n1+n2);
    for p=1:pop_num
        %选择训练数据和测试数据相应位置的特征值
        Training_data1=Training_class1(pop(p,:)==1,:);
        Training_data2=Training_class2(pop(p,:)==1,:);
        Testing_data=testing_data(pop(p,:)==1,:);
        %参数估计
        [miu1,sigma1]=ParamerEstimation(Training_data1);
        [miu2,sigma2]=ParamerEstimation(Training_data2);
        %预测结果
        predict_label=0;
        test_num=size(Testing_data,2);%获取测试数据数量
        for i=1:test_num
            x=Testing_data(:,i);
            pxw1=gaussian(miu1,sigma1,x);
            pxw2=gaussian(miu2,sigma2,x);
            if pw1*pxw1>pw2*pxw2
                predict_label(i)=1;
            else
                predict_label(i)=2;
            end
        end
        % 计算精度
        acc=sum(predict_label==Testing_label)/test_num;
    end
    fit(p)=acc;
end

程序运行结果：

遗传算法经过20次迭代，最终选出最优的40个特征。