线性分类器与非线性分类器（二）：Fisher线性判别_专栏

一、什么是Fisher判别

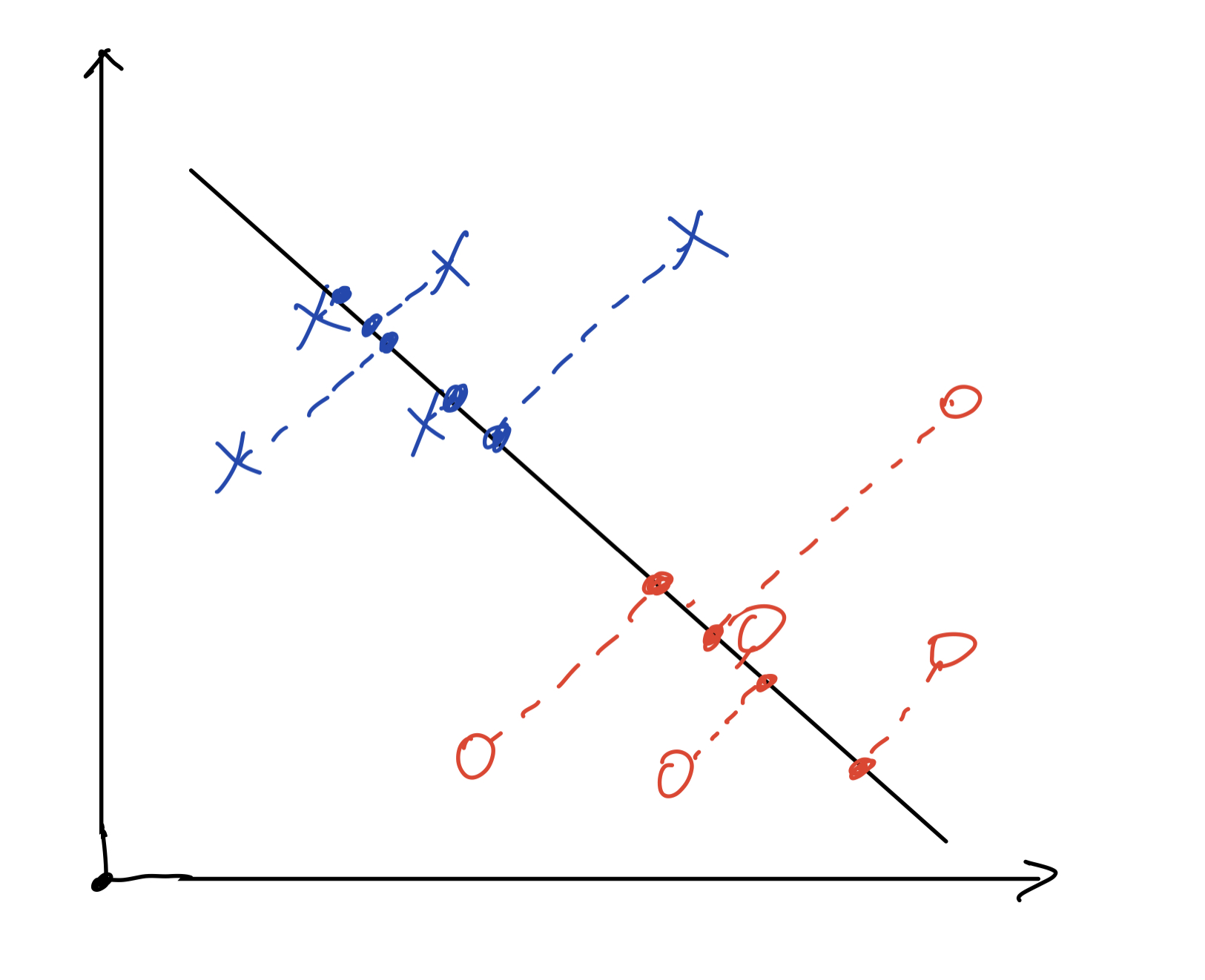
Fisher线性判别给模式识别问题提供了一个新思路，与Bayes决策以及其他的决策方法直接处理高维问题不同，Fisher线性判别是将d维数据投影到1维空间进行分类。因此，使用Fisher线性判别进行分类就可以归结为寻找最佳投影方向的问题，在这个最佳投影方向上，样本的投影能够分开得最好。
如图，将二维平面中的数据投影到一条直线上之后，分类问题就简单很多，我们只需要找到一个点作为分类边界即可。

二、Fisher线性判别的Matlab实现

Fisher线性判别要解决的基本问题就是确定最佳投影方向。要确定最佳的投影方向，首先得计算出类内离散度和各类样本的均值，然后通过相应公式即可计算出最佳投影距离。最后确定一维空间的分类阈值，从而对样本进行分类。分类阈值的确定有三种方法——均值中点法、类样本数加权法和先验概率加权法。
具体Matlab实现如下：
（1）导入数据，获取相关信息，并计算各类样本的均值。flag变量用于选择分类阈值的确定方法。

clear
load('2-Class Problem.mat')
flag=3;% 1:均值中点法。2:类样本数加权法。3:先验概率加权法
tic
% 获取数据集信息
[d1,n1]=size(Training_class1);
[d2,n2]=size(Training_class2);
test_num=size(Testing,2);
% 各类样本均值
m1=sum(Training_class1,2)/n1;
m2=sum(Training_class2,2)/n2;

（2）计算类内离散度，计算最佳投影方向并将数据投影到一维空间

% 计算类内离散度
s1=(Training_class1-m1)*(Training_class1-m1)';
s2=(Training_class2-m2)*(Training_class2-m2)';
% 最佳投影方向
w=(s1+s2)\(m1-m2);
% 将数据投影到一维Y空间
y1=w'*Training_class1;
m1_=sum(y1)/n1;
y2=w'*Training_class2;
m2_=sum(y2)/n2;
y=w'*Testing;

（3）确定分类阈值并进行分类
a.使用均值中点法：

% 预测
if flag==1
    % 使用均值中点法确定分类阈值
    y01=(m1_+m2_)/2;
    predict=0;
    for i=1:test_num
        if y(i)>y01
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用均值中点法，准确度为：%.2f%%\n',acc*100);

b.使用类样本数加权法：

elseif flag==2
    % 使用类样本数加权法
    y02=(n1*m1_+n2*m2_)/(n1+n2);
    predict=0;
    for i=1:test_num
        if y(i)>y02
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用类样本数加权法，准确度为：%.2f%%\n',acc*100);

c.使用先验概率加权法：

else
    % 使用先验概率加权法
    pw1=n1/(n1+n2);
    pw2=n2/(n1+n2);
    y03=(m1_+m2_)/2+(log(pw1)-log(pw2))/(n1+n2-2);
    predict=0;
    for i=1:test_num
        if y(i)>y03
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用先验概率加权法，准确度为：%.2f%%\n',acc*100);
end
toc

完整代码如下：

clear
load('2-Class Problem.mat')
flag=3;% 1:均值中点法。2:类样本数加权法。3:先验概率加权法
tic
% 获取数据集信息
[d1,n1]=size(Training_class1);
[d2,n2]=size(Training_class2);
test_num=size(Testing,2);
% 各类样本均值
m1=sum(Training_class1,2)/n1;
m2=sum(Training_class2,2)/n2;
% 计算类内离散度
s1=(Training_class1-m1)*(Training_class1-m1)';
s2=(Training_class2-m2)*(Training_class2-m2)';
% 最佳投影方向
w=(s1+s2)\(m1-m2);
% 将数据投影到一维Y空间
y1=w'*Training_class1;
m1_=sum(y1)/n1;
y2=w'*Training_class2;
m2_=sum(y2)/n2;
y=w'*Testing;
% 预测
if flag==1
    % 使用均值中点法确定分类阈值
    y01=(m1_+m2_)/2;
    predict=0;
    for i=1:test_num
        if y(i)>y01
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用均值中点法，准确度为：%.2f%%\n',acc*100);
elseif flag==2
    % 使用类样本数加权法
    y02=(n1*m1_+n2*m2_)/(n1+n2);
    predict=0;
    for i=1:test_num
        if y(i)>y02
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用类样本数加权法，准确度为：%.2f%%\n',acc*100);
else
    % 使用先验概率加权法
    pw1=n1/(n1+n2);
    pw2=n2/(n1+n2);
    y03=(m1_+m2_)/2+(log(pw1)-log(pw2))/(n1+n2-2);
    predict=0;
    for i=1:test_num
        if y(i)>y03
            predict(i)=1;
        else
            predict(i)=2;
        end
    end
    acc=sum(predict==Label_Testing)/test_num;
    fprintf('使用先验概率加权法，准确度为：%.2f%%\n',acc*100);
end
toc

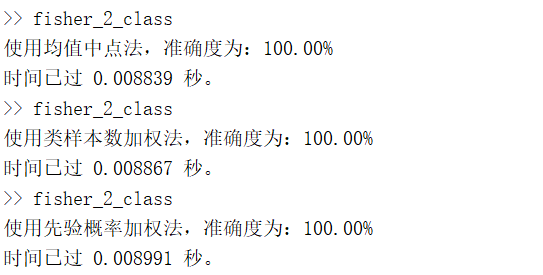
运行结果分析:Fisher线性判别处理二分类问题时，运行时长都在0.01s以内，而且三种分类阈值确定方法均可达到100%的分类正确率。