贝叶斯多分类实现之非参数估计方法

一、前言

  在之前的文章中，我们已经实现了使用参数估计类的条件概率密度来进行多分类，这篇文章，我将继续使用非参数估计方法，并与参数估计方法的效果进行对比，以及对之前所有的算法进行一个性能方面的总结。本篇将是这个系列最后一篇文章。

二、使用非参数估计方法进行多分类

  与参数估计方法类似，只不过在估计类的条件概率密度时使用相应的非参数估计方法。此外，还需要对数据进行适当缩放，防止运算溢出。

a. Parzen窗法（h=0.75）

相关代码如下：
导入数据、获取数据信息并对数据进行缩放处理。

clear
warning off;
load('Mult-class Problem.mat');

tic
%数据缩放，防止溢出
Testing_data=Testing_data/100;
Training_data=Training_data/100;
% 获取数据集信息
class_nums=Label_training(end);% 类别数
test_nums=size(Testing_data,2);% 测试样本数量
train_nums=size(Training_data,2);    %训练样本数量

计算先验概率。

% 计算先验概率
for class=1:class_nums
    Training_temp=Training_data(:,Label_training==class);
    num=size(Training_temp,2);
    pw(class)=num/train_nums;
end

遍历测试样本，对样本进行分类，打印实时正确率

for i=1:test_nums
    for class=1:class_nums
        x=Testing_data(:,i);
        Training_temp=Training_data(:,Label_training==class);
        g(class)=pw(class)*Parzen(x,0.75,Training_temp);
    end
    [~,argmax]=max(g);
    predict(i)=argmax;
    if mod(i,100) == 0
        acc=sum(predict==Label_testing(1:i))/i;
        disp(['预测数据号：' num2str(i)])
        disp(['准确度是：' num2str(acc)])
    end
end

计算总正确率

acc=sum(predict==Label_testing(1:test_nums))/test_nums;        
toc
disp(['总准确度是：' num2str(acc)])

完整代码如下：

clear
warning off;
load('Mult-class Problem.mat');

tic
%数据缩放，防止溢出
Testing_data=Testing_data/100;
Training_data=Training_data/100;
% 获取数据集信息
class_nums=Label_training(end);% 类别数
test_nums=size(Testing_data,2);% 测试样本数量
train_nums=size(Training_data,2);    %训练样本数量

predict=0;
% 计算先验概率
for class=1:class_nums
    Training_temp=Training_data(:,Label_training==class);
    num=size(Training_temp,2);
    pw(class)=num/train_nums;
end

for i=1:test_nums
    for class=1:class_nums
        x=Testing_data(:,i);
        Training_temp=Training_data(:,Label_training==class);
        g(class)=pw(class)*Parzen(x,0.75,Training_temp);
    end
    [~,argmax]=max(g);
    predict(i)=argmax;
    if mod(i,100) == 0
        acc=sum(predict==Label_testing(1:i))/i;
        disp(['预测数据号：' num2str(i)])
        disp(['准确度是：' num2str(acc)])
    end
end

acc=sum(predict==Label_testing(1:test_nums))/test_nums;        
toc
disp(['总准确度是：' num2str(acc)])

程序运行结果分析：运行耗时大约是参数估计方法的一半，但正确率没有使用参数估计方法高，仅为65%。

b.Kn近邻法（N=2）

编程实现与Parzen窗法类似，只是类的条件概率密度使用近邻法进行估计。

for i=1:test_nums
    for class=1:class_nums
        x=Testing_data(:,i);
        Training_temp=Training_data(:,Label_training==class);
        g(class)=pw(class)*KNN(x,2,Training_temp);
    end
    [~,argmax]=max(g);
    predict(i)=argmax;
    if mod(i,100) == 0
        acc=sum(predict==Label_testing(1:i))/i;
        disp(['预测数据号：' num2str(i)])
        disp(['准确度是：' num2str(acc)])
    end
end

完整代码如下：

clear
warning off;
load('Mult-class Problem.mat');

tic
%数据缩放，防止溢出
Testing_data=Testing_data/100;
Training_data=Training_data/100;
% 获取数据集信息
class_nums=Label_training(end);
test_nums=size(Testing_data,2);
train_nums=size(Training_data,2);    

predict=0;
% 计算先验概率
for class=1:class_nums
    Training_temp=Training_data(:,Label_training==class);
    num=size(Training_temp,2);
    pw(class)=num/train_nums;
end

for i=1:test_nums
    for class=1:class_nums
        x=Testing_data(:,i);
        Training_temp=Training_data(:,Label_training==class);
        g(class)=pw(class)*KNN(x,2,Training_temp);
    end
    [~,argmax]=max(g);
    predict(i)=argmax;
    if mod(i,100) == 0
        acc=sum(predict==Label_testing(1:i))/i;
        disp(['预测数据号：' num2str(i)])
        disp(['准确度是：' num2str(acc)])
    end
end

acc=sum(predict==Label_testing(1:test_nums))/test_nums;        
toc
disp(['总准确度是：' num2str(acc)])

运行结果分析：使用Kn近邻法时，程序运行效率略高于Parzen窗法，但分类性能较差。

三、各种算法性能对比

  到此，所有关于最小错误贝叶斯决策方法都已经为大家实现了，大家可以照着例子自行练习。所有实现的代码性能对比如下表：

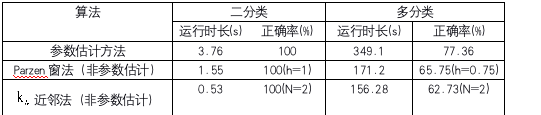
  我们可以看出，非参数估计方法可以大大降低程序的耗时，不论是二分类还是多分类任务。但是从多分类任务来看，非参数估计的分类正确率不如参数估计。也就是说，非参数估计概率密度的方法不一定比参数估计优越。

四、总结与反思

  使用最小错误率的贝叶斯决策可以得到十分不错的性能——二分类100%的正确率和多分类最高77%的正确率，此外，贝叶斯决策是基于概率统计的决策方法，具有很好的可解释性，但是原理较为复杂，要理解贝叶斯决策方法，需要具备许多概率统计相关知识。目前看来，使用贝叶斯决策还有一个问题，即程序运行耗时长，效率不高——二分类参数估计方法大约耗时4s，非参数估计方法大约耗时1.5s，多分类参数估计方法大约耗时6min，非参数估计方法大约耗时3min。当然，这也可能与数据维数太高有一定的关系（190维）。
  目前看来，程序还有一些优化的地方：对于非参数估计的窗参数选择方面，还有很大的提升空间。非参数估计虽然程序运行耗时少，但是目前来看，分类性能却不及参数估计。如果修改非参数估计的窗（如修改Parzen窗的窗类型，窗的大小等），可能在分类正确率上还有提升空间。