贝叶斯分类器之统计决策方法和概率密度估计_专栏

一、前言

我们在之前的一篇文章中简单介绍了关于贝叶斯分类器的原理以及二分类的Matlab实现，这篇文章开始，我们将对贝叶斯分类器进行一个完整的剖析。本篇文章我们介绍统计决策方法和概率密度估计。
统计决策方法是基于概率论和数理统计的一种模式识别方法，主要方法有Bayes决策、聚类分析等。我们之前那篇文章介绍的是最小错误率Bayes决策，它使用类的条件概率和先验概率的乘积作为判别函数，将样本归到判别函数最大的一类中。在使用统计决策方法之前，我们首先需要进行概率密度估计。

二、概率密度估计

进行Bayes决策需要事先知道两种知识：类的先验概率和类的条件概率密度。

1.估计先验概率

我们在本篇文章中用训练数据中各类数据出现的频率，即训练数据中各类数据的占比来进行先验概率的估计，代码如下：

% 先验概率
pw1=n1/(n1+n2);
pw2=n2/(n1+n2);

2.类的条件概率密度估计

(1)参数估计

假设随机变量服从正态分布，正态分布的参数——均值和协方差矩阵通过训练数据确定，对每一个测试样本计算每一类的类的条件概率密度，结合先验概率得到判别函数，从而进行分类。
a.均值和协方差矩阵的估计
代码如下：

function [miu,sigma]=ParamerEstimation(Training_class)
    [~,n]=size(Training_class);
    miu=mean(Training_class,2);
    sigma=0;
    for i=1:n
        x=Training_class(:,i);
        sigma=sigma+(x-miu)*(x-miu)';
    end
    sigma=sigma/n;
end

b.通过估计的参数，得到类的条件概率密度（服从正态分布）
代码如下：

function y=gaussian(miu,sigma,x)
    d=size(miu,1);
    % 因为多分类中某些类估计出的协方差矩阵不可逆，加一个小的扰动矩阵可以避免计算错误
    I=5*eye(d);
    d=d/2;
    sigma=sigma+I;
    y=exp(-0.5*(x-miu)'*inv(sigma)*(x-miu))/sqrt(det(sigma));
end

(2)非参数估计

参数估计需要事先假定随机变量服从某种分布，而非参数估计不用进行任何模型假设，主要方法有：直方图法，Parzen窗法和近邻法。本篇文章将实现Parzen窗法和近邻法，直方图法读者可以自己尝试编写一下作为练习。
a. Parzen窗法
窗类型我们使用方窗。根据Parzen窗的原理，以x点为中心，固定超立方体的体积，计算落入超立方体中样本点的个数。如图，假设数据为二维，固定正方形窗的面积（平面体积），以x点为中心，统计落入窗里的点个数。最后根据图中公式，估计出类的条件概率密度。编程这里有一个简单的处理：先找出这个点坐标中的最大值，然后将最大值与方窗边长的二分之一进行对比，若最大值小于边长的二分之一，则说明这个点在窗内。

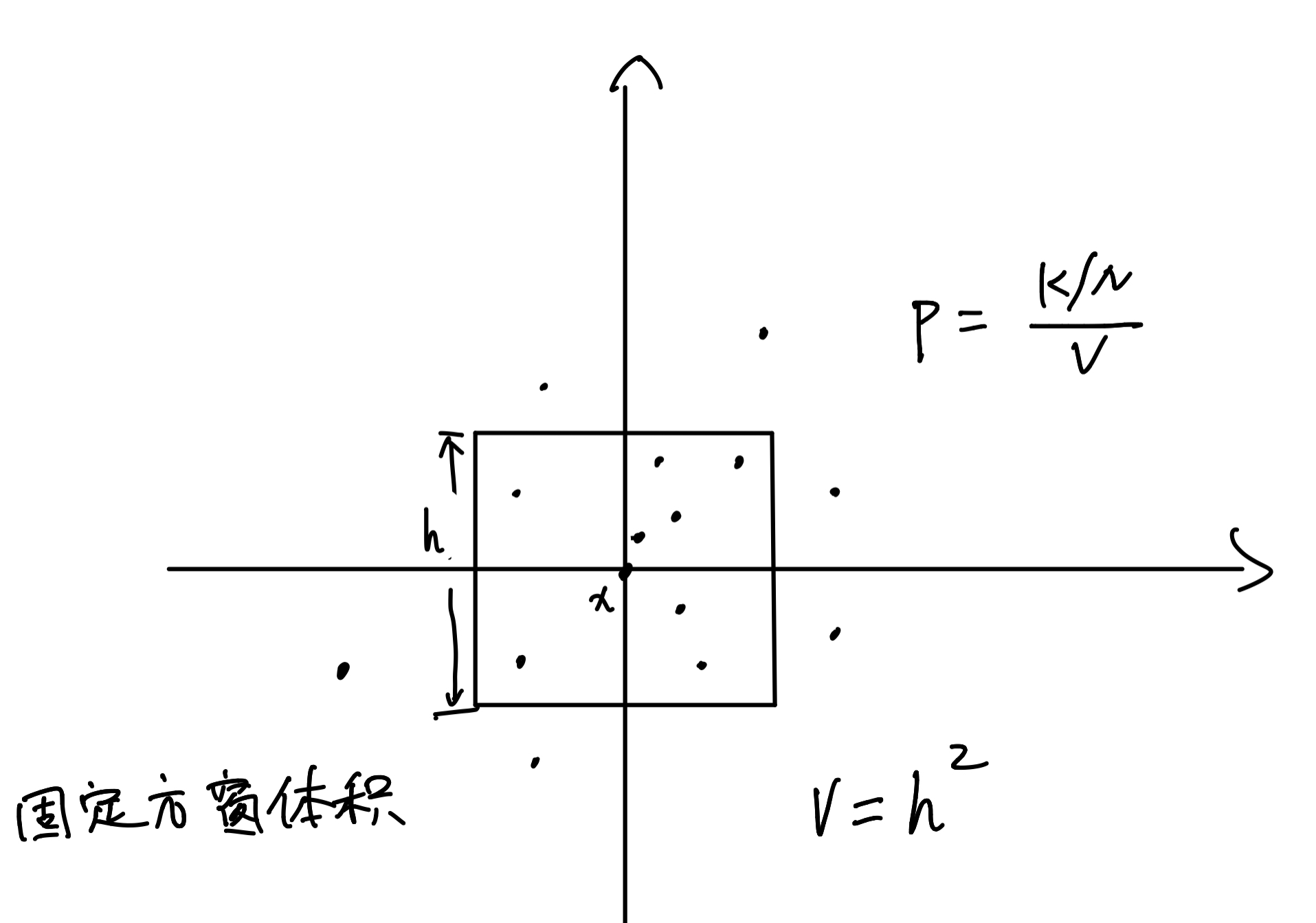
代码如下：

function p=Parzen(x,h,data)
    [d,n]=size(data);
    p=1;% 初始的p为落入窗中点的个数，算上中心点x，所以p的初始值等于1
    v=h^d;
    for i=1:n
        temp=abs(data(:,i)-x);
        max_distance=max(temp);
        if(max_distance<=h/2)
            p=p+1;
        end
    end
    p=p/(n*v);% 计算概率
end

b. 近邻法
按照近邻法的原理，以x点为中心，固定超立方体中点的个数sk，计算包含sk个点的超立方体的体积，以二维平面为例，如图所示：

和Parzen窗法类似，找出每个样本到x点距离最远的一维，若这一维的距离小于超立方体边长的二分之一，则认为该样本在超立方体中。那么，最远的一维可以用来衡量样本相对于中心点x的远近，对这个“最远一维的距离”进行排序，则可以找到恰好包含N个样本的超立方体。
代码如下：

function p=KNN(x,sk,data)
    [d,n]=size(data);
    v=1;
    sk=sk-1;%除去中心点x
    temp=abs(data-x);% 求样本每个维度到x点的距离
    max_distance=max(temp);% 求出相对于x点最远一维的距离
    max_distance=sort(max_distance);%对max_distance数组进行按行升序排列
    v=max_distance(sk)^d;% 计算包含sk个点的超立方体的体积
    p=sk/(n*v);
end

三、总结

我们这篇文章介绍了什么是统计决策方法以及概率密度估计，并且用Matlab实现了几种估计类的条件概率密度的方法，包括参数估计法和非参数估计法中的parzen窗法和近邻法。之前那篇贝叶斯二分类算法的实现中使用的就是参数估计法，此外，我们将在接下来的文章中使用非参数估计法进行二分类，然后观察它们之间的差别。